Чтобы найти площадь: Как найти площадь прямоугольника? Ответ на webmath.ru

Содержание

Как найти площадь треугольника, формула

Оглавление

Время чтения: 4 минуты

703

Понятие площади

Определение

Площадью (S) геометрической фигуры именуется численная величина, характеризующая её размер.

В этом собственно и состоит понятие площади. У неё есть следующие два свойства:

Площадь равных геометрических фигур имеет одно и то же числовое значение;
Величина площади фигуры равняется сумме единичных площадей квадратов, на которые её можно разделить.

Пример 1.

Пусть у нас имеется прямоугольник в котором укладывается 7 клеток по вертикали и 12 по горизонтали. Это значит он будет иметь стороны a=7 и b=12.

Из рисунка видно, что S нашего треугольника это половина таковой у прямоугольника. Последняя вычисляется так \[\mathrm{S}_{\text {прям }}=\mathrm{a} * \mathrm{~b}\]. Чтобы узнать площадь треугольника, разделим \[\mathrm{S}_{\text {прям }}\] на 2, тогда получим:

Формула 1

\[S= (a*b)/2\].

Подставляем численные значения (7*12)/2 = 42.

Как найти площадь треугольника, если мы знаем его основание и высоту

Теорема

Площадь любого треугольника численно равняется половине произведения длины основания на высоту фигуры.

В нашем случае основанием считается сторона AB. Формула для S получается следующей:

Формула 2

\[S=(1/2)*AB*h \].

Доказательство:

Посмотрите рисунок. Из него ясно видно, что высота h делит ABC на 2 прямоугольных треугольника ACH и HCB.

По формуле (1) вычисление S каждого из них идёт так.

S(ACH) = (1/2)(AH)*h

S(HCB)=(1/2)(HB)*h

Чтобы вычислить площадь треугольника abc, нужно S(ACH) и S(HCB) сложить.

S=(1/2)(AH)*h+ (1/2)(HB)*h

Выносим (1/2) и h за скобки и получаем

(1/2)*h*(AH+HB)

Но AH+HB=AB, т. е.

S = (1/2)*AB*h, что и требовалось доказать.

Как видите, формулу площади треугольника получить и доказать достаточно легко.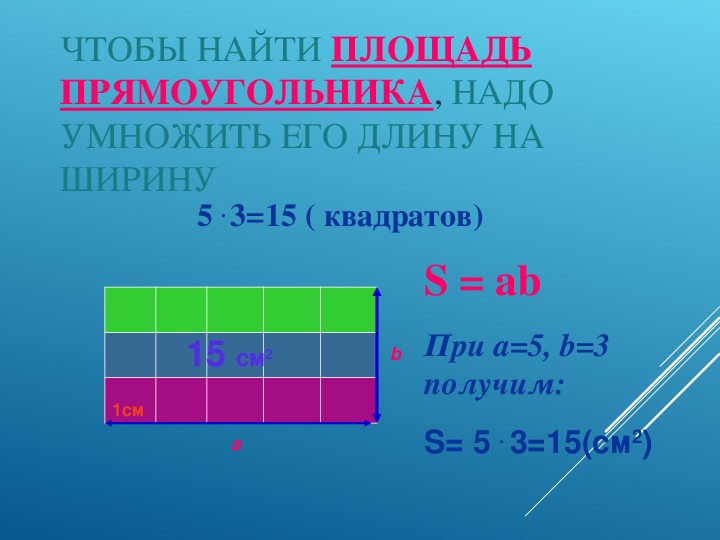 {2} \sqrt{3}}{4}\]

Что и требовалось доказать.

Оценить статью (0 оценок):

Как найти площадь фигуры

Площадь прямоугольника равна произведению длины и ширины смежных сторон. Площадь параллелограмма равна произведению основания и высоты. Площадь ромба равна половине произведения его диагоналей. Площадь треугольника равна половине произведения основания и высоты. Для нахождения площади фигуры, у которой разные стороны, можно использовать формулу S = a × h, где a — сторона, h — высота, или формулу S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

Некоторые свойства площади фигур

Содержание:

Как найти площадь в 4 классе?
Как найти площадь квадрата или прямоугольника?
Что такое площадь математика 5 класс?
Что такое площадь 2 класс?

Как найти площадь кривой фигуры 4 класс

Палетку используют для измерения площади фигур, ограниченных кривой линией.

Чтобы найти площадь данной фигуры, нужно:

На данную фигуру наложить палетку.
Сосчитать, сколько целых клеток- квадратных единиц — содержится в фигуре.
Сосчитать, сколько нецелых квадратных единиц содержится в фигуре.

Как найти площадь 4 класс

S = a × b, где S — площадь; a, b — длина и ширина.

Как найти площадь многоугольника

Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. Площадь первой фигуры равна сумме площадей двух маленьких фигур, из которых состоит эта фигура. Площадь второй фигуры равна сумме площадей трех маленьких фигур, из которых состоит эта фигура.

Как найти площадь и периметр фигур

Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = ( b) · 2, где P — периметр, — длина, b — ширина прямоугольника.

Как найти площадь в 4 классе

Чтобы найти площадь прямоугольника, надо длину умножить на ширину S = a× b .

Как найти площадь треугольника 4 класс пример

S пр = a ⋅ b . Поэтому для определения площади прямоугольного треугольника необходимо это произведение a ⋅ b разделить на 2. Чтобы найти площадь прямоугольного треугольника, нужно произведение его катетов разделить на 2.

Как найти площадь и периметр 4 класс

Как найти площадь квадрата или прямоугольника

Площадь прямоугольника равна произведению его длины и ширины: ・ . Площадь квадрата равна произведению двух его соседних сторон: ・ .

Как найти площадь прямоугольника

2) Для вычисления площади прямоугольника нужно умножить его длину на ширину. Формула для вычисления площади прямоугольника имеет следующий вид : S = a*b.

Как найти площадь квадрата в третьем классе

Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат. S = a × a = a2, где S — площадь, a — сторона. Эту формулу проходят в 3 классе.

Как найти Как найти площадь квадрата

Возведите длину стороны в квадрат.

Это все, что от вас требуется. Если длина сторон квадрата равна 3 см, то для вычисления площади квадрата нужно просто возвести ее в квадрат: 3 см x 3 см = 9 см2.

Как найти площадь прямоугольника 2 класс формула

Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника.

Как найти площадь прямоугольника 3 класс примеры

Чтобы найти площадь прямоугольника, надо найти произведение длин его сторон. 2 см ⋅ 4 см = 8 см 2 . Длина и ширина прямоугольника должны быть выражены (записаны) в одинаковых единицах длины.

Что такое площадь математика 5 класс

Площадь указывает на размер плоскости, которую занимает фигура. Если вырезать любую фигуру из листа бумаги, положить на поверхность, а потом обвести карандашом, мы получим визуальное воплощение характеристики площади. Площади двух абсолютно разных фигур могут быть одинаковыми.

Что такое площадь в математике пятый класс

Площадь — это плоскость внутри замкнутой геометрической фигуры.

Что такое площадь для детей

Когда мы говорим о площади, мы говорим о «части плоскости, заключённой внутри замкнутой геометрической фигуры», о том, сколько места занимает фигура на плоскости. Площадь находят мерками, квадратиками (поэтому и единицы площади квадратные — так детям понятнее).

Что такое площадь в математике формула

S = a × b, где a, b — длина и ширина прямоугольника. S = a × √(d2 — а2), где а — известная сторона, d — диагональ. Диагональ — это отрезок, который соединяет вершины противоположных углов. Она есть во всех фигурах, число вершин которых больше трех.

Что такое площадь первый класс

Площадь – это место, которое занимает фигура, периметр – длина границы фигуры. Периметр определяется числом отрезков – сторон клеток, ограничивающий квадрат и прямоугольник.

Что такое площадь для 2 класса

Площадь – свойство фигуры, занимать место на плоскости. Площадь – это внутренняя часть фигуры.

Что такое площадь 2 класс

Площадь – свойство фигуры, занимать место на плоскости. Площадь – это внутренняя часть фигуры.

Что такое площадь объяснение

Площадь — это плоскость внутри замкнутой геометрической фигуры.

Что такое площадь квадрата 2 класс

Площадь квадрата равна квадрату его стороны. Периметр квадрата равен сумме его четырех сторон.

Что такое площадь и что такое периметр

Периметр квадрата равен сумме длин всех его сторон. Площадь квадрата равна произведению длин двух его сторон. Периметр фигуры обозначают большой латинской буквой P, площадь — большой латинской буквой S, а стороны фигур — маленькими латинскими буквами , b и др.

Что такое площадь в математике 4 класс

Площадь-это свойство фигур занимать место на плоскости. Квадратный километр-единица измерения площади, равная площади квадрата со стороной 1м.

Что такое площадь в математике 3 класс

Площадь – внутренняя часть любой плоской геометрической фигуры. Квадрат – это прямоугольник, у которого все стороны равны. Прямоугольник – это четырёхугольник, у которого все углы прямые. Квадратный сантиметр – квадрат со стороной 1 сантиметр.

Как найти площадь квадрата? Формула, определение

Площадь квадрата можно понять по тому, сколько пространства занимает внутри него квадрат. Проще говоря, пространство, находящееся в пределах границы квадрата, известно как площадь квадрата. В этой статье вы узнаете основные параметры квадрата. Кроме того, вы узнаете, как найти площадь квадрата, площадь формулы квадрата и площадь поверхности квадратной пирамиды.

Все ли мы знаем, что такое квадрат? Квадрат – это замкнутый четырехугольник. Четырехугольники – это фигуры, имеющие 4 стороны. Таким образом, квадрат — это четырехсторонняя фигура, у которой все четыре стороны равны. Если одна сторона квадрата равна 10 см, то и другие стороны равны 10 см. Давайте сначала изучим некоторые математические термины и понятия, связанные с квадратом:

У квадрата все стороны равны. Отсюда следует, что противолежащая и прилежащая стороны квадрата равны друг другу.
Противоположные стороны квадрата параллельны, что делает его параллелограммом.
Смежные стороны квадрата перпендикулярны друг другу. Это означает, что любые две смежные стороны имеют между собой угол 90 градусов.
Квадрат разделен на два равных прямоугольных треугольника.
Квадрат — это частный случай прямоугольника.
Периметр квадрата: Расстояние, пройденное границами квадрата, называется периметром квадрата. Он сформулирован как:

Периметр (квадрат) = s + s + s + s = 4 x s = 4s {где s — сторона квадрата}

В нашей повседневной жизни мы можем встретить квадраты повсюду. От наших домов до наших школ квадраты присутствуют на каждом углу. Плитка на вашей кухне квадратная. Шахматная доска представляет собой квадрат, состоящий из 64 черных и белых меньших квадратов. Самый распространенный пример — кубик Рубика. Каждая поверхность кубика Рубика квадратная.

Другие измерения, такие как диагональ и периметр квадрата, также могут использоваться для вычисления площади квадрата. В этой статье мы попытаемся узнать больше о площади квадрата.

Площадь квадрата

Площадь квадрата определяется как количество квадратных единиц, необходимых для заполнения этой формы. Другими словами, при вычислении площади квадрата мы учитываем длину его стороны. Поскольку все стороны фигуры равны, ее площадь равна произведению двух сторон. Наиболее распространенными единицами измерения площади квадрата являются квадратные метры, квадратные футы, квадратные дюймы и квадратные сантиметры.

Площадь квадрата также можно вычислить, используя другие измерения, такие как диагональ и периметр квадрата. На этой странице мы попытаемся узнать больше о площади квадрата.

Какова площадь квадрата?

Квадрат — это двумерная замкнутая фигура, имеющая четыре равные стороны и четыре равных угла. Четыре угла при вершинах образованы четырьмя сторонами квадрата. Периметр квадрата — это сумма длин всех его сторон, а площадь квадрата — это площадь, занимаемая фигурой. Он обладает следующими свойствами четырехугольника.

Две стороны параллельны.

Все четыре стороны одинаковые.
Все углы 90 ^o .

Квадраты можно найти повсюду. Вот несколько примеров часто встречающихся объектов квадратной формы. Квадрат представлен шахматной доской, часами, доской и плиткой.

Иллюстрация: Рассмотрим квадрат длины 4 единицы. Теперь рассмотрим меньшие квадраты длиной 1 единица каждый. Как мы видим на рисунке ниже, 4 квадрата по 1 единице заполняют первый ряд большего квадрата. Точно так же по 4 квадрата 1 единицы заполняют второй, третий и четвертый ряд. Теперь большой квадрат заполнен.

Из этого мы можем сделать вывод, что площадь квадрата равна произведению двух его сторон. Как мы знаем, 16 = 4 х 4, а 4 единицы составляют одну сторону квадрата. В следующем разделе мы изучим и выведем формулу площади квадрата.

Формула площади квадрата

Из приведенного выше рисунка мы узнаем, что площадь квадрата равна произведению сторон. Это можно записать как «сторона х сторона». Следовательно, формула для любого квадрата с любой длиной стороны задается как

Площадь = (Сторона) ²

Давайте рассмотрим пример, чтобы понять эту формулу:

Пример: Найдите площадь квадрата со стороной 13 см.

Решение: При длине стороны = 13 см

Площадь квадрата = (Сторона) ² = (13) ² = 169 см ² .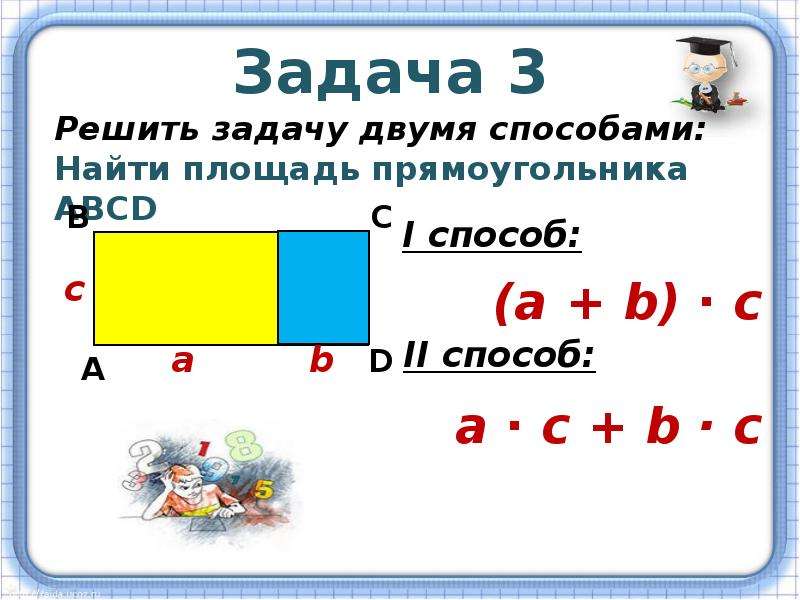

Площадь квадрата всегда выражается в квадратных единицах (квадратный сантиметр, квадратный метр, квадратный дюйм и т. д.)

Что если нам даны не стороны квадрата, а длина диагонали? Как найти площадь квадрата в этом случае?

Не волнуйтесь! Площадь квадрата можно вычислить, даже если известна длина диагонали. Вы можете найти площадь, используя формулу, написанную ниже:

Площадь квадрата (с использованием диагоналей) = (D) ² /2, где D представляет собой длину диагонали.

Примечание: Помните, что диагонали квадрата равны, поэтому площадь остается неизменной, если дана любая из диагоналей.

Пример: Найдите площадь квадрата, если длина диагонали равна 13 см.

Решение: Дано, диагональ = 13 см

Площадь квадрата = D = (13) ² /2

= 169/2 см ²

Как найти площадь квадрата

До сих пор мы выучили 2 формулы, связанные с нахождением площади квадрата. Давайте узнаем, как вы будете подходить к вопросам, связанным с площадью любого квадрата.

1.

Когда дана чья-либо сторона:

Шаг 1: Запишите значение стороны, скажем «а».
Шаг 2: Подставьте значение an в формулу -> Площадь (со стороной) = (Сторона) ² = (a) ²
Шаг 3: Запишите ответ в квадратных единицах.

Пример: Найдите площадь пластика, необходимую для покрытия квадратного стола длиной 8 м.

Решение: Учитывая, что длина стола = 8 м

Поэтому площадь пластика, необходимая для покрытия стола, = площади стола.

Площадь стола = (сторона) ² = 8 ² = 64 м 45

Шаг 1: Запишите значение диагонали длина, скажите «d».
Шаг 2: Подставляем значение d в формулу -> Площадь (с диагональю) = (d) ²/2 =
Шаг 3: Запишите результат в квадратных единицах.

Пример: Найдите площадь квадрата с диагональю 4 см

Решение: Учитывая, что длина диагонали = 4 см 2 /2 = 16/2 = 8 см ²

Найдите площадь квадрата, зная периметр квадрата

В предыдущих разделах мы научились вычислять площадь квадрата, зная сторону или диагональ. Но, предположим, вам не предоставлен ни один из этих параметров, но задан периметр квадрата. Как найти площадь, если известен периметр квадрата? Давайте узнаем:

Шаг 1: Запишите периметр данного квадрата.
Шаг 2: Мы знаем, что периметр квадрата равен 4 с. Следовательно, 4s = периметр.
Шаг 3: Подставьте значение периметра и найдите сторону по формуле s = Периметр/4
Шаг 4: Теперь мы знаем сторону квадрата. Найдите площадь, используя s2.
Шаг 5: Запишите ответ в квадратных единицах.

Пример: Квадратный сад имеет периметр 64 см. Макс хочет посадить цветы и найти площадь этого сада, но не знает, как это сделать? Помогите ему определить площадь сада.

Решение: Мы знаем: Периметр сада = 64 см

Сначала вычислим длину сторон сада.

Используя формулу из шага 3

Сторона (s) = периметр/4

= 64/4

= 16 см

Теперь,

Площадь сада = (s) ²

= 16 ²

Несколько советов с нашей стороны:

Обратите внимание на следующие факторы, которые следует учитывать иметь в виду, когда вы вычисляете площадь квадрата.

При вычислении площади квадрата мы часто ошибаемся, удваивая число. Это не вариант! Имейте в виду, что площадь квадрата не равна удвоенной стороне. Это всегда либо «сторона х сторона», либо сторона ² .

Мы должны помнить о единицах измерения площади при ее представлении. Площадь квадрата всегда двумерна; следовательно, мы используем квадратные единицы. Например см ² , м ² , дюйм ² и т. д.

Часто задаваемые вопросы

1. Что такое площадь квадрата в геометрии?

Площадь квадрата в геометрии — это измерение поверхности. Он рассчитывается путем умножения длины на ширину.

2. Что такое формула площади квадрата?

Формула площади квадрата позволяет вычислить площадь квадрата. Формула площади квадрата: A = s2, где s представляет длину каждой стороны квадрата.

3. Как вычислить площадь квадрата?

Чтобы вычислить площадь квадрата, нужно длину одной стороны умножить на саму себя. Итак, если у вас есть квадрат со сторонами по 10 сантиметров, вы должны сделать: 10 * 10 = 100.

4. Каковы единицы измерения площади квадрата?

Единицами площади квадрата являются квадраты. Наиболее распространенной единицей измерения площади являются квадратные метры, но иногда вы также можете встретить квадратные футы или акры.

5. Что такое периметр и площадь квадратных формул?

Формула для периметра квадрата: p = 4s

Формула площади квадрата: A = s ²

1.3: Рассуждение для нахождения площади

Последнее обновление
Сохранить как PDF

Идентификатор страницы
39429

Иллюстративная математика
OpenUp Resources

Lesson

Давайте разложим и переставим фигуры, чтобы найти их площади.

Упражнение \(\PageIndex{1}\): Сравнение регионов

Является ли площадь рисунка A больше, меньше или равна площади заштрихованной области на рисунке B? Будьте готовы объяснить свои рассуждения.

Упражнение \(\PageIndex{2}\): На сетке

Каждый квадрат сетки равен 1 квадратной единице. Найдите площадь в квадратных единицах каждой заштрихованной области, не считая всех квадратов. Будьте готовы объяснить свои рассуждения.

Готовы ли вы к большему?

Переставьте треугольники с рисунка C так, чтобы они поместились внутри рисунка D. Нарисуйте и раскрасьте схему своей работы.

Упражнение \(\PageIndex{3}\): вне сети

Найдите площадь заштрихованных областей каждой фигуры. Объясните или покажите свои рассуждения.

Резюме

Разложить его на фигуры, площади которых вы умеете вычислять; найдите площадь каждой из этих фигур, а затем добавьте площади.

Разложите его и переставьте части в формы, площадь которых вы умеете вычислять; найдите площадь каждой из этих фигур, а затем добавьте площади.

Рассматривайте это как фигуру с отсутствующей частью; вычислите площадь фигуры и недостающей части, а затем вычтите площадь части из площади фигуры.

Площадь рисунка всегда измеряется в квадратных единицах. Когда длины обеих сторон прямоугольника даны в сантиметрах, то площадь дана в квадратных сантиметрах. Например, площадь этого прямоугольника равна 32 квадратных сантиметра.

Записи глоссария

Определение: Площадь

Площадь — это количество квадратных единиц, покрывающих двумерную область без каких-либо промежутков или перекрытий.

Например, площадь области А составляет 8 квадратных единиц. Площадь заштрихованной области B равна \(\frac{1}{2}\) квадратной единицы.

Определение: Compose

Compose означает «собрать воедино». Мы используем слово составить , чтобы описать объединение более чем одной фигуры для создания новой формы.

Определение: Разложить

Разложить означает «разобрать». Мы используем слово , разложить , чтобы описать разбивание фигуры на части для создания более чем одной новой формы.

Определение: область

Область — это пространство внутри фигуры. Некоторые примеры двумерных областей находятся внутри круга или внутри многоугольника. Некоторыми примерами трехмерных областей являются внутренняя часть куба или внутренняя часть сферы.

Практика

Упражнение \(\PageIndex{4}\)

Найдите площадь каждой заштрихованной области. Покажите свои рассуждения.

Упражнение \(\PageIndex{5}\)

Найдите площадь каждой заштрихованной области. Покажите или объясните свои рассуждения.

Упражнение \(\PageIndex{6}\)

Два земельных участка очень разной формы. Ной сказал, что оба участка земли имеют одинаковую площадь.

Вы согласны с Ноем? Объясните свои рассуждения.

Упражнение \(\PageIndex{7}\)

Домовладелец решает, какой размер плитки использовать для полной облицовки прямоугольной стены в ванной комнате размером 80 на 40 дюймов. Плитки представляют собой квадраты с тремя длинами сторон: 8 дюймов, 4 дюйма и 2 дюйма. Укажите, согласны ли вы с каждым утверждением о плитках. Объясните свои рассуждения.

Независимо от того, какой размер она выберет, ей понадобится одинаковое количество плиток.
Независимо от размера, который она выбирает, площадь стены, которая выкладывается плиткой, одинакова.
Ей понадобятся две 2-дюймовые плитки, чтобы покрыть ту же площадь, что и одна 4-дюймовая плитка.
Ей понадобится четыре 4-дюймовых плитки, чтобы покрыть ту же площадь, что и одна 8-дюймовая плитка.
Если она выберет 8-дюймовые плитки, ей понадобится в четыре раза меньше плиток, чем 2-дюймовых плиток.