В цилиндрический сосуд налили
Друзья! В заданиях ЕГЭ по математике встречаются задачи, в которых речь идёт о погружении детали в жидкость или о переливании жидкости из одного сосуда в другой. Вопросы в условии связаны с нахождением объёма погружаемого в жидкость тела или с нахождением какого-либо параметра сосуда. Форма сосуда может быть различной: цилиндр, призма.
Что необходимо понимать? Если жидкость залита в цилиндрический сосуд, то она принимает форму цилиндра. Если она залита в имеющий форму призмы, то соответственно принимает форму призмы. Это означает, что формулы для объёмов цилиндра и призмы работают и для объёмов жидкостей помещённых в такие сосуды.
Формула объёма цилиндра (и призмы):
Если жидкость переливается в аналогичный сосуд с меньшим основанием, уровень (высота) жидкости увеличивается; если в сосуд с большим основанием, то уровень жидкости уменьшается.
Рекомендации!
В задачах на погружение детали в жидкость следует найти объём полученный после её погружения, далее найти разность объёмов до и после (если данные в условии это позволяют).
Можно такие задачи решать и другим способом, используя закон Архимеда. Примеры рассмотрены ниже.
В задачах, где идёт речь о переливании жидкости в другой сосуд (с уменьшенной или увеличенной площадью основания) помните о том, что сам объём жидкости остаётся неизменным. Вы можете выразить его через площадь основания и высоту (S1 и H1) одного сосуда и площадь основания и высоту (S2 и H2) другого сосуда, далее полученные выражения приравнять.
При дальнейших преобразованиях получите отношение соответствующих величин – либо площадей оснований, их рёбер, либо высот. Пример такой задачи рассмотрен ниже в статье.
Можно такие задачи решать и другим способом, используя закон Архимеда. Примеры рассмотрены ниже.В цилиндрический сосуд налили 5000 см3 воды. Уровень жидкости оказался равным 40 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 15 см. Чему равен объем детали? Ответ выразите в см3.
Мы знаем, что объём цилиндра равна произведению площади основания на высоту:
В жидкость погружаем деталь.
Её уровень поднимается. Для того, чтобы вычислить объём детали необходимо из полученного объёма (полученного после погружения детали) вычесть объём жидкости, который был изначально.
Высота это есть уровень жидкости.
Итак, из имеющихся данных можем найти площадь основания:
Основание цилиндра у нас величина неизменная, но изменилась высота жидкости (при погружении детали) на 15 сантиметров, то есть она стала
40 +15 = 55 см.
Найдём полученный объём:
Теперь можем вычислить объём детали: 6875 – 5000 = 1875 см3
Можно решать подобные задачи более рациональным способом.
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 15/40 исходного объема:
Ответ: 1875
Решить самостоятельно:
Посмотреть решение
В сосуд, имеющий форму правильной треугольной призмы, налили 2500 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 20 см до отметки 24 см.
Чему равен объем детали? Ответ выразите в см3.
Принцип решения тот же самый, что и в предыдущей задаче.
Мы знаем, что объём призмы равен произведению площади основания на высоту:
В жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы вычислить объём детали необходимо из полученного объёма (полученного после погружения детали) вычесть объём жидкости, который был изначально.
Из имеющихся данных можем найти площадь основания призмы:
Основание призмы не изменилось, но изменилась высота жидкости (при погружении детали) она стала 24см.
Найдём полученный объём:
Теперь можем вычислить объём детали: 3000 – 2500 = 500 см3
Второй способ:
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 4/20 исходного объема:
Ответ: 500
Решить самостоятельно:
Посмотреть решение
В сосуд, имеющий форму правильной треугольной призмы, налили воду.
Уровень воды достигает 250 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 5 раз больше, чем у первого? Ответ выразите в см.
В подобных задачах с переливаниями жидкости следует помнить, что объём её остаётся прежним (он не изменен – куда бы её не перелили).
Объем жидкости в данном случае это объём правильной треугольной призмы (в её основании лежит правильный треугольник). Он равен произведению площади основания призмы на высоту:
Суть дальнейших действий сводится к тому, что мы можем выразить объёмы жидкостей в двух призмах: первой и второй (основание которой в 4 раза больше), а затем приравнять полученные выражения, в итоге после преобразований получим отношение двух высот.
Естественно, что высота жидкости уменьшится, если увеличить площадь основания.
Обозначим исходную высоту жидкости Н1, полученную после переливания Н2.
Найдём площадь основания призмы, обозначив его сторону как а.
Площадь правильного треугольника равна:
Таким образом, объём залитой жидкости в первую призму равен:
Площадь основания второй призмы равна:
Объём залитой жидкости во вторую призму равен:
Найдём отношение высот:
Таким образом, при том же объёме жидкости её высота уменьшится в 25 раз и будет равна 10.
Или можно сказать так:
При увеличении стороны основания а в 5 раз уровень воды уменьшится в 25 раз.
Ответ: 10
Решить самостоятельно:
Посмотреть решение
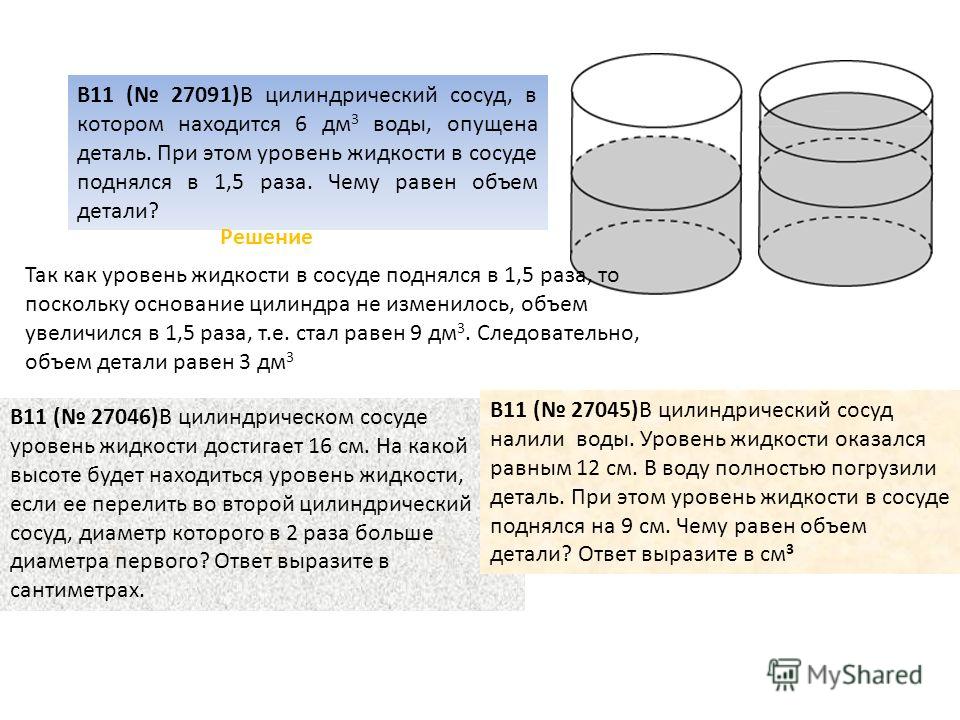
В цилиндрический сосуд, в котором находится 14 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,1 раза. Чему равен объем детали? Ответ выразите в литрах.
Объём цилиндра равна произведению площади его основания на высоту:
Жидкость в сосуде имеет цилиндрическую объёмную форму.
Уровень жидкости поднялся в 1,1 раза – означает, что высота цилиндра увеличилась в 1,1 раза.
Исходя из формулы объёма цилиндра понятно, что при увеличении высоты в 1,1 раза влечёт за собой увеличение объёма также в 1,1 раза (так как зависимость величин прямопропорциона).
Это означает, что после погружения детали объём будет равен 14∙1,1 = 15,4 литра.
Таким образом, объём детали будет равен: 15,4 – 14 = 1.4 литра.
Ответ: 1,4
Решить самостоятельно:
Посмотреть решение
Если ход решения сразу не увидели, ставьте вопрос – что можно найти исходя из условия?
Например, если дан начальный объём и высота жидкости (в сосуде формы призмы или цилиндра), то мы можем найти площадь основания. Затем, зная площадь основания и высоту жидкости после погружения детали мы можем найти объём.
Далее вычислить разницу между объёмами не составит труда (это относится к первым двум задачам). В последней задаче для решения требуется немного логики.
В задачах по стереометрии на ЕГЭ есть много таких, где требуется найти изменение объёма или площади поверхности (шара, призмы, куба, пирамиды, конуса), при изменении одного из линейных размеров, имеются задачи и обратные им.
В данной рубрике мы рассмотрим такие задачи, не пропустите!
На десерт видео, отдохнём от математики.
Успехов вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
формулы для расчета, пояснения, примеры / Справочник :: Бингоскул
Все замечали, что разные вещества, занимающие один объем, весят по-разному. Ведёрко воды весит меньше, чем песка или камней. Вес тела зависит от его плотности – концентрации вещества в единице объема. Рассмотрим связь между этими величинами, способы, как найти массу воды в физике, зная её объём.
Что такое плотность
Плотностью называется скалярная величина, определяющаяся как отношение массы вещества к занимаемому им объёму. Плотность – величина не постоянная, поэтому для многих веществ берётся усреднённое значение, измеренное в нормальных условиях. Так, например, плотность многих встречаемых в повседневной жизни тел зависит от внешних условий.
Если говорить о зерне, древесине, грунте, песке, их единица объёма весит тем больше, чем вещество влажнее – в нём больше влаги.
На плотность жидкостей заметное влияние оказывает температура: при охлаждении концентрация в единице объёма увеличивается, при нагревании вещество становится менее плотным.
Здесь есть исключения – вода. Её вес, вязкость достигают пика при температуре 4 °C, при охлаждении и нагревании они снижаются. Лёд получается легче, чем вода, поэтому он образовывается на поверхности водоёмов, на дно не опускается.
При измерении плотности пористых, сыпучих материалов указывается его:
- Насыпное значение – реальное, измеряемое без учёта пустот. Например, сыпучие крупы, щебень, известняк.
- Истинное – от занимаемого объёма отнимаются пустоты. Они определяются практическим путём, например, погружением тела в воду, или через ранее вычисленные коэффициенты.
Плотность при переходе вещества между фазовыми состояниями обычно изменяется скачкообразно, наибольшая разница наблюдается при испарении твёрдых веществ – сублимации.
Формула массы жидкости
Плотность в физике обозначается буквой греческого алфавита , измеряется в кг/м3. Зависит от массы тела и объёма, который занимает:
ρ= m : V, где:
- m – масса тела;
- V – объём.
Все ли знают, как найти массу газа через давление и занимаемый им объем? Для этого пользуются формулой Клапейрона-Менделеева:
pV = (m : M) * RT, где:
- p – давление газа;
- M и T– его молярная масса и температура;
- R – постоянная, равняется 8,314 Дж/(моль⋅К).
Для вычисления массы необходимо провести ряд математических операций: разделим обе части уравнения на ρV, затем – умножим на m, получим:
m = pVM : RT.
Рассмотрим, как найти объем детали, погруженной в жидкость, используя приведённую формулу.
Задачи
В ведро цилиндрической формы налили 5 л воды. Её уровень составил 0,4 м. После погружения в ведро тела уровень жидкости поднялся до 0,55 м.
Определите его объём.
Дан объём воды: 5 л или 5000 см3, остальные величины переведём в сантиметры для простоты вычислений: 40 см, 55 см.
Объём цилиндра вычисляется по формуле: V = Sосн * H. Найдём площадь основания:
Sосн = V : H = 5000 : 40 = 125 см2.
Далее вычисляем занимаемый водой и деталью объём:
V = Sосн * H = 125 * 55 = 6875 см3.
Высчитываем разницу: 6875 – 5000 = 1875 см3.
Далее рассмотрим, как найти массу жидкости, зная её вес, объём.
Вычислим вес 5-литровой бутыли подсолнечного масла.
Объём известен – 0,005 м3, плотность подсолнечного масла принимают за 920 кг/м3.
Подставим значения в формулу:
m = V * ρ = 0,005 * 920 = 4,6 кг.
Плотность и плавучесть
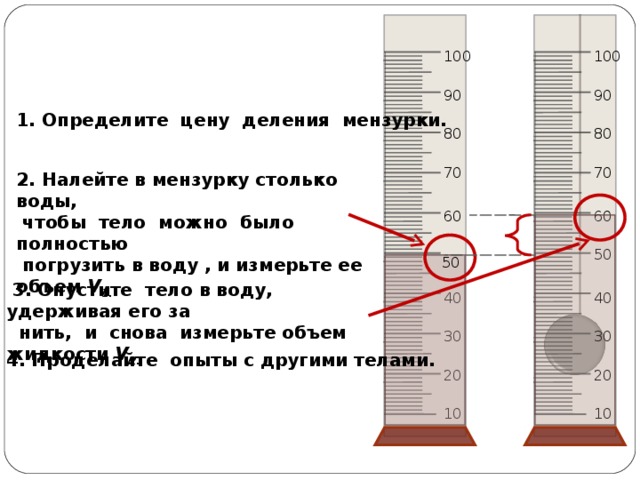
Цели:
Изучить методы измерения плотности
- жидкости и твердые вещества правильной формы прямым измерением массы и объема
- твердые вещества непрямым измерением объема
- жидкости и твердые тела неправильной формы (например, образцы минералов) с использованием принципа Архимеда.
Ознакомиться с измерительными приборами и оценкой погрешности измерений.
Введение
Масса — это физическое свойство, которым обладают все объекты, но объекты одного размера могут иметь разную массу и вес. Эта разница характеризуется другим свойством — плотностью. Плотность определяется как отношение массы объекта к его объему:
| . , где d — плотность жидкости, g — ускорение свободного падения и v — объем погруженного тела (или погруженной части тела, если оно поплавки). В этом эксперименте чашечные весы будут сравнивать массы в граммах, а не веса. Поскольку W=mg, видимое изменение массы при погружении составляет
Принцип Архимеда будет использоваться в этом эксперименте двумя способами:
Используйте конверты для хранения металлических цилиндров с их именами, если лаборатория растягивается на два дня, чтобы им не пришлось заново измерять цилиндр. Калькулятор плавучестиСоздано Bogna Szyk Отзыв Стивена Вудинга Последнее обновление: 13 мая 2022 г. Содержание:
Этот калькулятор плавучести представляет собой простой инструмент, который позволяет вам определить выталкивающую силу в мгновение ока. Если вам интересно, как рассчитать выталкивающую силу вручную, не беспокойтесь — мы вам поможем! Что такое выталкивающая сила?Плавучесть, иначе называемая выталкивающей силой , представляет собой силу, действующую в направлении, противоположном силе тяжести, которая предотвращает погружение плавучего объекта. Когда объект погружается в воду (или любую другую жидкость), его вес тянет его вниз. Плавучесть противостоит этому весу и имеет величину, прямо пропорциональную объему жидкости, которая в противном случае занимала бы пространство, занимаемое объектом, — другими словами, объему вытесненной жидкости. Еще одна ситуация, в которой вы можете наблюдать явление плавучести, это когда объекты менее плотные, чем воздух, плавают над землей. Пожалуйста, взгляните на наш калькулятор гелиевых шаров для особых случаев
Наш калькулятор плавучести имеет значение по умолчанию для ускорения свободного падения, равное 9,81 м/с². Если вы хотите изменить это значение, откройте Как рассчитать выталкивающую силуЕсли вы хотите найти выталкивающую силу с пошаговые расчеты вместо использования нашего калькулятора плавучести следуйте инструкциям ниже:
Часто задаваемые вопросыЧто такое единица плавучести в системе СИ?Единицей выталкивающей силы в системе СИ является Ньютон (Н) . Один ньютон — это сила, необходимая для ускорения из состояния покоя тела массой 1 кг на 1 метр в секунду. Что вызывает плавучесть?Давление жидкости увеличивается с ее глубиной. Это возрастающее давление жидкости вызывает направленную вверх силу для сброса давления, которую мы называем выталкивающей силой. Какая плавучесть мне нужна, чтобы не утонуть? Вам потребуется около 30-50 ньютонов выталкивающей силы, чтобы не утонуть. Как измерить объем тела с помощью плавучести?Чтобы оценить объемы тела дома:
Как оценить плавучесть 1-литровой бутылки с водой? Мы оцениваем плавучесть, необходимую для объекта, используя формулу |
Выталкивающая сила может быть выражена как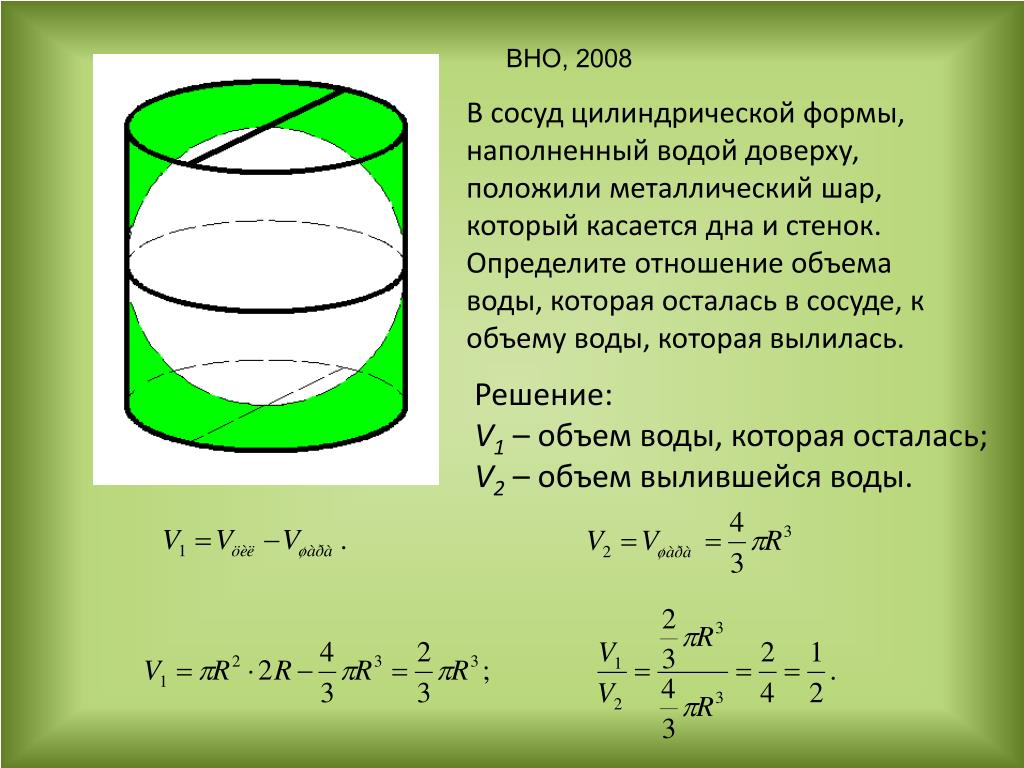
Найдите разницу между фактической и кажущейся массами и сравните ее с массой вытесненной воды, используя соотношение (3).
Определите массу сухого градуированного цилиндра, а затем заполните его примерно наполовину неизвестной жидкостью.
Все, что вам нужно сделать, это указать плотность жидкости и объем объекта, который остается под водой, и он будет использовать формулу плавучести для оценки силы, удерживающей объект на плаву.
Например, допустим, он равен 0,03 м³.
Вот почему спасательные жилеты обеспечивают плавучесть более 33 Н, которая увеличивается с увеличением веса человека.