Разработка урока «Определение наибольшего объема коробки» по теме «Компьютерные модели»
МЕТОДИЧЕСКАЯ ИНФОРМАЦИЯ
Название образовательной программы
Авторская программа курса информатики и информационных технологий для 5-7 классов лицея № 4 г. Краснодара Коротенко А. А, разработанная на основе обязательного минимума содержания образования по информатике (уровень Б) и учебного плана МОУ-лицей № 4 города Краснодар.
Тип урока
Практическая работа: «Определение наибольшего объема коробки» по теме «Компьютерные модели» для учащихся 6 класса
Цели урока
Обучающая – научить анализировать текст задачи, разбивать решение задачи на этапы, применять на практике полученные знания, научить проводить компьютерный эксперимент, использовать для решения задачи графики и диаграммы.
Развивающая – учить анализировать полученные результаты, сравнивать, делать выводы.
Воспитательная
Задачи урока
- Выполнить постановку задачи «Определение наибольшего объема коробки».
- Разработать математическую модель решения.
- Выполнить компьютерную реализацию модели.
- Провести компьютерный эксперимент.
- Проанализировать результаты и сделать выводы.
Ожидаемые результаты
В ходе урока ученики актуализируют знания, приобретенные при изучении тем «Моделирование», «Компьютерное моделирование», приобретут практические навыки в решении задачи путем разбиения процесса решения на этапы, в том числе: в проведении компьютерного эксперимента и анализе полученных результатов, закрепят знания о назначении, целесообразности и смысле компьютерного моделирования.
ПОДРОБНЫЙ КОНСПЕКТ УРОКА
Мотивация учащихся
Раздел «Моделирование» является интересным, но непростым для понимания и усвоения в школьном курсе информатики.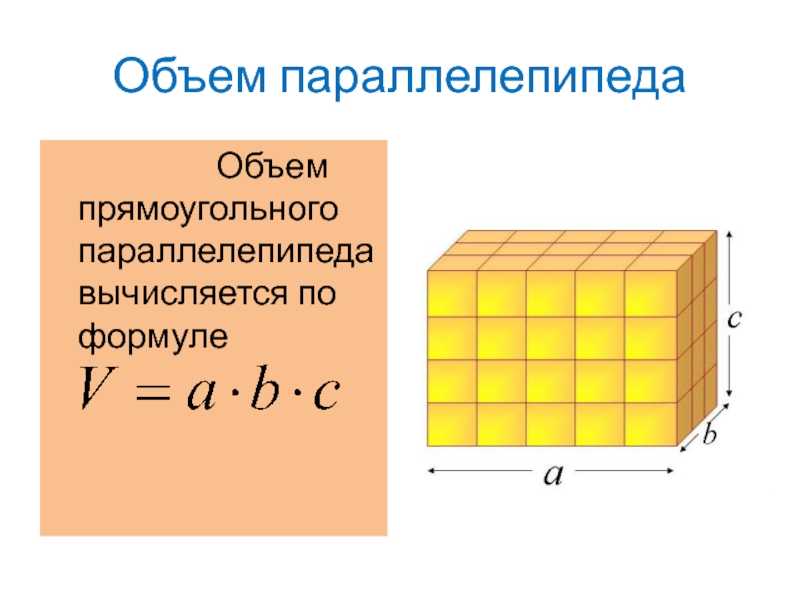 Рассматриваемый урок является логическим продолжением изучения теоретического материала по теме «Компьютерное моделирование» и содержит Практическую работу, назначение которой: в процессе решения несложной задачи рассмотреть все этапы построения и применения компьютерной модели и добиться от каждого ученика полного выполнения и усвоения предложенного материала.
Рассматриваемый урок является логическим продолжением изучения теоретического материала по теме «Компьютерное моделирование» и содержит Практическую работу, назначение которой: в процессе решения несложной задачи рассмотреть все этапы построения и применения компьютерной модели и добиться от каждого ученика полного выполнения и усвоения предложенного материала.
Цель решения задачи доступна для понимания учащимися 6 класса. Математическая модель решения задачи знакома учащимся из курса математики. Во время объяснения учитель использует презентацию, которая содержит цель работы, повторение необходимого теоретического материала, задание на текущий урок, домашнее задание. Учитель организует совместное обсуждение работы с учащимися в форме диалога. На этапе формализации и постановки задачи применяется раздаточный материал – бумажные модели (развертки) прямоугольных параллелепипедов, выполненные из квадрата заданного размера, но с различной величиной выреза для того, чтобы учащиеся могли 
Учащиеся понимают, что цель урока – создать компьютерную модель, провести эксперимент и проанализировать результаты. Для большей наглядности можно использовать графики и диаграммы. Результаты трех компьютерных экспериментов учащиеся будут заносить в таблицу.
Ход и содержание урока
I. Объявление темы, целей и задач урока
II. Актуализация опорных знаний
Учитель предлагает ученикам вспомнить, что такое моделирование и модель, виды моделей. Повторить понятия формализации, обсудить: какая задача считается «хорошо поставленной»? Учащиеся повторяют этапы решения задачи на компьютере. Раскрывают понятие «адекватности модели». Учитель подводит учеников к выводу о том, что существуют ситуации, когда компьютерное моделирование является единственно возможным способом решения поставленной задачи.
III. Объяснение содержания и выполнение практической работы – презентация
Сформулируем задачу. Из квадратного листа металла необходимо сделать коробку наибольшего объема. [1]
Из квадратного листа металла необходимо сделать коробку наибольшего объема. [1]
Некоторые из вас, ребята, ошибочно полагают, что какую бы форму не имела коробка, сделанная из одного и того же листа, её объём будет постоянным. От чего же зависит объём коробки? Можем ли мы позволить себе взять несколько листов металла и наугад выкраивать коробки? Каким образом мы убедимся, что полученная коробка будет иметь наибольший объём? Очевидно, что нам поможет компьютерное моделирование.
Этап 1. Постановка задачи
Дано: квадрат со стороной а см. По углам вырезаются квадраты со стороной b см. Найти: величину выреза b такую, чтобы объем коробки был наибольшим.
Этап 2. Построение математической модели
Нам необходимо найти объем прямоугольного параллелепипеда. Воспользуемся известной формулой V=a*b*c. Заметим, что в качестве расчетной формулы мы могли бы использовать другие алгебраические выражения, но была бы при этом модель адекватной? Доработаем модель.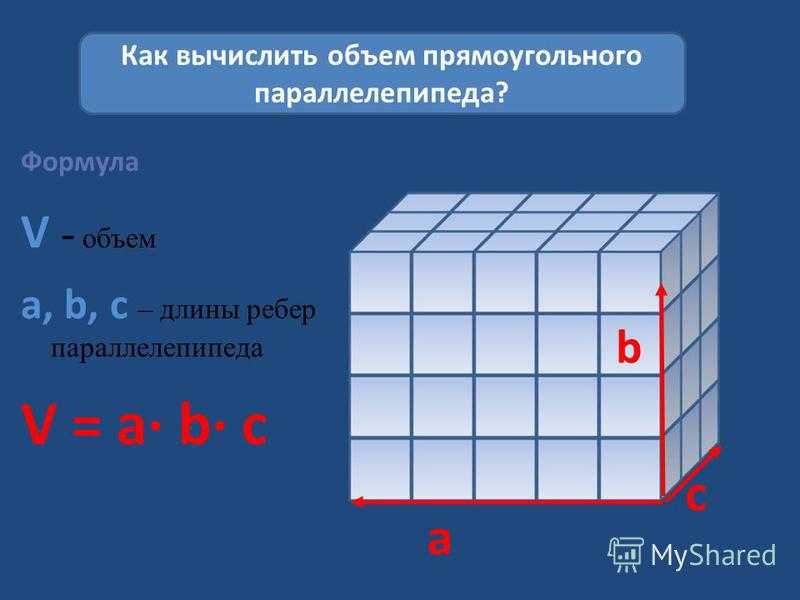
Выразим с через а и b: с=а-2*b
Математическая модель для решения нашей задачи построена.
Этап 3. Компьютерная реализация модели
Откройте табличный процессор и создайте таблицу. Сохраните таблицу под именем Объём. В ячейке А7 будем хранить длину стороны квадрата. Эта величина не меняется в процессе решения задачи.
В столбец В, начиная с ячейки В7, будем записывать высоту коробки. Начальное значение высоты – о см. Эта величина будет нарастать с заданным шагом. В столбце С, начиная с ячейки С7, будем вычислять длину основания коробки в зависимости от величины выреза по формуле с=а-2*b. Переведём эту формулу на язык табличного процессора, предварительно вспомнив: «Какая величина в процессе решения задачи не меняется?» Остаётся постоянной длина стороны листа, поэтому формула имеет вид: =А$7-2*В7.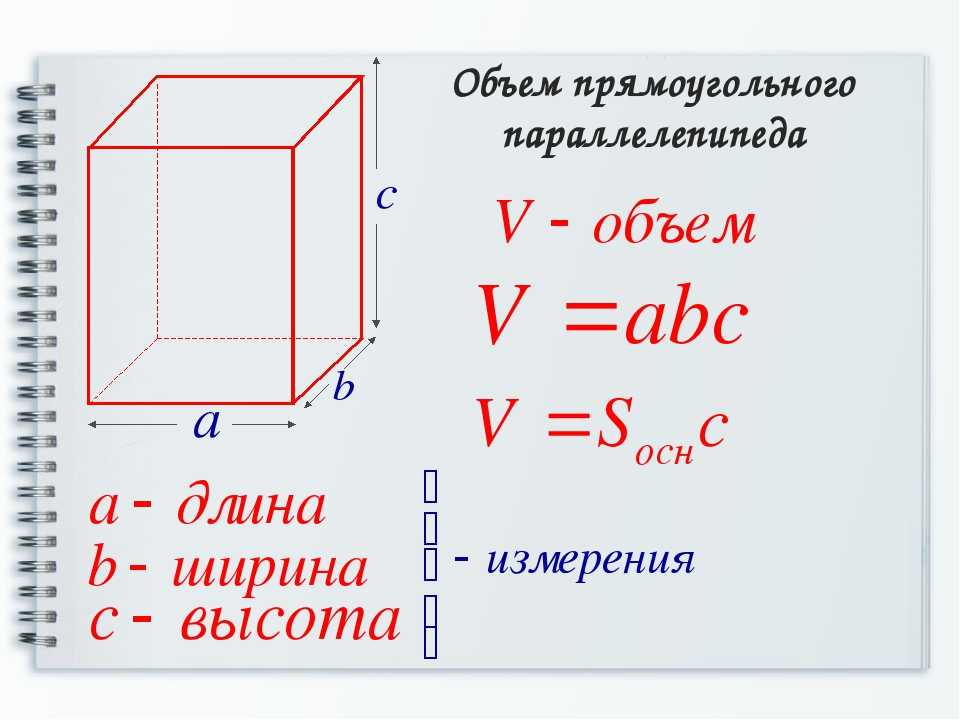
Этап 4. Компьютерный эксперимент
Приступим к самой интересной части нашей работы. Пусть длина стороны квадратного листа равна 1м или 100 см. Будем постепенно увеличивать высоту коробки (величину выреза) для того, чтобы найти наибольший объём. Высоту коробки будем менять, задавая шаг. Подготовьте таблицу для записи результатов эксперимента. В графу «Величина выреза» запишите простым карандашом предполагаемые ответы – высоту коробки. После окончания эксперимента, у нас появится возможность сравнить Ваш прогноз и результаты расчетов. В ячейку В7 запишем начальное значение величины выреза – 0 см. В ячейку В8 запишем величину шага – 1 см.
Проанализируем полученные результаты. Очевидно, что ответ находится в строке номер 24. При величине выреза 17 см наибольший объём равен 74052 куб.см.
Для более наглядного представления, выделим данные в диапазоне ячеек D7:D57 и построим график (гистограмму) зависимости объёма коробки от величины выреза. Продолжим эксперимент. Изменим величину шага. В ячейку В8 внесём 2 см. Выделите ячейки В7 и В8 и выполните автоматическое заполнение следующих за ними ячеек. Какой теперь вы получили результат? Сравните новый результат с предыдущим.
Проведём заключительный опыт. Уменьшим величину шага. В ячейку В8 запишем число 0,5. Занесите результат в таблицу ответов: При величине выреза 16,5 см наибольший объём равен 74068,5 куб.см.
Уменьшим величину шага. В ячейку В8 запишем число 0,5. Занесите результат в таблицу ответов: При величине выреза 16,5 см наибольший объём равен 74068,5 куб.см.
Этап 5. Анализ результатов
Проанализируйте полученные результаты и в рабочей тетради сделайте краткие выводы.
Ответьте на вопросы.
- Возможно ли проведение большего количества опытов?
- Является ли наш «наилучший» результат окончательным?
- Можно ли признать полученный нами результат удовлетворительным и почему?
- Сравните результаты компьютерного моделирования с предполагаемыми ответами.
IV. Физкультминутка
V. Обсуждение пройденного материала и подведение итогов урока. Результатом решения задачи является вывод о том, что по итогам проведенных опытов наибольший объём коробки равен 74068,5 куб.см. при величине выреза 16,5 см.
VI. Домашнее задание. Учащимся выдаются карточки с домашним заданием.
ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
Использование презентации и средств мультимедиа
После объявления темы, целей и задач урока на этапе мотивации учебной деятельности и актуализации знаний учащихся предполагается обращение к презентации. Учитель демонстрирует этапы решения задачи, объясняет содержание экспериментов, указывает способ записи промежуточных результатов и вывода. Ученики включаются в обсуждение предстоящей работы, после чего приступают к выполнению задания.
В презентации представлено полное содержание практической работы. Это цели и задачи урока, повторение теоретического материала, формулировка решаемой задачи, рисунки, схемы, все этапы решения, содержание и результаты экспериментов, таблицы, графики, домашнее задание с подробным решением.
Поэтому, проводя урок, учитель может использовать всю презентацию или ее фрагменты, увеличивать или уменьшать число экспериментов, применять раздаточный материал: таблицы для занесения результатов опытов, карточки с домашним заданием.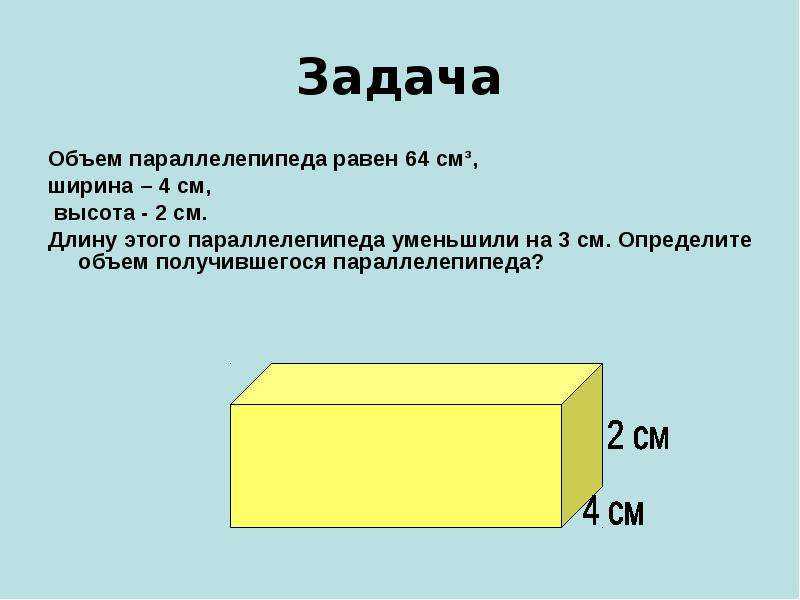
Сcылка для скачивания презентации: http://edu.letitbit.net
При изучении данной темы, целесообразно использовать средства мультимедиа, так как именно это позволяет ученику за малый промежуток времени охватить взглядом весь урок, понять смысл предстоящей работы и предполагаемый результат, то есть выстроить четкую картину действий. Этому особенно способствуют наглядные объекты – чертежи, схемы, графики, диаграммы, таблицы.
Все изложенное выше приводит к успешному решению поставленной задачи.
Вопросы для устной работы на этапе актуализации опорных знаний
- Моделирование – это замена одного объекта (процесса или явления) другим, при условии схранения всех существенных свойств исходного объекта (процесса или явления)
- Модель – это заменяющий объект (процесс или явление) Приведите примеры объектов, процессов и явлений и их моделей.
- Приведите примеры существенных и несущественных свойств одного и того же объекта, процесса или явления
- Виды моделей: наглядные и информационные
- Информационная модель – это модель, представляющая объект (процесс или явление) набором параметров и связей между ними
- Основным языком информационного моделирования является язык математики
- Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями
- Процесс описания факторов модели с помощью параметров называется формализацией
- Умение «хорошо поставить задачу», т.
 е. построить модель, учитывающую все существенные факторы, является искусством построения модели
е. построить модель, учитывающую все существенные факторы, является искусством построения модели - Модель называется адекватной, если при испытаниях она даёт удовлетворительные результаты
- Приведите пример такой ситуации, когда компьютерное моделирование является единственно возможным способом решения поставленной задачи[3]
Проверка и оценивание ЗУНов
Учитель оценивает наиболее полные и точные ответы учащихся во время устной работы, а также проверяет и оценивает результат решения задачи, оформленный в виде кратких выводов в тетради. А именно: результаты компьютерных экспериментов, их анализ, выводы о величине выреза – высоте коробке, при заданной длине стороны квадратного листа, такой, чтобы ее объем был наибольшим.
Карточки с домашним заданием
Постройте математические модели для приведенных ниже задач. Сравните полученные модели. Запишите выводы.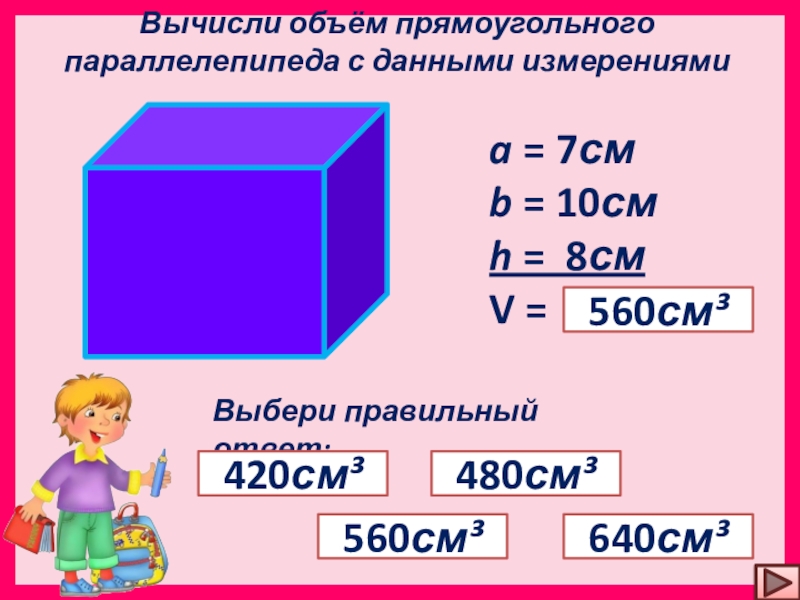
Задача 1. Первая труба наполняет бассейн за а минут, а вторая – за b минут. За какое время обе трубы наполнят бассейн, работая одновременно?[2]
Задача 2. Два теплохода одновременно отошли от разных пристаней и направились по озеру навстречу друг другу. Первый теплоход преодолевает все расстояние за c часов, а второй – за d часов. Через сколько часов теплоходы встретятся?[2]
Решите задачу с помощью электронных таблиц, используя приведенную ниже математическую модель.
Задача 3. Скорость распространения звука в воздухе в зависимости от температуры может быть найдена приближенно по формуле v=331+0,6t, где v – скорость (в метрах в секунду), t – температура (в градусах Цельсия). Найдите, с какой скоростью распространяется звук зимой при температуре воздуха от -35˚С до -20˚ С и летом при температуре воздуха от 20˚ С до 35˚.[2]
Логический переход от данного урока к последующим
Представленный урок является первой Практической работой из серии работ по теме «Компьютерное моделирование».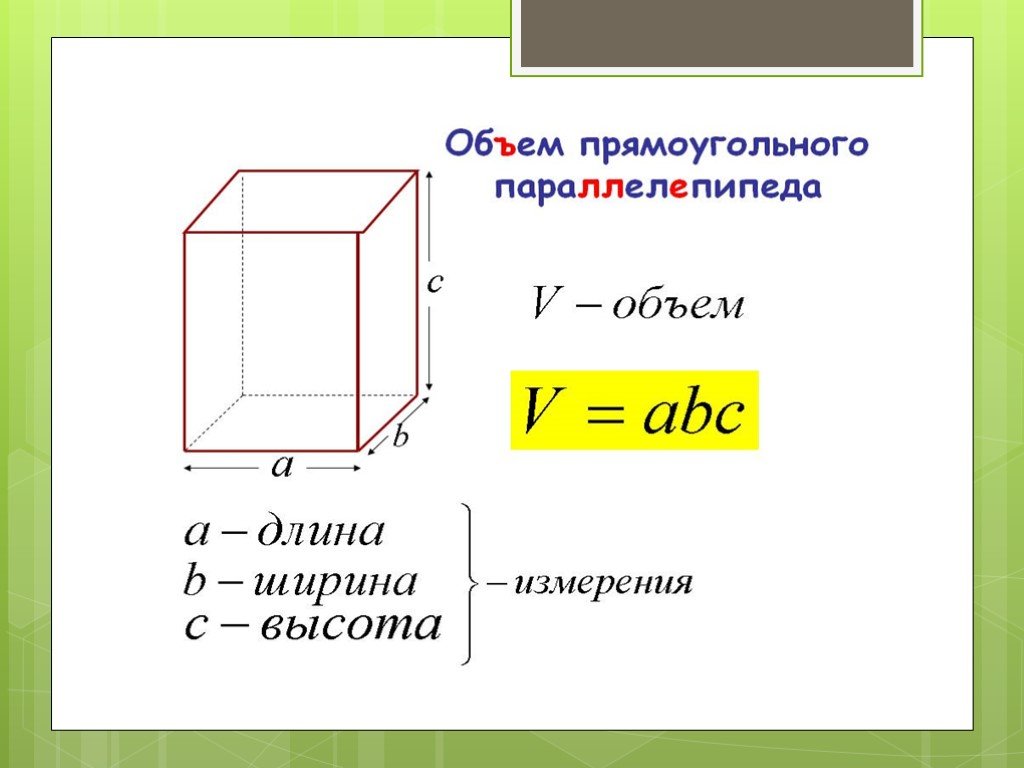 В процессе решения несложной задачи необходимо было рассмотреть все этапы построения и применения компьютерной модели.
В процессе решения несложной задачи необходимо было рассмотреть все этапы построения и применения компьютерной модели.
Далее мы переходим к решению задач «Прирост массы растений», отрабатывая «Модель неограниченного роста», «Модель ограниченного роста», «Модель потребления возобновляемых ресурсов»[3], адаптированные для учащихся 6 класса.
В результате завершения работ по всему циклу и опираясь на результаты компьютерного моделирования, дети с большим удовольствием отвечают на вопрос: «Сколько можно брать у живой природы, чтобы ее запасы не истощались?», что само по себе имеет большое воспитательное значение, акцентирует внимание детей на бережном отношении к окружающей среде и находит отклик в душах детей среднего школьного возраста.
Для оформления уроков выбраны картинки живой природы с целью придания единого смысла всем практическим работам, логическим завершением которых являются задачи о разумном подходе к потреблению природных ресурсов.
Список литературы
- Н. В. Макарова «Информатика 7–9 задачник по моделированию», Санкт-Петербург, Питер, 2001
- Л.Л. Босова, В. В. Трофимова, А. Ю. Босова «Изучаем информационные технологии в 7 классе: информационное моделирование», «Информатика в школе», Москва, Образование и информатика, 2007
- А. Г. Гейн, А.Н.Сенокосов, Н. А. Юнерман «Информатика 10–11», Москва, Просвещение, 2004
Правильный шестиугольник. Как рассчитать объем коробки
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Сторона коробки — a
Сторона коробки — b
Высота коробки — h
Кол-во коробок
Объем одной коробки
0
м 3
Объем всего груза
0
м 3
Расчет объема груза в м3
Рассчитать объем груза в м3 можно в нашем калькуляторе.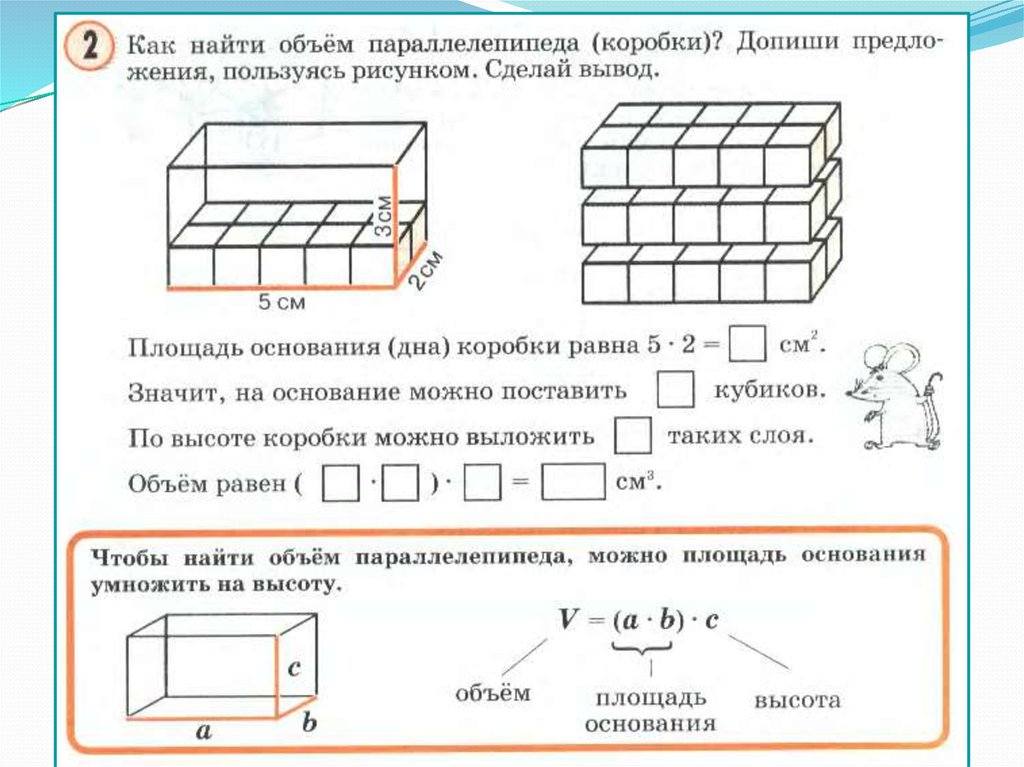 Зачем и кому это нужно? Например, Вы грузоотправитель, который хочет разобраться в ценах рынка грузоперевозок и для начала хочет быстро рассчитать объем своего груза в м3. Для расчета можно воспользоваться калькулятором. Указывая размеры сторон и высоту одной коробки, затем указывая кол-во коробок, в результате мы получаем их объем. Причем в данном калькуляторе можно увидеть как объем всего груза, так и только одной коробки. Выяснив объем своего груза, Вы без труда сможете понять, какой именно транспорт Вам необходим. Ведь, если объем Вашего груза составляет 10м3, то незачем заказывать фуру и переплачивать за «пустоту». Вам будет достаточно и газели.
Зачем и кому это нужно? Например, Вы грузоотправитель, который хочет разобраться в ценах рынка грузоперевозок и для начала хочет быстро рассчитать объем своего груза в м3. Для расчета можно воспользоваться калькулятором. Указывая размеры сторон и высоту одной коробки, затем указывая кол-во коробок, в результате мы получаем их объем. Причем в данном калькуляторе можно увидеть как объем всего груза, так и только одной коробки. Выяснив объем своего груза, Вы без труда сможете понять, какой именно транспорт Вам необходим. Ведь, если объем Вашего груза составляет 10м3, то незачем заказывать фуру и переплачивать за «пустоту». Вам будет достаточно и газели.
Как посчитать объем коробки в метрах кубических
Объем коробки посчитать очень просто. На этой странице расположен калькулятор, который поможет Вам легко посчитать объем одной коробки или всего груза. Возможно, Вам интересно по какой формуле идет расчет. С точки зрения математики обычная картонная коробка с грузом — это прямоугольный параллелепипед, а если у коробки все стороны равны, то это куб. Соответственно их объем будем рассчитывать по простой геометрической формуле: сторона А * сторона Б * высота. Стоит отметить важный факт: если при расчетах используется величина, например, метр, то и результат будет в кубических метрах. В нашем калькуляторе используются метры для расчета объема. Если одна из сторон коробки, к примеру, 60см, то в калькуляторе нужно указать десятичную дробь в виде: 0.6.
Соответственно их объем будем рассчитывать по простой геометрической формуле: сторона А * сторона Б * высота. Стоит отметить важный факт: если при расчетах используется величина, например, метр, то и результат будет в кубических метрах. В нашем калькуляторе используются метры для расчета объема. Если одна из сторон коробки, к примеру, 60см, то в калькуляторе нужно указать десятичную дробь в виде: 0.6.
Калькулятор объема коробки с грузом в м3
Мы уже выяснили, каким образом рассчитывается объем в м3. Для того, чтобы не считать данную величину вручную и был создан данный калькулятор объема. Зачем пользоваться эти калькулятором? Это удобно, не нужно тратить время на расчет объема всего груза в кубических метрах (м3). Используя простой интерфейс нашего калькулятора можно моментально узнать объем груза. Просто вписываем размеры сторон коробки, высоту коробки (третью сторону) и кол-во коробок, если их больше, чем одна. И все, получаем результат в виде значения в формате м3 (метры кубические).
Почему лучше использовать наш калькулятор вместо расчетов вручную? Вероятность ошибки в данном случае исключена, да и Вам намного меньше нужно тратить времени и сил на подсчеты вручную.
Для чего знать объем перевозимого груза?
Если Вы собираетесь заказать грузоперевозку чего-либо, упакованного в коробки или прямоугольные контейнеры, то первое, что спросят Вас при оформлении заявки это объем перевозимого груза. Вот тут Вам поможет наш калькулятор объема в м3. Прямо во время звонка Вы можете быстро рассчитать объем в м3 и сообщить его для оформления заявки.
Зная объем, менеджер-логист сможет подобрать необходимый автомобиль для перевозки именно Вашего груза и избавит Вас от ненужных переплат за автомобиль бОльшего размера. Также логист сразу сможет сориентировать Вас по цене грузоперевозки.
Количество коробок
Результат:
Объем одной коробки(м 3):
Общий объем(м 3):
Используйте полученный
результат для
оформления заявки
| d= | м см | |
| h= | м см |
Количество труб
Результат:
Объем одной трубы(м 3):
Общий объем(м 3):
Используйте полученный
результат для
оформления заявки
У вас возник вопрос о доставке , а так же возникла необходимость знать, как вычислить объем груза, нужна наша помощь? Как вычислить объем груза мы знаем, на этой странице вы видите калькулятор, который точно выполнит расчеты.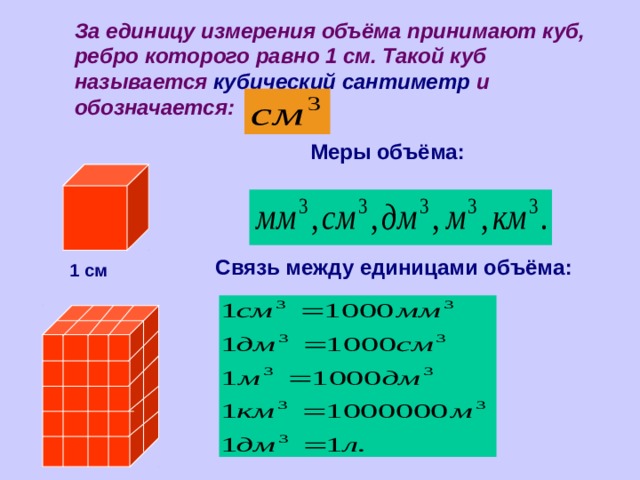
А вообще, для какой цели рассчитывается объем?
Объем рассчитать необходимо для того, чтобы избежать недоразумений при погрузке груженых коробок в транспортное средство. Объем рассчитать при помощи современных технологий сегодня несложно, достаточно вашего нахождения тут.
Какие критерии мы используем для подсчета объема груза?Во-первых , все знают — в процессе доставки важна каждая деталь, и немаловажно без ошибок посчитать объем груза в целом. Посчитать объем груза как уже говорилось поможет наш калькулятор объемов, он сделает это быстро и надежно!
Второе — калькулятор объемов, о его начини на нашем сайте, уже сказано выше, как видите, мы заботимся о наших клиентах. Калькулятор объемов, вот что может максимально облегчить работу с расчетами, и напрочь убить ваши сомнения.
Что мы вам даём?
Что же еще необходимо?
Например…
Вы предприниматель, который занимается перевозками из Китая, и Вам постоянно необходим калькулятор расчета объема. Калькулятор расчета объемов вы быстро найдёте на страницах нашего сайта, и выполните свои расчеты сейчас же.
Калькулятор расчета объемов вы быстро найдёте на страницах нашего сайта, и выполните свои расчеты сейчас же.
В наше время предпринимательство держится на Китайском производстве товаров, а от куда возникла потребность рассчитать объем? Рассчитать объем необходимо для того что бы узнать общий объём груза, и далее выбрать вид транспорта.
Чем же является расчет объемов в доставке? И какую роль он играет?
Расчёт объема — это насколько, вы уже поняли очень важный этап в доставке, и доверять его надо в надёжные руки профессионалов. Расчёт объема груза надо делать тщательно, учитывая все размеры, и переведя их в метры кубические.
Но к сожалению, не все справляются с этими расчетами.
Еще в школьные времена мы изучали то как посчитать объем груза в м3, но к сожалению, всего этого не запомнишь. Как посчитать объем груза в м3 — бывают случаи когда этот вопрос встаёт на первое место, например во время доставки.
Для этого данная страница и существует!
Ведь эта страница для того и предназначена, чтобы помогать Вам в расчёте доставки.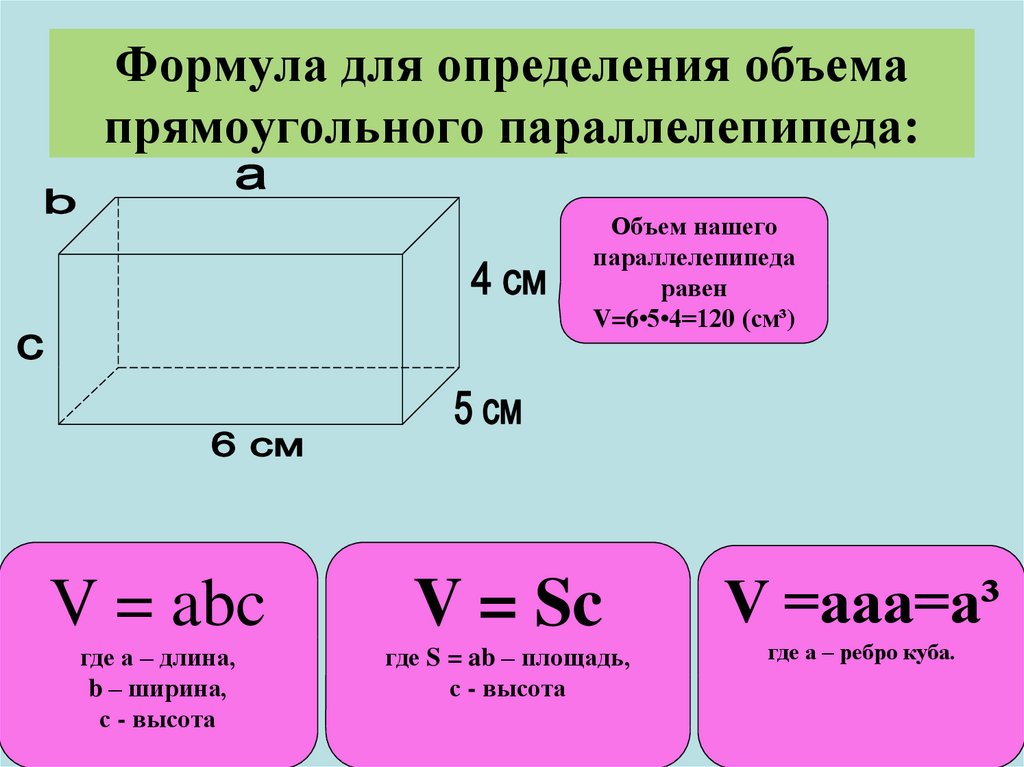
Что бы выполнить расчет объема коробки, не надо стараться это делать самостоятельно, просто надо заполнить пустые поля. Расчет объема коробки автоматически выполнится нашим калькулятором, если вы сомневаетесь, проверьте сами.
Для этого мы и напомнили Вам формулу объемов.
Расчет объема груза в кубометрах необходим Вам для того, чтобы подать правильную заявку для его перевозки. Расчет объема груза в кубометрах, т. е. знание самого объема поможет определиться с тем какой вид доставки Вам подойдет.
А теперь перейдем к основному , поговорим о том, как совершать расчеты и для чего они необходимы.
Для начала разберемся…
Рассчитать объем груза не всегда просто, как кажется, всё это из-за того что, коробки могут быть разнообразной формы. Рассчитать объем груза прямоугольной коробки, пустяк, а вот остальных тяжеловато, необходимо знать формулы.
Для начала определим форму, для этого сначала узнаем, какие они существуют.
Какую форму может иметь коробка:
- Прямоугольника;
- Цилиндра;
- Усеченной пирамиды (очень редко).

Затем следуют измерения
Перед тем, как вычислить объем коробки измерим её, но запомните, чем точнее сделаны измерения, тем легче Вам. «Как вычислить объем коробки?» — что делать дальше: определить, какой она формы (куба или прямоугольника), размеры.
Что нам дает знание объёма?
Знание объёма коробки не позволит допустить недоразумений при погрузке товаров в любой вид транспорта, который может быть. От объёма коробки практически не чего не зависит, скорее наоборот все зависит от размеров самого товара.
А почему? Тут всё очевидно, прежде чем приобрести коробку, надо узнать размер груза, который Вы собираетесь перевозить через границу.
Ну вот Вы знаете размеры груза, теперь остаётся посчитать его объем (что бы приобрести коробу).
Итак , для того чтобы узнать, как рассчитать объем груза в м3 формула потребуется в первую же очередь. Как рассчитать объём груза в м3 формула поможет без сомнений в этом вопросе, вот так она выглядит V=a*b*h, всё очень просто.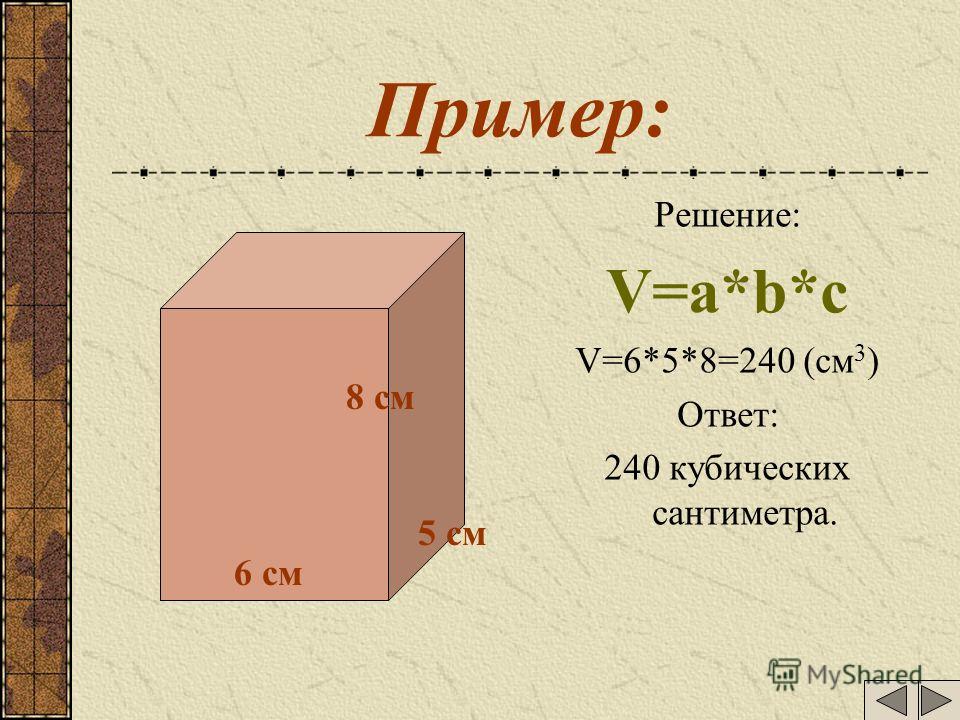
Тем более она уже вам известна.
Хотим напомнить о том что…
Что бы Вам стало легче определить, какой вид транспорта выбрать для доставки, надо рассчитать объем груза в м3. Рассчитать объем груза в м3 очень просто, тут необходимо знать точные размеры, которые затем необходимо перемножить.
Единицы необходимо пе6реводить именно в м3, иначе не получится посчитать доставку.
А что делать, если форма коробки не прямоугольная, а округлая? Ведь это большая редкость, но все же бывает.
Можно объем посчитать коробки или ёмкости в основании которых лежит круг, и для этого так же существует формула. Объем посчитать коробки формой круга позволяет выражение V *r2*h, размеры прежде всего надо безошибочно измерить.
Калькулятор объемов
Предоставляем к вашему вниманию калькулятор: объем грузов в м3, с помощью него вы можете самостоятельно делать расчёты. Калькулятор объем грузов расположен на наем сайте специально для вашего удобства, и для быстроты расчетов.
Для чего нужен калькулятор расчета объема груза?
Мы с вами деловые люди и потерянное время порой несёт в себе большие минусы. Хотите получать грузы быстро и надёжно? И при этом в максимально короткие сроки узнавать цены на их перевозку и доставку?
Вот именно здесь, поможет калькулятор объёма груза!
Наш калькулятор объёмов позволяет вам рассчитать объём груза в м3, поэтому вопрос о объёме коробки больше не возникнет. Калькулятор объёмов простой и удобный в применении, он выдаст результаты как объёма коробки так и груза.
Итак, с помощью калькулятора объёма Вы решаете несколько вопросов:
Как вычислить объем груза (или коробки)? Не забывайте о количественной единице, которую вы берёте в расчёт.
Столкнулись с одним из них или возник подобный? Наша компания рада предложить для Вашего удобства объем в метрах кубических коробки посчитать, с помощью удобного калькулятора.
А напоследок, давайте вспомним математику!
Какая проблема самая распространённая?
Многие путают то как вычислять объём плоских фигур и объемных, т. к., ошибаются в понятиях, точнее затрудняются с ответом. Как вычислять объём не надо знать, хватит того, что вы укажете размеры, главное не забывайте, что их 3.
к., ошибаются в понятиях, точнее затрудняются с ответом. Как вычислять объём не надо знать, хватит того, что вы укажете размеры, главное не забывайте, что их 3.
Закончив все расчеты, остается еще одна задача.
А какой Вам нужен транспорт?
Напомним, в доставке кроме того, как рассчитать кубатуру есть еще не менее важные вещи, например размещение товаров. Как рассчитать кубатуру вы знаете, поэтому всё остальное в ваших руках, теперь выбор транспорта зависит от вас.
Сторон. Р = а1+а2+а3+а4+а5+а6,где P – периметр шестиугольника , а а1, а2 … а6 – длины его сторон.Единицы измерения каждой из сторон приведите к одному виду – в этом случае достаточно будет сложить только числовые значения длин сторон. Единица измерения периметра шестиугольника будет совпадать с единицей измерения сторон.
Примеры из реальной жизни
Геометрия — это отрасль математики, которая занимается изучением форм различных измерений и анализом их свойств. В этом исследовании форм многоугольное семейство является одной из наиболее часто изучаемых фигур. Многоугольники закрыты 2-мерными плоскими объектами, которые имеют прямые стороны. Многоугольник, состоящий из 6 сторон и 6 углов, известен как шестиугольник. Любая замкнутая плоская двумерная структура с 6 прямыми сторонами будет называться шестиугольником. Слово «шестнадцатеричный» означает 6, а «угол» относится к углу.
Многоугольники закрыты 2-мерными плоскими объектами, которые имеют прямые стороны. Многоугольник, состоящий из 6 сторон и 6 углов, известен как шестиугольник. Любая замкнутая плоская двумерная структура с 6 прямыми сторонами будет называться шестиугольником. Слово «шестнадцатеричный» означает 6, а «угол» относится к углу.
Пример.Имеется шестиугольник с длинами сторон 1 см, 2 мм, 3 мм, 4 мм, 5 мм, 6 мм. Требуется найти его периметр.Решение.1. Единица измерения первой стороны (см) отличается от единиц измерения длин остальных сторон (мм). Поэтому, переведите: 1 см = 10 мм.2. 10+2+3+4+5+6=30 (мм).
Если шестиугольник правильный, то чтобы найти его периметр, умножьте длину его стороны на шесть:Р = а * 6,где а – длина стороны правильного шестиугольника .Пример.Найти периметр правильного шестиугольника с длиной стороны равной 10 см.Решение: 10 * 6 = 60 (см).
Как показано на диаграмме ниже, шестиугольник имеет 6 сторон или края, 6 углов и 6 вершин. Площадь шестиугольника — это пространство, занимаемое в границах шестиугольника. Используя измерения стороны и угла, мы можем найти область шестиугольника. Шестиугольники можно наблюдать в разных формах в нашей красивой природе. На приведенном ниже рисунке показана заштрихованная часть внутри границ шестиугольника, которая называется зоной шестиугольника.
Используя измерения стороны и угла, мы можем найти область шестиугольника. Шестиугольники можно наблюдать в разных формах в нашей красивой природе. На приведенном ниже рисунке показана заштрихованная часть внутри границ шестиугольника, которая называется зоной шестиугольника.
Этот тип шестиугольника также не имеет 6 равных углов. Если вершины нерегулярного шестиугольника направлены наружу, то он известен как выпуклый нерегулярный шестиугольник, а если вершины шестиугольника направлены внутрь, то он известен как вогнутый нерегулярный шестиугольник, как показано на рисунке ниже. Поскольку измерения сторон и углов неравны, поэтому мы должны использовать разные стратегии, чтобы найти область нерегулярного шестиугольника. Метод вычисления площади правильного шестиугольника отличается от метода расчета площади нерегулярного шестиугольника.
Правильный шестиугольник обладает уникальным свойством: радиус описанной вокруг такого шестиугольника окружности равен длине его стороны. Поэтому, если известен радиус описанной окружности, до воспользуйтесь формулой:P = R * 6,где R – радиус описанной окружности.
Поэтому, если известен радиус описанной окружности, до воспользуйтесь формулой:P = R * 6,где R – радиус описанной окружности.
Область регулярного шестиугольника: правильный шестиугольник имеет все 6 сторон и 6 углов, равных по мере. Когда тянутся диагонали, проходящие через центр шестиугольника, образуются 6 равносторонних треугольников одинакового размера. Если рассчитывается площадь одного равностороннего треугольника, то мы можем легко вычислить площадь данного правильного шестиугольника. Следовательно, все его стороны также равны.
Теперь правильный шестиугольник состоит из 6 таких конгруэнтных равносторонних треугольников. Пример 1: Какова площадь правильного шестиугольника, длина которого составляет 8 см? Пример 2: Если площадь правильного шестиугольника составляет √12 квадратных футов, то какова длина стороны шестиугольника?
Пример.Рассчитать периметр правильного шестиугольника , писанного в окружность диаметром 20 см.Решение. Радиус описанной окружности будет равен: 20/2=10 (см). Следовательно, периметр шестиугольника : 10 * 6 = 60 (см).
Следовательно, периметр шестиугольника : 10 * 6 = 60 (см).
Пример: найдите область нерегулярного шестиугольника, показанного на рисунке ниже. Шестиугольные сетки используются в некоторых играх, но они не так просты или распространены как квадратные сетки. Многие части этой страницы являются интерактивными; выбор типа сетки будет обновлять диаграммы, код и текст для соответствия. Образцы кода на этой странице написаны в псевдокоде; они предназначены для легкого чтения и понимания, чтобы вы могли написать свою собственную реализацию.
Шестиугольники — это шестигранные многоугольники. Обычные шестиугольники имеют все стороны одинаковой длины. Типичные ориентации для гексарифмических сеток являются горизонтальными и вертикальными. Каждое ребро разделяется двумя шестиугольниками. Каждый угол разделяется тремя шестиугольниками. В моей статье о частях сетки. В правильном шестиугольнике внутренние углы 120 °. Есть шесть «клиньев», каждый из которых равносторонний треугольник с углами 60 ° внутри.
Если по условиям задачи задан радиус вписанной окружности, то примените формулу:P = 4 * √3 * r,где r – радиус вписанной в правильный шестиугольник окружности.
Если известна площадь правильного шестиугольника , то для расчета периметра используйте следующее соотношение:S = 3/2 * √3 * а²,где S – площадь правильного шестиугольника . Отсюда можно найти а = √(2/3 * S / √3), следовательно:Р = 6 * а = 6 * √(2/3 * S / √3) = √(24 * S / √3) = √(8 * √3 * S) = 2√(2S√3).
Учитывая гексагон, который 6 гексов соседствуют с ним? Как и следовало ожидать, ответ прост с координатами куба, все еще довольно простой с осевыми координатами и немного сложнее с координатами смещения. Мы могли бы также захотеть рассчитать 6 диагональных гексов.
Учитывая местоположение и расстояние, что видно из этого места, а не заблокировано препятствиями? Самый простой способ сделать это — нарисовать линию для каждого гексагонального диапазона. Если линия не ударяет по стенам, вы можете увидеть гекс. Мышь над шестнадцатеричным, чтобы увидеть, как линия тянется к этому гексу, и к каким стенам он попадает.
Мышь над шестнадцатеричным, чтобы увидеть, как линия тянется к этому гексу, и к каким стенам он попадает.
По определению из планиметрии правильным многоугольником называется выпуклый многоугольник, у которого стороны равны между собой и углы так же равны между собой. Правильный шестиугольник является правильным многоугольником, с числом сторон равным шести. Существует несколько формул для расчета площади правильного многоугольника.
- Выпуклый семиугольник — это тот, у которого нет тупых внутренних углов.
- Вогнутая спираль — одна с тупым внутренним углом.
Формулы для расчета площади и периметра семиугольника варьируются в зависимости от того, является ли он регулярным или нерегулярным семиугольником.
где а – длина стороны правильного шестиугольника.
Пример.
Найти периметр правильного шестиугольника с длиной стороны равной 10 см.
Решение: 10 * 6 = 60 (см).
Правильный шестиугольник обладает уникальным свойством: радиус описанной вокруг такого шестиугольника окружности равен длине его стороны. Поэтому, если известен радиус описанной окружности, до воспользуйтесь формулой:
Поэтому, если известен радиус описанной окружности, до воспользуйтесь формулой:
где R – радиус описанной окружности.
Пример.
Рассчитать периметр правильного шестиугольника, писанного в окружность диаметром 20 см.
Решение.
Радиус описанной окружности будет равен: 20/2=10 (см).
Следовательно, периметр шестиугольника: 10 * 6 = 60 (см).
Если по условиям задачи задан радиус вписанной окружности, то примените формулу:
где r – радиус вписанной в правильный шестиугольник окружности.
Если известна площадь правильного шестиугольника, то для расчета периметра используйте следующее соотношение:
S = 3/2 * v3 * а?,
где S – площадь правильного шестиугольника.
Отсюда можно найти а = v(2/3 * S / v3), следовательно:
Р = 6 * а = 6 * v(2/3 * S / v3) = v(24 * S / v3) = v(8 * v3 * S) = 2v(2Sv3).
Как просто
Объем квадратного ящика
LearnPracticeDownload
Объем квадратного ящика — это пространство, занимаемое квадратным ящиком или кубом. Квадратный ящик — это трехмерный твердотельный объект, имеющий форму куба, а куб — трехмерный твердотельный объект с шестью квадратными гранями. Куб также известен как правильный шестигранник и является одним из пяти платоновых тел. В этом разделе мы узнаем об объеме квадратного ящика вместе с несколькими решенными примерами и практическими вопросами.
Квадратный ящик — это трехмерный твердотельный объект, имеющий форму куба, а куб — трехмерный твердотельный объект с шестью квадратными гранями. Куб также известен как правильный шестигранник и является одним из пяти платоновых тел. В этом разделе мы узнаем об объеме квадратного ящика вместе с несколькими решенными примерами и практическими вопросами.
| 1. | Каков объем квадратной коробки? |
| 2. | Объем квадратной коробки Формула |
| 3. | Расчет объема квадратной коробки |
| 4. | Часто задаваемые вопросы об объеме квадратной коробки |
Каков объем квадратной коробки?
Объем квадратного ящика (V) можно определить как пространство, занимаемое квадратным ящиком или кубом. Мы можем найти объем квадратного ящика, просто зная длину его стороны. Объем квадратного ящика равен кубу длины стороны квадратного ящика.
Формула объема: V = s 3 , где «s» — длина стороны квадратного прямоугольника.
Объем квадратной коробки Формула
Объем квадратной коробки равен кубу длины стороны коробки. Формула объема квадратного ящика: V = s 3 , где s — длина стороны ящика. Мы также можем вычислить объем квадратной коробки или куба, если знаем длину диагонали коробки.
Формула объема квадратной коробки или куба с диагональю ‘d’ равна V = (√3 × d 3 )/9
Расчет объема квадратной коробки
Объем квадратной коробки равен V = s 3 . Следуя шагам, указанным ниже, мы можем найти объем квадратного ящика.
- Шаг 1 : Рассчитайте длину любой стороны коробки.
- Шаг 2 : Найдите куб длины стороны. Или используйте формулу V = (√3 × d 3 )/9, когда известна длина диагонали ‘d’.
- Шаг 3 : Представьте ответ в кубических единицах длины.

Важные замечания по объему квадратного ящика
- Объем квадратного ящика, если дана его сторона s, V = s 3
- Объем квадратного ящика, если дана длина его диагонали d, V = (√3 × d 3 )/9
- Объем квадратного ящика при заданных площади основания и высоте, V = площадь основания × высота
Темы, связанные с объемом квадратной коробки
- Объем призмы
- Объем прямоугольной призмы
- Калькулятор объема куба
Решенные примеры для объема квадратного ящика
Пример 1: Длина стороны квадратного ящика равна 5 дюймов. Найдите объем квадратного ящика.
Решение:
Длина стороны, s = 5 в
Используя формулу для объема квадратного ящика: V = s 3
⇒ V = 5 3
⇒ V = 125Ответ: Объем квадратной коробки 125 кубических дюймов.

Пример 2: Длина диагонали квадратного прямоугольника составляет √3 единицы. Найдите объем ящика.
Решение:
Длина диагонали = √3 единиц
Используя формулу для объема квадратной коробки: V = (√3 × d 3 )/9
⇒ V = [√3 × √(3 3 )]/9 = 1Ответ: Объем ящика равен 1 куб.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по объему квадратной коробки
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об объеме квадратной коробки
Что означает объем квадратной коробки?
Объем квадратного ящика относится к общему пространству, занимаемому квадратным ящиком в трехмерной плоскости.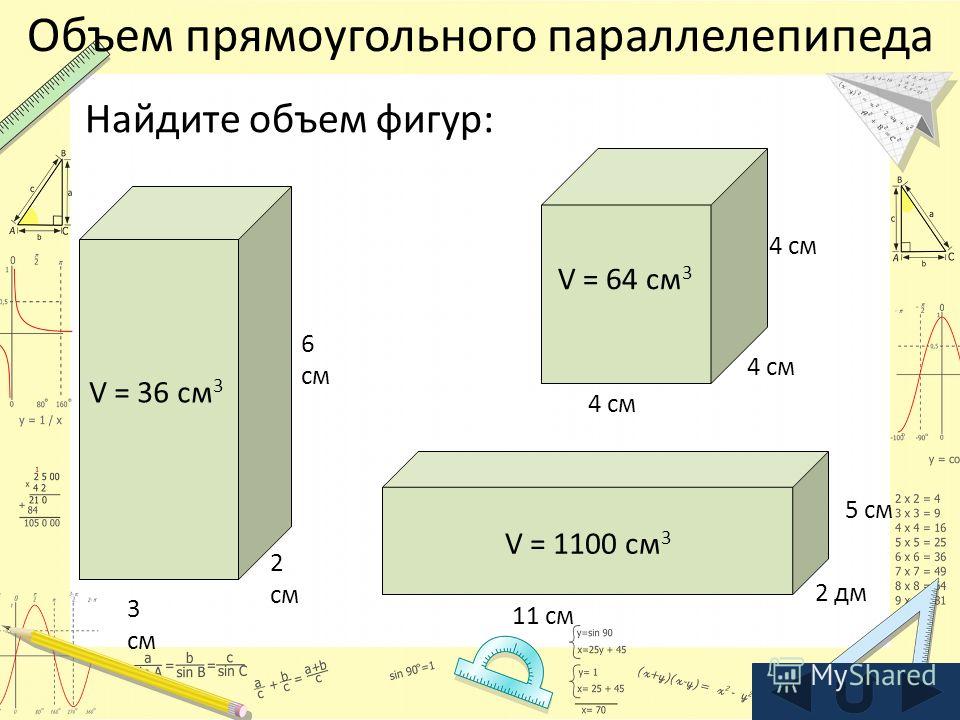 Выражается в кубических единицах.
Выражается в кубических единицах.
Как найти объем квадратной коробки тремя способами?
Три способа найти объем квадратного ящика следующие:
- Метод 1: Используя формулу объема с заданной длиной ребра: V = s 3
- Метод 2: Используя формулу объема, где дана длина диагонали: V = (√3×d 3 )/9
- Метод 3: Умножение площади основания на высоту объекта: V = площадь основания × h
Какова формула объема квадратной коробки?
Объем квадратной коробки можно рассчитать, используя длину стороны коробки. Объем квадратной коробки равен s 3 , где s — длина коробки.
Объем квадратной коробки измеряется в квадратных единицах?
Нет, объем квадратного ящика не измеряется в квадратных единицах, а рассчитывается в кубических единицах с использованием таких единиц, как см 3 , 3 , м 3 , фут 3 и т. д.
д.
Что такое квадратная коробка?
Трехмерный объект с шестью квадратными гранями называется квадратным блоком или кубом.
Сколько вершин в квадратной рамке?
В квадрате 8 вершин. Квадрат — это куб с 8 вершинами, 6 гранями и 12 ребрами.
Сколько граней у квадратной коробки?
Квадрат имеет 6 граней, поэтому он также известен как шестигранник и является одним из платоновых тел.
Скачать БЕСПЛАТНЫЕ учебные материалы
Volume Worksheet
Рабочие листы по математике и
наглядный учебный план
Объем куба: формула и примеры
Давайте научимся определять объем куба .
Что такое куб? Единственный правильный шестигранник, куб представляет собой трехмерный объект с шестью квадратными поверхностями или сторонами одинакового размера, 12 ребрами и 8 вершинами. Учитывая, что его квадратные стороны равны, отсюда следует, что длина, ширина и высота куба также равны. Примерами объектов в форме куба являются игральные кости, шкатулки для драгоценностей, кубики льда, кубики сахара и кубики Рубика.
Примерами объектов в форме куба являются игральные кости, шкатулки для драгоценностей, кубики льда, кубики сахара и кубики Рубика.
Вот иллюстрация куба. Обратите внимание, как в развернутом виде он образует 6 равных квадратных поверхностей или сторон. Получающаяся двумерная форма, когда куб разворачивается, называется сетью куба .
Как найти объем куба :Объем куба не только говорит о количестве занимаемого им пространства, но также измеряет его емкость или объем пространства внутри объекта, который может быть заполнен . Когда у вас есть полый кубический контейнер, который вы хотите наполнить водой, объем кубического контейнера необходим для определения его вместимости, то есть того, сколько воды он может вместить.
Примечание: Объем измеряется в кубических единицах, таких как см 3 , м 3 , км 3 и 3 . Что касается емкости куба, объем может быть измерен в литрах (л) или миллилитрах (мл).
Чтобы найти объем куба, умножьте его длину на ширину и высоту ( a • a • a ). Учитывая, что все длины квадратных сторон куба одинаковы, его формула объема записывается как:
V = a 3
где a = длина одной стороны куба
Шаг 1. Запишите данные числа. Вам понадобится длина стороны куба, чтобы найти объем. Убедитесь, что все единицы измерения одинаковы. Если нет, преобразуйте любой из них, чтобы он соответствовал другому.
Шаг 2. Подставьте цифры в формулу.
Шаг 3. Выполните операции. Не забудьте указать кубическую единицу объема.
Пример #1: Найдите объем куба, зная длину одной стороныНайдите объем куба ниже.
Решение для примера №1:
Шаг 1. Запишите данное измерение, a = 8м .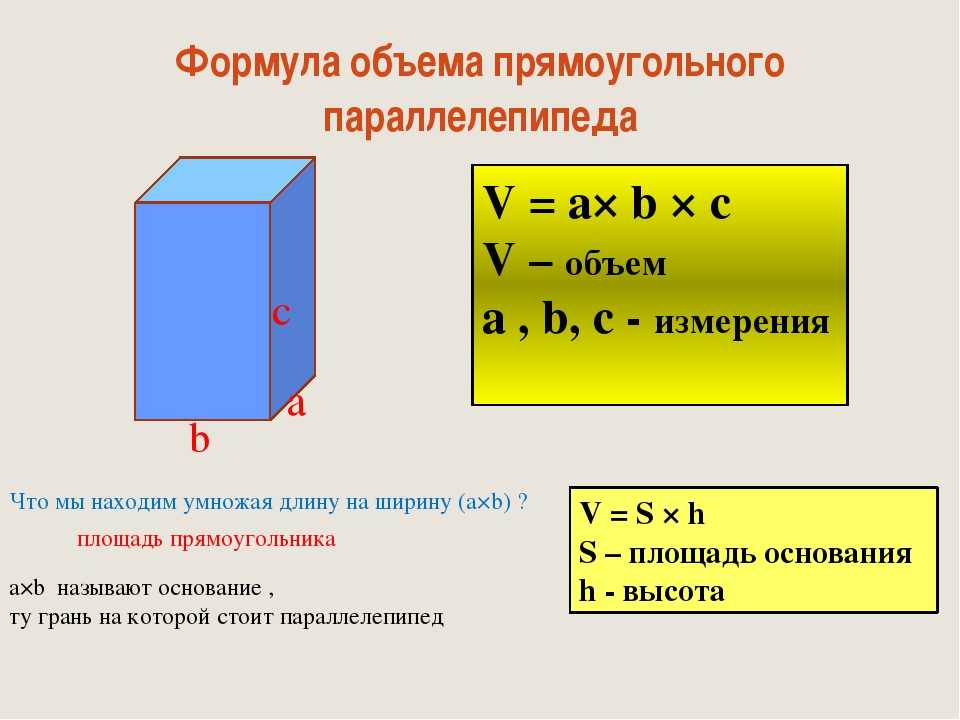
Шаг 2 . Подставьте 8m в формулу объема куба .
V = a 3
V = (8 см) 3
Шаг 3. Упростите и решите уравнение.
V = 512см 3
Следовательно, объем куба равен 512см 3 .
Хотите узнать, как найти площадь поверхности этого куба?
Связанное чтение: Площадь поверхности куба – формула и примеры
Пример 2. Найдите объем куба, зная длину одной стороны
Найдите объем куба , длина которого 3 см.
Решение для примера № 2:
Шаг 1. Запишите данные измерения, a = 3 см .
Шаг 2 . Подставьте 3 см в формулу объема куба .
В = a 3
В = (3 см) 3
Шаг 3.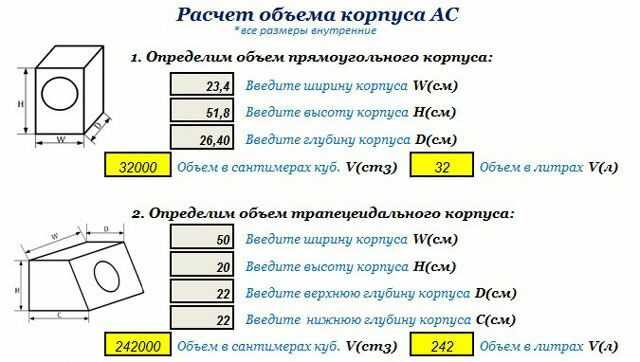 Упростите и решите уравнение.
Упростите и решите уравнение.
В = 27 см 3
Следовательно, объем куб 27см 3 .
Пример #3: Определение длины и площади поверхности при заданном объеме
Найдите длину и площадь поверхности приведенного ниже куба.
Решение для примера №3:
Начните с нахождения длины куба ( a ).
Шаг 1. Запишите данное измерение, В = 64 дюйма 3 .
Шаг 2. Определите длина куба ( a ) путем нахождения кубического корня из его объема, полученного по формуле: обе части уравнения объема, В = a 3 .
Шаг 3. Подставьте 64 в 3 вместо V в формуле, затем упростите и решите уравнение.
а = 3 √ (64 дюйма 3 )
a = 4 дюйма
Следовательно, длина куба равна 4 дюйма .
Теперь мы можем найти площадь поверхности куба, используя найденную длину.
Шаг 1. Замените 4 в на a в формуле площади поверхности куба.
SA = 6 a ²
SA = 6(4 дюйма)²
Шаг 2. Упростите и решите уравнение.
SA = 6(4 дюйма)²
SA = 96 дюймов²
Следовательно, площадь поверхности куба равна 96 дюймов² .
Пример №4. Определение вместимости контейнера
Сколько кубических коробок размером 2 см х 2 см х 2 см можно поместить в кубический контейнер со стороной 6 см?
Решение для примера № 4:
Чтобы найти количество коробок, которые могут поместиться в контейнере, разделите объем контейнера на объем коробок.
Шаг 1. Запишите данные: длина кубических ящиков ( a = 2см) , длина кубического контейнера ( a = 6см) .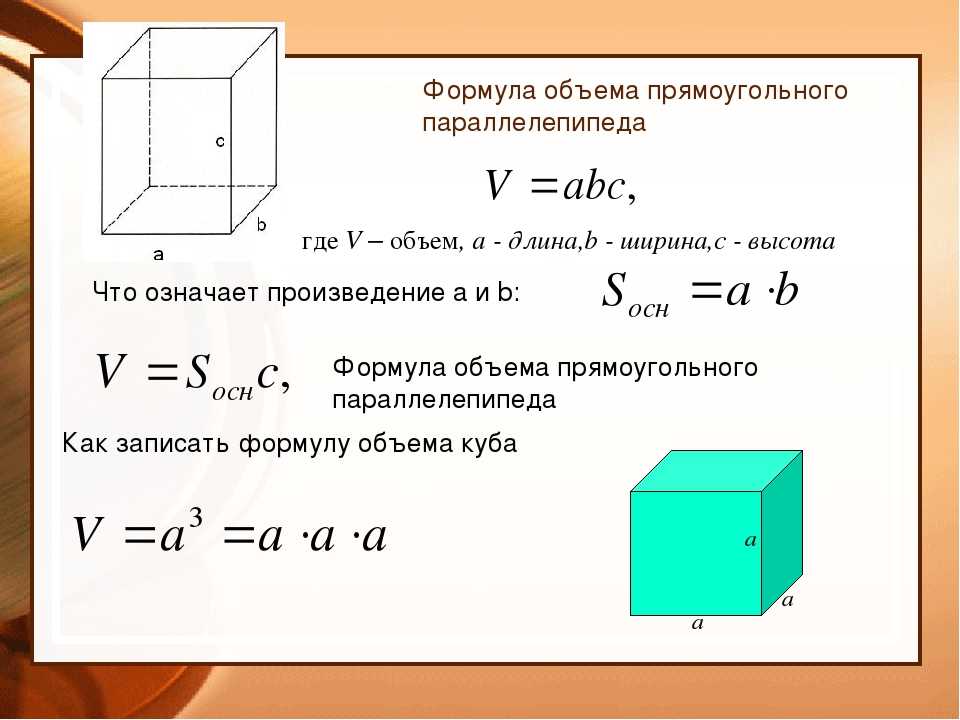
Шаг 2. Сначала вычислите объем кубических ящиков.
Замените 2 см на на в формуле объема.
V = a 3
V = (2 см) 3
Упростите и решите уравнение.
V = 8см 3
Следовательно, объем каждого кубического ящика равен 8см 3 .
Шаг 3. Вычислите объем кубического контейнера.
Замените 6 см на на в формуле объема.
V = a 3
V = (6 см) 3
Упростите и решите уравнение.
V = 216 см 3
Следовательно, объем кубического контейнера составляет 216см 3 .
Шаг 4. Разделите объем кубического контейнера на объем каждого кубического ящика, чтобы найти количество ящиков, которые поместятся в контейнер.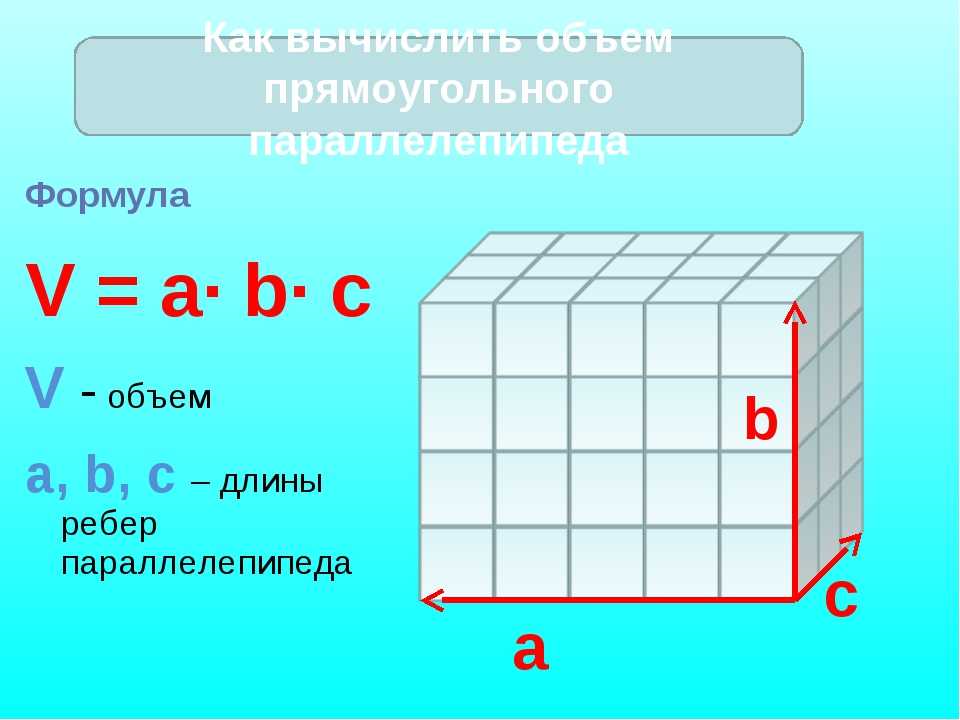

 е. построить модель, учитывающую все существенные факторы, является искусством построения модели
е. построить модель, учитывающую все существенные факторы, является искусством построения модели

