Как обозначаются пересекающиеся прямые: Пересекающиеся прямые. Точка пересечения | Перпендикуляр и наклонная

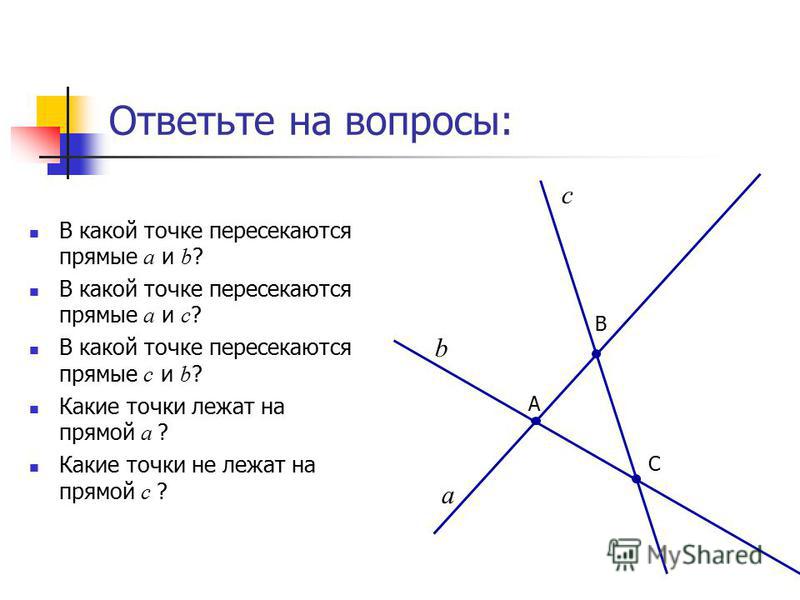
Обозначение пересекающихся прямых. Прямая в математике. Прямая на плоскости

Несмотря на то что геометрия относится к числу точных наук, ученые не могут однозначно дать определение термину «прямая». В самом общем виде можно дать такое определение: «Прямая — это линия, путь вдоль которой равен расстоянию между двумя точками».

Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности.

К основным понятиям геометрии относятся точка, прямая и плоскость, они даются без определения, но определения других геометрических фигур даются через эти понятия. Плоскость, как и прямая, — это первичное понятие, не имеющее определения. Это утверждение устанавливается следующей аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости. А само утверждение, которое доказывается, называется теоремой. Формулировка теоремы обычно состоит из двух частей.

Задача: где прямая, луч, отрезок, кривая? Вершины ломаной(похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.

Задача: какая ломанная длиннее, а у какой больше вершин? Смежные стороны многоугольника — это смежные звенья ломанной. Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.

На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка.

В дальнейшем будут определения для разных фигур кроме двух — точка и прямая. Значит иногда обозначить прямую можем и двумя большими латинскими буквами, например, прямая\(AB\), так как никакая другая прямая через эти две точки не может быть проведена. Символически записываем отрезок \(AB\).

Что такое точка в математике?

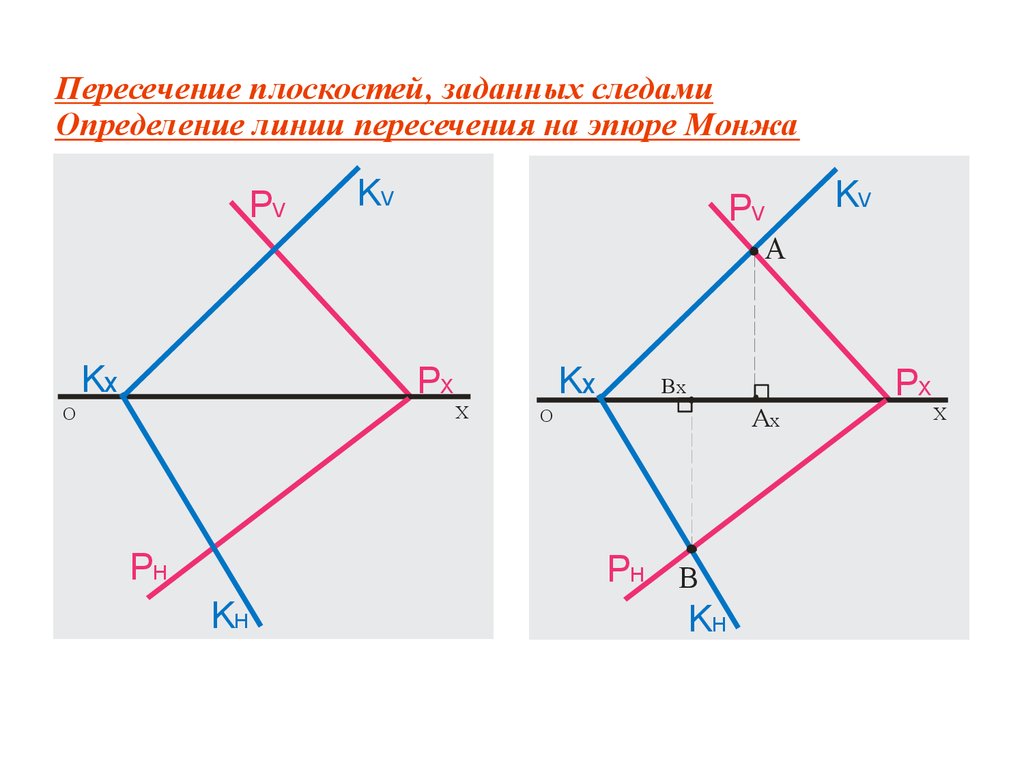
Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.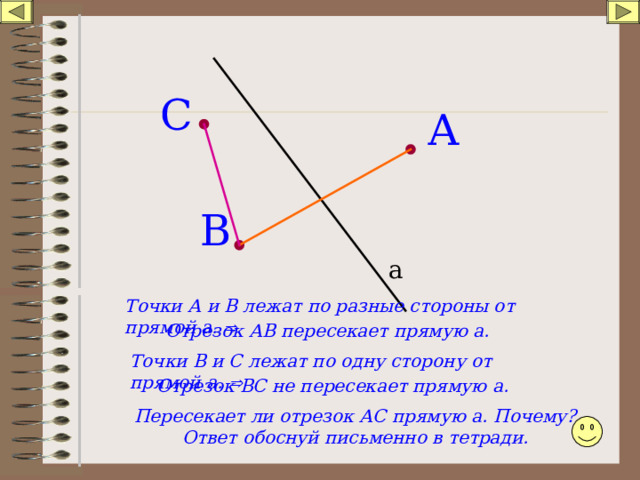

С. Вписанный угол, опирающийся на полуокружность, — прямой. Здесь собраны основные определения, теоремы, свойства фигур на плоскости.

Вектор с координатами точки называется нормальным вектором, он перпендикулярен прямой.

При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенно определяется аксиомами геометрии.

4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны. Лучом называют часть прямой линии, ограниченную с одной стороны. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.

Страница 1 из 3

§1. Контрольные вопросы
Вопрос 1. Приведите примеры геометрических фигур.
Ответ. Примеры геометрических фигур: треугольник, квадрат, окружность.

Вопрос 2. Назовите основные геометрические фигуры на плоскости.
Ответ. Основными геометрическими фигурами на плоскости являются точка и прямая.

Вопрос 3. Как обозначаются точки и прямые?
Ответ. Точки обозначаются прописными латинскими буквами: A, B, C, D, … . Прямые обозначаются строчными латинскими буквами: a, b, c, d, … .
Прямую можно обозначать двумя точками, лежащими на ней. Например, прямую a на рисунке 4 можно обозначить AC, а прямую b можно обозначить BC.

Вопрос 4. Сформулируйте основные свойства принадлежности точек и прямых.
Ответ. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и только одну.
Вопрос 5. Объясните, что такое отрезок с концами в данных точках.
Ответ. Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками. Эти точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: «отрезок AB», то подразумевают отрезок с концами в точках A и B.

Вопрос 6. Сформулируйте основное свойство расположения точек на прямой.
Ответ. Из трёх точек на прямой одна и только одна лежит между двумя другими.
Вопрос 7. Сформулируйте основные свойства измерения отрезков.
Ответ. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Вопрос 8. Что называется расстоянием между двумя данными точками?
Ответ. Длину отрезка AB называют расстоянием между точками A и B.
Вопрос 9. Какими свойствами обладает разбиение плоскости на две полуплоскости?
Ответ. Разбиение плоскости на две полуплоскости обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.

В этой статье мы подробно остановимся на одном из первичных понятий геометрии – на понятии прямой линии на плоскости. Сначала определимся с основными терминами и обозначениями. Далее обсудим взаимное расположение прямой и точки, а также двух прямых на плоскости, приведем необходимые аксиомы. В заключении, рассмотрим способы задания прямой на плоскости и приведем графические иллюстрации.

Навигация по странице.

Прямая на плоскости — понятие.

Прежде чем дать понятие прямой на плоскости, следует четко представлять себе что же представляет собой плоскость. Представление о плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).

Если взять хорошо заточенный карандаш и дотронуться его стержнем до поверхности «стола», то мы получим изображение точки. Так мы получаем представление о точке на плоскости .

Теперь можно переходить и к понятию прямой линии на плоскости .

Положим на поверхность стола (на плоскость) лист чистой бумаги. Для того чтобы изобразить прямую линию, нам необходимо взять линейку и провести карандашом линию на сколько это позволяют сделать размеры используемой линейки и листа бумаги. Следует отметить, что таким способом мы получим лишь часть прямой. Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.

Взаимное расположение прямой и точки.

Начать следует с аксиомы: на каждой прямой и в каждой плоскости имеются точки.

Точки принято обозначать большими латинскими буквами, например, точки А и F . В свою очередь прямые линии обозначают малыми латинскими буквами, к примеру, прямые a и d .

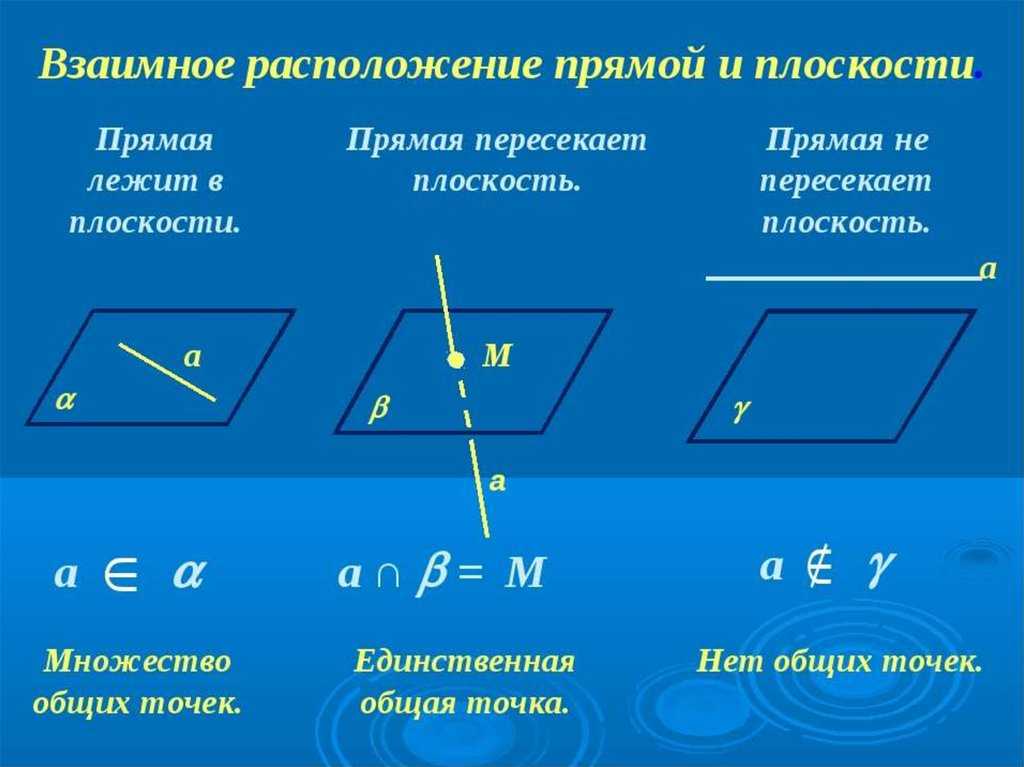
Возможны два варианта взаимного расположения прямой и точки на плоскости : либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).

Для обозначения принадлежности точки некоторой прямой используют символ «». К примеру, если точка А лежит на прямой а , то можно записать . Если точка А не принадлежит прямой а , то записывают .

Справедливо следующее утверждение: через любые две точки проходит единственная прямая.

Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А и В ), можно обозначать двумя этими буквами (в нашем случае прямая АВ или ВА ).

Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.

Множество всех точек, расположенных между двумя заданными на прямой точками, вместе с этими точками называют отрезком прямой или просто отрезком

. Точки, ограничивающие отрезок, называются концами отрезка. Отрезок обозначают двумя буквами, соответствующими точкам концов отрезка. К примеру, пусть точки А и В являются концами отрезка, тогда этот отрезок можно обозначить АВ или ВА . Обратите внимание, что такое обозначение отрезка совпадает с обозначением прямой. Чтобы избежать путаницы, рекомендуем к обозначению добавлять слово «отрезок» или «прямая».

Для краткой записи принадлежности и не принадлежности некоторой точки некоторому отрезку используют все те же символы и . Чтобы показать, что некоторый отрезок лежит или не лежит на прямой пользуются символами и соответственно. К примеру, если отрезок АВ принадлежит прямой а , можно кратко записать .

Следует также остановиться на случае, когда три различных точки принадлежат одной прямой. В этом случае одна, и только одна точка, лежит между двумя другими. Это утверждение является очередной аксиомой. Пусть точки А , В и С лежат на одной прямой, причем точка В лежит между точками А и С .

Тогда можно говорить, что точки А и С находятся по разные стороны от точки В . Также можно сказать, что точки В и С лежат по одну сторону то точки А , а точки А и В лежат по одну сторону от точки С .

Для полноты картины заметим, что любая точка прямой делит эту прямую на две части – два луча . Для этого случая дается аксиома: произвольная точка О , принадлежащая прямой, делит эту прямую на два луча, причем две любые точки одного луча лежат по одну сторону от точки О , а две любые точки разных лучей – по разные стороны от точки О .

Взаимное расположение прямых на плоскости.

Сейчас ответим на вопрос: «Как могут располагаться две прямые на плоскости относительно друг друга»?

Во-первых, две прямые на плоскости могут совпадать .

Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. Действительно, в силу аксиомы, озвученной в предыдущем пункте, через две точки проходит единственная прямая. Иными словами, если через две заданные точки проходят две прямые, то они совпадают.

Во-вторых, две прямые на плоскости могут пересекаться .

В этом случае прямые имеют одну общую точку, которую называют точкой пересечения прямых. Пересечение прямых обозначают символом «», к примеру, запись означает, что прямые а и b пересекаются в точке М . Пересекающиеся прямые приводят нас к понятию угла между пересекающимися прямыми . Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными (рекомендуем статью перпендикулярные прямые, перпендикулярность прямых). Если прямая a перпендикулярна прямой b , то можно использовать краткую запись .

В-третьих, две прямые на плоскости могут быть параллельными.

Прямую линию на плоскости с практической точки зрения удобно рассматривать вместе с векторами. Особое значение имеют ненулевые векторы, лежащие на данной прямой или на любой из параллельных прямых, их называют направляющими векторами прямой . В статье направляющий вектор прямой на плоскости даны примеры направляющих векторов и показаны варианты их использования при решении задач.

Также следует обратить внимание на ненулевые векторы, лежащие на любой из прямых, перпендикулярных данной. Такие векторы называют нормальными векторами прямой . О применении нормальных векторов прямой рассказано в статье нормальный вектор прямой на плоскости .

Когда на плоскости даны три и более прямых линии, то возникает множество различных вариантов их взаимного расположения. Все прямые могут быть параллельными, в противном случае некоторые или все из них пересекаются. При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.

Не будем подробно останавливаться на этом, а приведем без доказательства несколько примечательных и очень часто используемых фактов:

• если две прямые параллельны третьей прямой, то они параллельны между собой;
• если две прямые перпендикулярны третьей прямой, то они параллельны между собой;
• если на плоскости некоторая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую прямую.

Способы задания прямой на плоскости.

Сейчас мы перечислим основные способы, которыми можно задать конкретную прямую на плоскости. Это знание очень полезно с практической точки зрения, так как на нем основывается решение очень многих примеров и задач.

Во-первых, прямую можно задать, указав две точки на плоскости.

Действительно, из аксиомы, рассмотренной в первом пункте этой статьи, мы знаем, что через две точки проходит прямая, и притом только одна.

Если в прямоугольной системе координат на плоскости указаны координаты двух несовпадающих точек, то есть возможность записать уравнение прямой, проходящей через две заданные точки .

Во-вторых, прямую можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна. Этот способ справедлив, так как через данную точку плоскости проходит единственная прямая, параллельная заданной прямой. Доказательство этого факта проводилось на уроках геометрии в средней школе.

Если прямую на плоскости задать таким способом относительно введенной прямоугольной декартовой системы координат, то есть возможность составить ее уравнение. Об этом написано в статье уравнение прямой, проходящей через заданную точку параллельно заданной прямой .

В-третьих, прямую можно задать, если указать точку, через которую она проходит, и ее направляющий вектор.

Если прямая линия задана в прямоугольной системе координат таким способом, то легко составить ее каноническое уравнение прямой на плоскости и параметрические уравнения прямой на плоскости .

Четвертый способ задания прямой заключается в том, что следует указать точку, через которую она проходит, и прямую, которой она перпендикулярна. Действительно, через заданную точку плоскости проходит единственная прямая, перпендикулярная данной прямой. Оставим этот факт без доказательства.

Наконец, прямую на плоскости можно задать, указав точку, через которую она проходит, и нормальный вектор прямой.

Если известны координаты точки, лежащей на заданной прямой, и координаты нормального вектора прямой, то есть возможность записать общее уравнение прямой .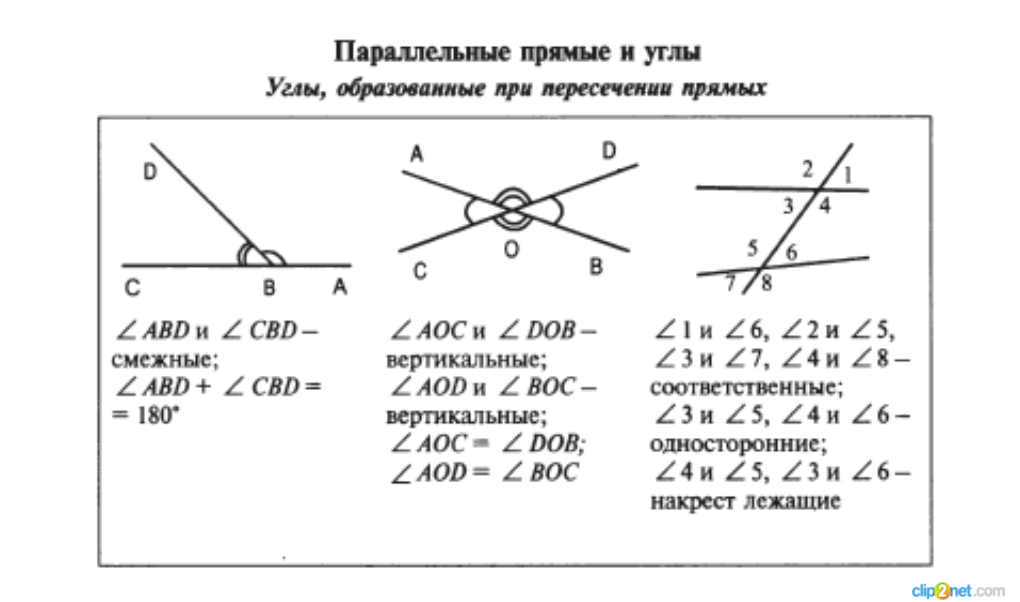

Список литературы.

• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
• Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
• Ильин В.А., Позняк Э.Г. Аналитическая геометрия.

Copyright by cleverstudents

Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.

Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

точка A, точка B, точка C

A B C

точка 1, точка 2, точка 3

1 2 3

Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие? A A A

Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет

Обозначается строчными (маленькими) латинскими буквами

линия a, линия b, линия c

a b c

Линия может быть

1. замкнутой, если её начало и конец находятся в одной точке,
2. разомкнутой, если её начало и конец не соединены

замкнутые линии

разомкнутые линии

Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.

1. самопересекающейся
2. без самопересечений

самопересекающиеся линии

линии без самопересечений

1. прямой
2. ломанной
3. кривой

прямые линии

ломанные линии

кривые линии

Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны

Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны

Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой

прямая линия a

a

прямая линия AB

B A

Прямые могут быть

1. пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
   • перпендикулярными, если пересекаются под прямым углом (90°).
2. параллельными, если не пересекаются, не имеют общей точки.

параллельные линии

пересекающиеся линии

перпендикулярные линии

Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону

У луча света на картинке начальной точкой является солнце

солнышко

Точка разделяет прямую на две части — два луча A A

Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче

луч a

a

луч AB

B A

Лучи совпадают, если

1. расположены на одной и той же прямой,
2. начинаются в одной точке,
3. направлены в одну сторону

лучи AB и AC совпадают

лучи CB и CA совпадают

C B A

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.

Длина отрезка — это расстояние между его начальной и конечной точками

Через одну точку можно провести любое число линий, в том числе прямых

Через две точки — неограниченное количество кривых, но только одну прямую

кривые линии, проходящие через две точки

B A

прямая линия AB

B A

От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B A ✂

Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок

отрезок AB

B A

Задача: где прямая , луч , отрезок , кривая ?

Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°

Длинный отрезок «поломали» на несколько коротких

Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.

Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.

Обозначается ломанная перечислением всех её вершин.

ломанная линия ABCDE

вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E

звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE

звено AB и звено BC являются смежными

звено BC и звено CD являются смежными

звено CD и звено DE являются смежными

A B C D E 64 62 127 52

Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305

Задача: какая ломанная длиннее , а у какой больше вершин ? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.

Многоугольник — это замкнутая ломанная линия

Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.

Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.

Обозначается многоугольник перечислением всех его вершин.

замкнутая ломанная линия, не имеющая самопересечения, ABCDEF

многоугольник ABCDEF

вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F

вершина A и вершина B являются соседними

вершина B и вершина C являются соседними

вершина C и вершина D являются соседними

вершина D и вершина E являются соседними

вершина E и вершина F являются соседними

вершина F и вершина A являются соседними

сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF

сторона AB и сторона BC являются смежными

сторона BC и сторона CD являются смежными

сторона CD и сторона DE являются смежными

сторона DE и сторона EF являются смежными

сторона EF и сторона FA являются смежными

A B C D E F 120 60 58 122 98 141

Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599

Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.

Прямая / Геометрия / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Геометрия
5. Прямая

Понятие прямой

Если отрезок АВ продолжить в обе стороны, то получим геометрическую фигуру, которая называется прямая.

Обозначается и произносится: прямая АВ (или прямая ВА).

Про точки А и В говорят, что они лежат на прямой (принадлежат прямой).

Отрезок АВ лежит на прямой АВ.

Через любые две точки на плоскости проходит единственная прямая (одна и только одна прямая).

На рисунке также изображена прямая АВ (точки не отмечены).

Часто прямые обозначают одной строчной буквой латинского алфавита (a, b, c,.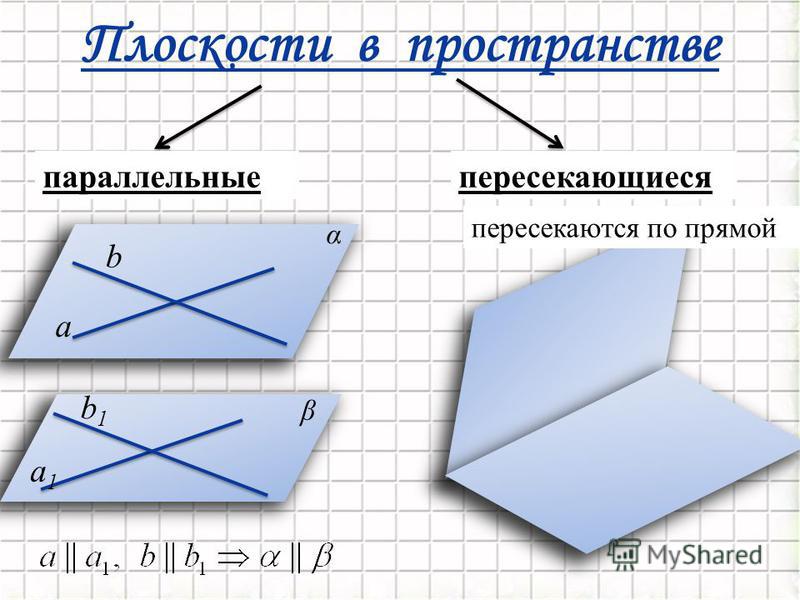 .., m, n,…):

Читают: прямая m, прямая n.

Прямая не имеет начала и не имеет конца.

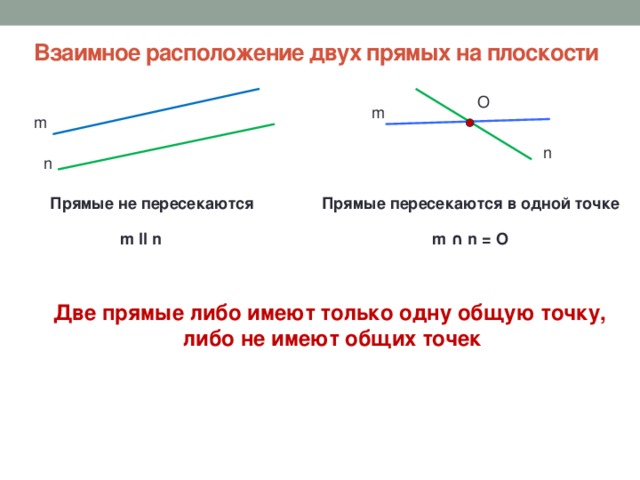
Пересекающиеся прямые

На рисунке прямые a и b имеют одну общую точку О. Говорят, что прямые a и b пересекаются в точке О. 

Сами прямые называются пересекающимися (a и b – пересекающиеся прямые).

Любые две пересекающиеся прямые имеют только одну общую точку.

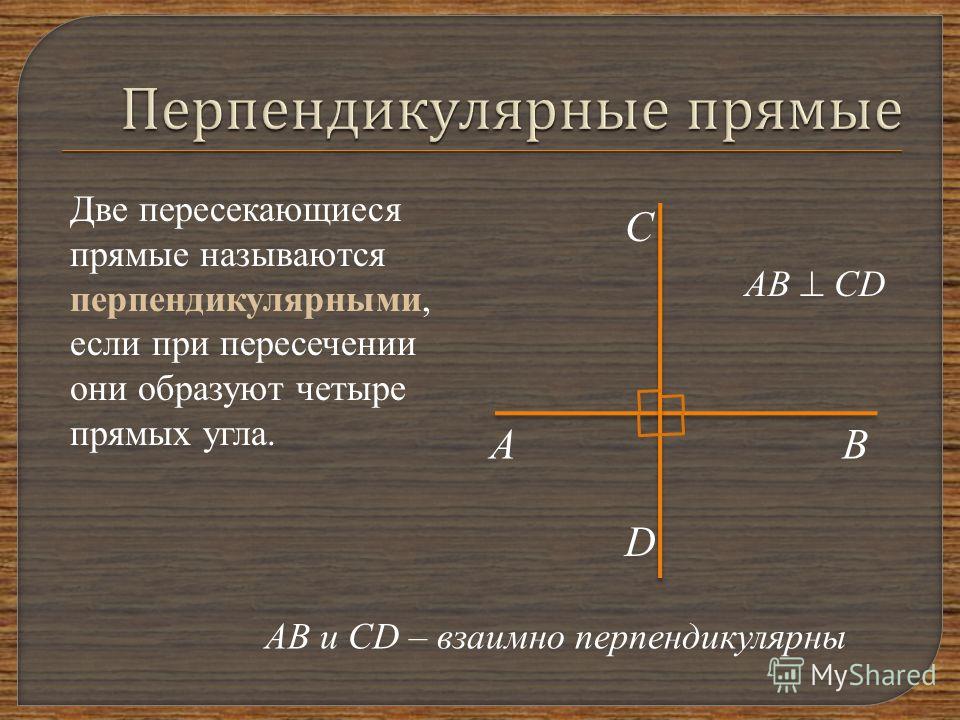
Перпендикулярные прямые

Две прямые называются перпендикулярными, если они пересекаются под прямым углом (угол между ними равен 90º).

На чертежах такой угол отмечают значком прямого угла «». 

Для обозначения перпендикулярных прямых используют знак перпендикулярности «⏊«. 

Записывают: с⏊d; 

Читают: прямая с перпендикулярна прямой d.

Перпендикулярные прямые называют взаимно перпендикулярными, потому, что верны выражения «прямые c и d перпендикулярны» или «прямые d и с перпендикулярны».

 

Советуем посмотреть:

Отрезок

Ломаная

Четырехугольники

Единицы измерения площадей. Свойства площадей

Прямоугольник, его периметр и площадь. Ось симметрии фигуры

Квадрат. Периметр и площадь квадрата.

Многоугольники. Правильные многоугольники. Равенство фигур.

Плоскость

Луч

Шкалы и координаты

Прямоугольный параллелепипед. Пирамида.

Объем прямоугольного параллелепипеда

Куб. Площадь поверхности куба

Куб. Объем куба

Угол. Обозначение углов

Прямой и развернутый угол

Чертежный треугольник

Измерение углов. Транспортир. Виды углов

Треугольник и его виды

Окружность, круг, шар

Цилиндр, конус

Отрезок-xx

Геометрия

Правило встречается в следующих упражнениях:

5 класс

Задание 75, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 81, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 82, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 103, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 276, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 443, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 697, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 93, Мерзляк, Полонский, Якир, Учебник

Номер 3, Мерзляк, Полонский, Якир, Учебник

Номер 4, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 724, Мерзляк, Полонский, Якир, Учебник

Номер 1282, Мерзляк, Полонский, Якир, Учебник

Номер 1283, Мерзляк, Полонский, Якир, Учебник

Номер 1284, Мерзляк, Полонский, Якир, Учебник

Номер 1286, Мерзляк, Полонский, Якир, Учебник

Номер 1287, Мерзляк, Полонский, Якир, Учебник

Номер 1289, Мерзляк, Полонский, Якир, Учебник

Номер 4, Мерзляк, Полонский, Якир, Учебник

Номер 7, Мерзляк, Полонский, Якир, Учебник

Задание 1544, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

---

Пересекающиеся линии — свойства, примеры, значение

LearnPracticeDownload

Пересекающиеся линии — это линии, которые встречаются или пересекают друг друга на плоскости.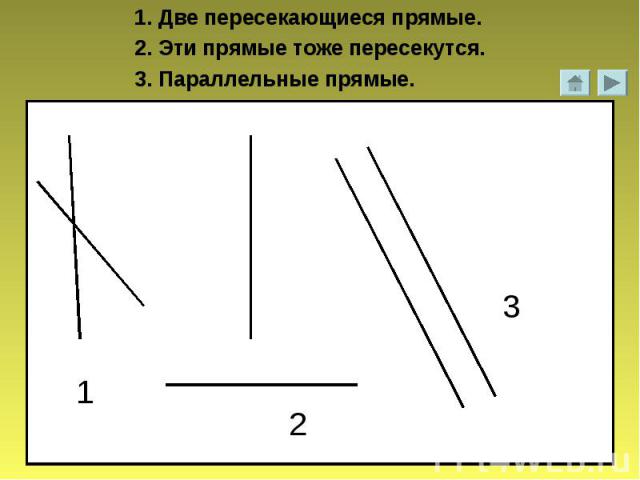 С другой стороны, когда две или более прямых не пересекаются ни в одной точке, они называются непересекающимися прямыми. Давайте узнаем больше о пересекающихся и непересекающихся линиях в этой статье.

1.	Что такое пересекающиеся линии?
2.	Свойства пересекающихся линий
3.	Непересекающиеся линии
4.	Свойства непересекающихся линий
5.	Часто задаваемые вопросы о пересекающихся и непересекающихся линиях

Что такое пересекающиеся линии?

Когда две или более линий встречаются в одной точке, они называются пересекающихся линий . Точка, в которой они пересекаются, называется точкой пересечения. Обратите внимание на следующий рисунок, на котором показаны две пересекающиеся линии «a» и «b» и точка пересечения «O».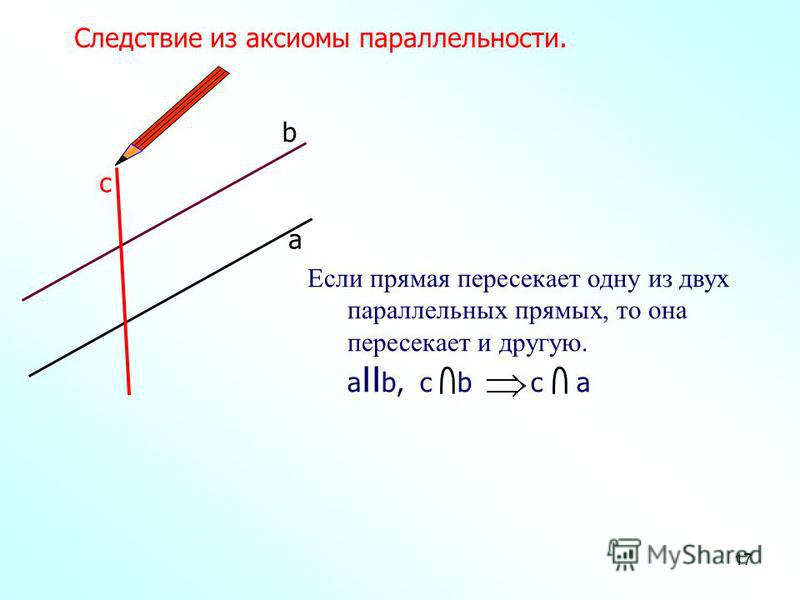

Свойства пересекающихся линий

В следующих пунктах перечислены свойства пересекающихся линий, которые помогают нам легко их идентифицировать.

• Пересекающиеся линии встречаются в одной точке, они не могут пересекаться более чем в одной точке.
• Пересекающиеся линии встречаются друг с другом под любым углом, который больше 0° и меньше 180°.

Непересекающиеся линии

Когда две или более линий не пересекаются друг с другом, они называются непересекающимися линиями. Обратите внимание на следующий рисунок двух непересекающихся параллельных линий «a» и «b», которые показывают перпендикулярное расстояние, обозначенное «c» и «d».

Свойства непересекающихся линий

В следующих пунктах перечислены свойства непересекающихся линий, которые помогают нам легко их идентифицировать.

• Непересекающиеся прямые никогда не пересекаются и не имеют общих точек. Их также называют параллельными линиями.
• Расстояние между непересекающимися линиями всегда одинаково.
• Длина любого общего перпендикуляра, проведенного между двумя непересекающимися прямыми, всегда одинакова.

☛ Статьи по теме

• Линии и углы
• Линейный сегмент
• Формула параллельных линий
• Формула перпендикулярных линий
• Разница между линией и линейным сегментом

 

Примеры пересекающихся линий

1. Пример 1: Что касается пересекающихся и непересекающихся линий, ответьте на следующие вопросы, опираясь на приведенный ниже рисунок.

   1) Линии KL и MN являются ____ линиями.
   2) Прямые CD и AB перпендикулярны друг другу?
   3) Назовите любые две пары непересекающихся прямых.

   Решение:

   1) Линии KL и MN пересекаются с линиями.
   2) Нет, прямые CD и AB не перпендикулярны друг другу. Это непересекающиеся, параллельные линии.
   3) АВ || КД и ЭФ || CD. Следовательно, это непересекающиеся прямые.

2. Пример 2: Определите пару линий, приведенных ниже, как пересекающиеся или непересекающиеся линии.

   
   Решение:

   Согласно направлению линий, если такие линии продолжить дальше, они пересекутся в одной точке. Следовательно, данная пара прямых является пересекающимися прямыми.

3. Пример 3: Приведите любые два примера пересекающихся и непересекающихся прямых из реальной жизни.

   Решение:

   Ниже приведены два примера пересекающихся линий:

   Перекрестки: Когда две прямые дороги встречаются в одной точке, они образуют пересекающиеся линии.

   Ножницы: Ножницы имеют два конца, и оба конца образуют пересекающиеся линии.

   Ниже перечислены два примера непересекающихся линий:

   Линейка (шкала): Противоположные стороны линейки являются непересекающимися линиями.

   Рельсы железнодорожного пути: Рельсы железнодорожного пути, параллельные друг другу, являются непересекающимися линиями.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запись на бесплатный пробный урок

Практические вопросы по пересекающимся и непересекающимся линиям

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о пересекающихся линиях

Что такое пересекающиеся линии в геометрии?

Когда две или более линий пересекаются на плоскости, они называются пересекающимися линиями .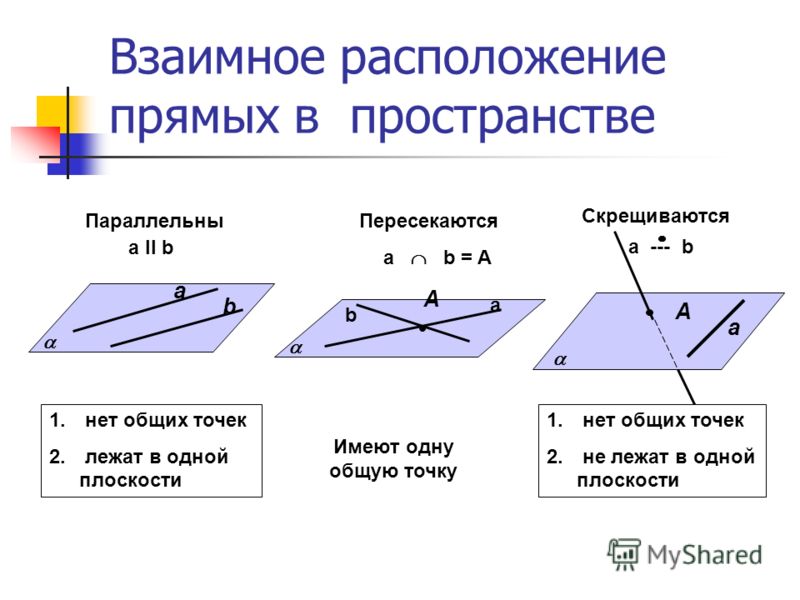 Точка, в которой они пересекаются, называется точкой пересечения.

В чем разница между перпендикулярными и пересекающимися линиями?

Когда пересекающиеся линии пересекаются друг с другом, нет определенного угла, под которым они встречаются, это может быть любой угол. Однако перпендикулярные прямые всегда пересекают друг друга под прямым углом (90°). Другими словами, все перпендикулярные прямые являются пересекающимися прямыми, но не все пересекающиеся прямые могут быть перпендикулярными прямыми.

Что такое параллельные, перпендикулярные и пересекающиеся линии?

Параллельные прямые никогда не пересекаются и всегда находятся на одинаковом расстоянии друг от друга, в то время как пересекающиеся прямые пересекаются и имеют общую точку, известную как точка пересечения. Перпендикулярные прямые — это те пересекающиеся прямые, которые пересекают друг друга под углом 90°.

Какие пересекающиеся линии не являются перпендикулярными?

Некоторые линии пересекаются, но не обязательно перпендикулярны друг другу.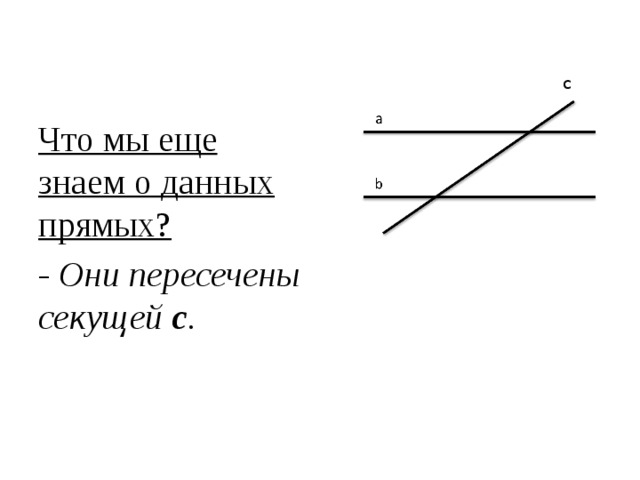 Такие линии сходятся под любым углом, который больше 0° и меньше 180°.

Примеры пересекающихся линий?

Несколько примеров пересекающихся линий приведены ниже:

• Линии буквы «X» образуют пересекающиеся линии. Это прекрасный пример для представления пересекающихся линий.
• Символ сложения (+).
• Стрелки часов.

Какие углы образуются при пересечении прямых?

При пересечении двух прямых они образуют вертикально противоположные углы (вертикальные углы). Вертикально противоположные углы противоположны друг другу и равновелики. Пересекающиеся линии могут пересекаться или пересекаться друг с другом под любым углом от 0° до 180°. Если любые две пересекающиеся прямые пересекаются под углом 90°, они называются перпендикулярными линиями.

Каковы примеры непересекающихся линий?

Ниже приведены несколько примеров непересекающихся линий:

• Противоположные стороны линейки (шкалы) являются непересекающимися линиями.
• Противоположные стороны прямоугольника.

Что вы подразумеваете под точкой пересечения пересекающихся линий?

Когда любые две прямые пересекаются в одной точке, они называются пересекающимися прямыми. Общая точка, в которой они пересекаются, называется точкой пересечения.

Загрузить БЕСПЛАТНЫЕ учебные материалы

Загрузить рабочие листы по геометрии

Рабочие листы по математике и визуальный учебный план

Пересекающиеся линии: определение, свойства

Пересекающаяся линия является прямой и считается структурой с незначительной шириной или глубиной. Из-за неопределенной длины линии у нее нет концов. Однако, если у него есть конечная точка, он считается отрезком линии. Его можно определить по наличию двух стрелок, по одной на обоих концах линии. Теперь, когда понятия линии и отрезка ясны, будет легко понять больше о пересекающихся линиях.

Определение пересекающихся линий  

На плоскости пересекающиеся прямые — это те, которые пересекаются или встречаются.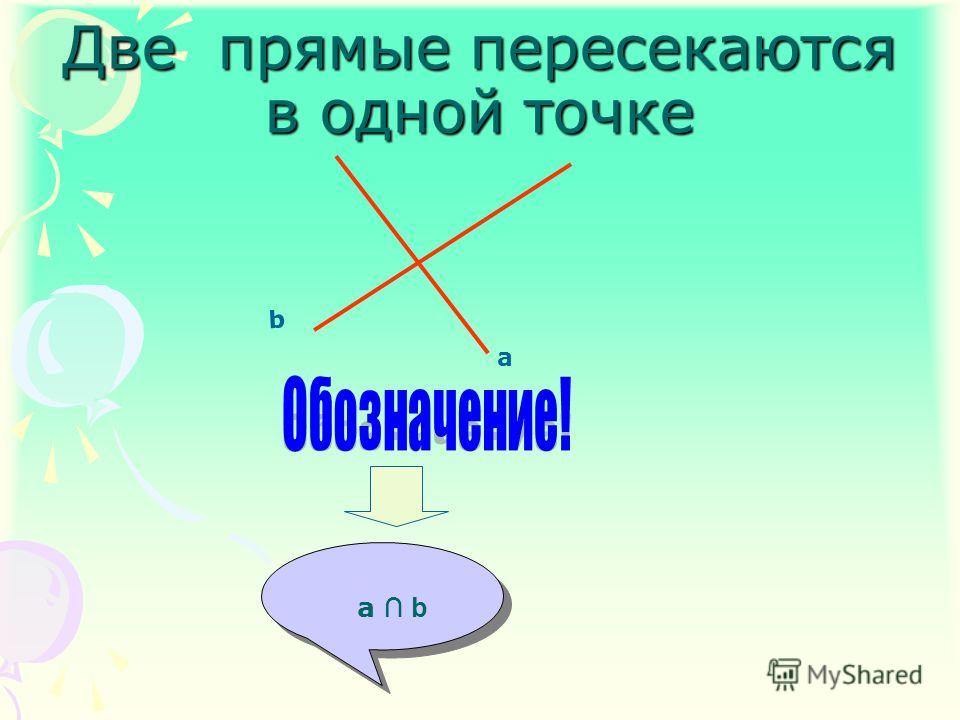 С другой стороны, две или более прямых называются непересекающимися, если они никогда не пересекаются. Давайте узнаем больше о непересекающихся и пересекающихся линиях в этой статье.

Пересекающиеся линии образуются, когда две или более линий пересекают друг друга на плоскости. Пересекающиеся линии имеют общую точку, известную как точка пересечения, которая существует на всех пересекающихся линиях.

Значение пересечения  

Пересечение относится к месту или области, где два или более объекта (например, улицы) сходятся, пересекаясь, набор элементов, общих для двух или более наборов наборов точек, которые являются общими для двух геометрических объектов. конфигурации.

Какие бывают два типа линий?

С точки зрения геометрии линия представляет собой одномерную структуру, равную расстоянию между двумя точками. Линия обычно прямая и может не иметь конечной точки.

Если линия имеет начальную и конечную точки, она называется отрезком линии.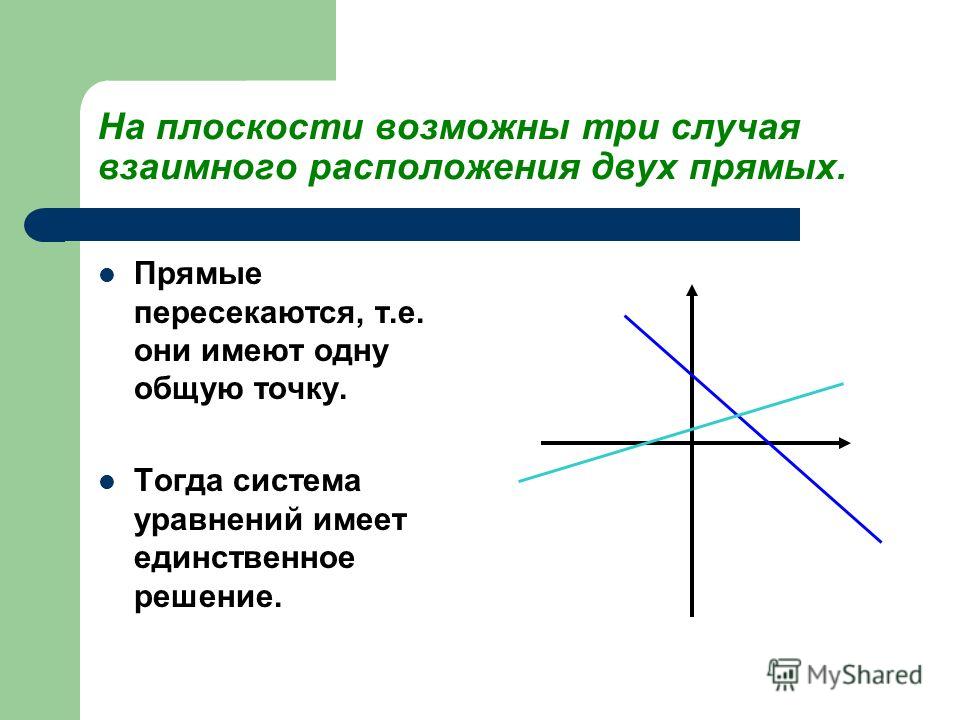 Он имеет определенную длину и не простирается бесконечно.

С другой стороны, линия — это бесконечная фигура, которую невозможно ни нарисовать, ни воспринять. Теперь, говоря о отрезках линий, линии, которые имеют определенную длину, могут быть двух типов –

• Непересекающиеся линии

Непересекающиеся линии относятся к линиям, которые не пересекаются и не касаются друг друга. Это означает, что эти линии не пересекаются и поэтому называются непересекающимися линиями.

Прекрасным примером непересекающихся линий могут быть две параллельные линии рядом друг с другом. Эти параллельные линии могут проходить вперед или назад. Однако они всегда находятся на расстоянии друг от друга, без точки пересечения.

• Пересекающиеся прямые

Определить, является ли данная фигура пересекающейся линией, можно только в том случае, если имеется более одной прямой. Невозможно показать пересечения только одной линией.

Пересекающиеся линии имеют точку пересечения. Эта точка пересечения может быть одной или несколькими в зависимости от количества пересекающихся линий.

Чтобы узнать, что такое пересекающиеся линии, прочтите следующие разделы.

Что такое пересекающиеся линии?

Теоретически линия определяется как фигура, имеющая только одно измерение. Кроме того, линии имеют бесконечную длину, которая, как правило, неизмерима. Однако для изображения линии используется отрезок линии. Несмотря на то, что отрезок линии выглядит как линия, он имеет две конечные точки. Это означает, что отрезок может быть измерен и имеет конечную точку.

Что такое пересекающиеся линии? Два заданных отрезка называются пересекающимися прямыми, если они имеют точку пересечения.

Точкой пересечения называется точка, в которой встречаются два или более отрезка прямой. Эти линии не параллельны друг другу и, следовательно, пересекаются при движении вперед. Видно, что когда два непараллельных отрезка нарисованы конечным образом, они пересекаются в некоторой точке.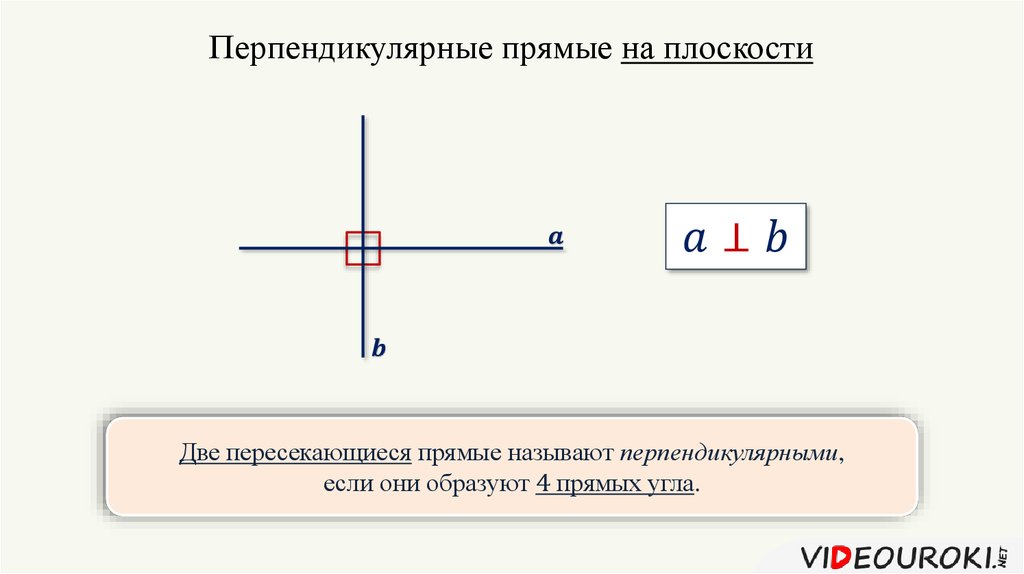 В этой единственной точке происходит пересечение.

Каковы свойства пересекающихся линий?

Чтобы больше узнать о пересекающихся линиях, можно начать с изучения геометрических свойств пересекающихся линий.

Ниже приведены свойства пересекающихся линий :

• Для образования точки пересечения необходимы два или более отрезка линии.
• Возможно, пересечение двух или более отрезков прямой имеет только одну точку пересечения.
• Сегменты линии должны иметь хотя бы одну точку, в которой они пересекаются друг с другом. Эта конкретная точка является точкой пересечения.
• Точка пересечения является общей точкой всех пересекающихся отрезков.
• Два пересекающихся сегмента линии могут иметь только одну точку пересечения.
• Независимо от угла две прямые не могут пересекаться более чем в одной точке.
• Две пересекающиеся прямые не могут быть параллельны друг другу.
• Сегменты линии, пересекающиеся более чем в одной точке, обычно не имеют прямого пути.
• Две линии могут иметь более одной точки пересечения только в том случае, если одна из линий изогнута.
• Точка пересечения обычно образует угол между двумя пересекающимися линиями.
• Две линии пересекаются в точке, где угол составляет от 0° до 180°.

Как найти пересечение двух линий?

Чтобы понять, как найти пересечение двух прямых, нужно взглянуть на две непараллельные прямые. Ниже приведено изображение двух непараллельных прямых, пересекающихся в заданной точке.

Пересекающиеся линии

Можно легко определить точку пересечения двух линий, просто взглянув на них. Когда два отрезка пересекаются друг с другом, они считаются двумя пересекающимися прямыми. Это помогает понять, как найти пересечение двух линий.

Пересечение двух линий зависит от следующих факторов :

• Линии не должны быть параллельны друг другу.
• Линии в данной точке пересечения должны быть прямыми.
• Точка пересечения должна обеспечивать пересечение двух прямых в точке с углом между двумя пересекающимися отрезками прямой.
• Если две непараллельные прямые не имеют точки пересечения, это не означает, что они не пересекаются. Это означает, что когда эти два отрезка линии проведены вперед, они встретятся в определенной точке, даже если это большое расстояние.

Как выглядит пересечение двух линий?

Определить, пересекаются ли заданная фигура из двух отрезков, довольно просто. Две пересекающиеся линии могут напоминать букву T или V. В большинстве случаев две пересекающиеся линии образуют букву X, когда пересекаются друг с другом.

Пересекающиеся линии и угол

Это изображение означает, что две пересекающиеся линии встречаются только в одной точке. Поняв приведенное выше изображение, легко определить пересекающиеся линии в следующий раз, когда вы его увидите.

Два непараллельных отрезка линии могут не пересекаться. Однако они все же могут иметь точку пересечения, например, букву V.

Две пересекающиеся линии похожи на букву T, когда они перпендикулярны друг другу. Когда две линии настроены перпендикулярно друг другу, это означает, что они образуют угол 90 ° в точке пересечения. Это означает, что перпендикулярные линии также являются пересекающимися линиями, которые образуют только прямые углы.

Перпендикулярные линии

Как определить, будут ли пересекаться две прямые?

Из вышеприведенных пояснений видно, что параллельные прямые не пересекаются друг с другом. Однако даже малейший наклон любой из линий может привести к пересечению.

Два заданных отрезка могут показаться параллельными, но они все же могут иметь точку пересечения, если их рисовать вперед или назад.

В некоторых случаях, даже если есть два непараллельных отрезка, они считаются непересекающимися линиями, поскольку между ними большое расстояние. Неуместно говорить, что две линии не могут пересекаться только потому, что они далеко друг от друга. Этим линиям может потребоваться большое расстояние, чтобы пересечь путь друг друга. Однако их нельзя назвать непересекающимися линиями.

Две прямые пересекутся, если –

• Они не параллельны друг другу.
• Они перпендикулярны друг другу.

Как две прямые могут не пересекаться?

Определенные критерии определяют пересечение двух линий. Если две линии не удовлетворяют этим критериям, они не считаются пересекающимися линиями. Ниже приведены причины, определяющие, когда два заданных отрезка прямой не пересекаются.

Две прямые не могут пересекаться друг с другом при проведении вперед, если они имеют :

• Конечные точки
• Бесконечное расстояние между ними
• Они параллельны друг другу
• Они не параллельны, но имеют определенную длину и не пересекаются друг с другом
• Являются ли непараллельные отрезки с промежутком между ними

Какие есть примеры пересекающихся прямых в реальной жизни?

Пересечение линий — типичный пример повседневной жизни. Даже если на них можно не обращать внимания, они окружены линиями пересечения.

Например, перекресток — это место, где две дороги сходятся в одной точке. Этот пример означает, что две дороги не параллельны друг другу. Кроме того, эти две дороги образуют определенный угол в точке их пересечения.

Другой пример — ножницы. Два лезвия ножниц подобны двум пересекающимся линиям. Если их развести, два ножа образуют угол, когда две линии пересекаются в точке пересечения.

Примеры пересекающихся линий  

Пример. Приведите реальные примеры непересекающихся и пересекающихся линий.  

Ниже приведены два примера пересекающихся линий:  

1. Перекрестки образуются, когда две прямые дороги пересекаются в одной точке.
2. Ножницы: ножницы имеют два конца, которые образуют пересекающиеся линии.
3. Часы: Пересекающиеся линии образованы двумя стрелками, проходящими через общую точку часов.
4. A, T, L, M: Некоторые буквы английского алфавита также являются примерами пересекающихся линий.
5. Края ноутбука: Смежные края ноутбука пересекаются под прямым углом. В результате речь идет о пересекающихся линиях.

Вот два примера непересекающихся линий:  

1. Масштаб: противоположные стороны линейки — непересекающиеся линии.
2. Рельсы железнодорожного пути: Рельсы железнодорожного пути, параллельные друг другу, являются непересекающимися линиями.
3. Крикетные калитки расположены таким образом, что никогда не пересекаются; таким образом, они являются примером непересекающейся линии.
4. Провода электрических опор: Поскольку все провода электрических опор имеют одинаковую длину, они представляют собой прекрасный пример непересекающихся линий.
5. Лестница является примером непересекающейся линии, потому что две ее стороны никогда не пересекаются.

Заключение

Пересекающиеся линии — удобный способ изучения линий и точек их пересечения.