Как определить угол наклона в градусах: Как определить угол наклона уже готовой кровли

Как определить угол наклона уже готовой кровли

Расчет уклона кровли — обязательный этап проектирования дома. От угла наклона скатов зависят снеговая и ветровая нагрузки на крышу, которые через стены передаются на фундамент.

Но есть ситуации, когда необходимо узнать фактический уклон уже готовой кровли. Например, при реконструкции крыши с заменой кровельного материала более тяжелым или при установке солнечных панелей на скатах. Ниже — два способа, как определить угол наклона в этом случае.

Определить уклон ската можно либо с помощью специальных инструментов, либо воспользовавшись базовыми законами геометрии. Первый способ проще и точнее, второй доступен всегда — главное, чтобы была рулетка, а остальные инструменты не важны.

Инструментальный метод

Чтобы определить угол наклона кровли просто и быстро, используйте специальные измерительные инструменты:

• угломеры, которые измеряют угол между двумя «плечами» инструмента;
• уклономеры, которые показывают уклон кровли относительно гравитационного поля Земли.

Угломеры для расчета уклона кровли

Угломер — чрезвычайно простой, но эффективный инструмент. Он бывает механическим и электронным.

Механический угломер состоит из планок, которые соединены друг с другом с одного края, и шкалы между ними. Со второй стороны концы планок свободные и могут вращаться вокруг места соединения. Шкала показывает, на какой угол две части угломера повернуты друг относительно друга. Конструкция настолько простая, что, при необходимости, механический угломер можно даже сконструировать самостоятельно из двух линеек и транспортира.

Электронные угломеры по принципу работы точно такие же. Есть только одно отличие: шкала для определения угла между плечами инструмента заменена специальным датчиком, который считывает положение планок. Результат отображается на небольшом экране.

Механические угломеры — более надежный инструмент: нет риска, что откажет датчик или экран. Но с точки зрения удобства электронные устройства выигрывают.

Особенно при измерении под крышей, где часто недостаточно хорошее освещение.

Как определить угол наклона кровли с помощью угломера:

• одну из планок плотно прижмите к стойке, подпирающей коньковую балку, или к самому коньку;
• вторую планку прижмите к нижней кромке стропильной ноги;
• запишите результат измерений и повторите их для разных стропил 8-10 раз;
• отбросьте результаты, которые сильно выбиваются из ряда измерений — слишком большие или слишком маленькие;
• для остальных вычислите среднее арифметическое — это и будет угол наклона кровли.

Учитывайте, что для расчета уклона кровли нужно обязательно делать не одно измерение, а несколько, иначе вы рискуете получить некорректные результаты. Приведем пример.

Допустим, вы сделали 10 измерений угломером и получили следующие результаты.

Номер измерения	Угол, градусы
1	25,3
2	28,1
3	25,8
4	25,4
5	27,5
6	25,1
7	25,3
8	30
9	25,5
10	25,2

Второе, пятое и восьмое измерение явно выбиваются из ряда, поэтому их нужно отбросить. Выполняем расчет уклона кровли только по семи измерениям: складываем их и делим на количество. В результате получаем среднее арифметическое — 25,37°. Если бы мы не отфильтровали измерения, то угол бы получился почти на градус больше — 26,32°. И это еще небольшая разница: измерение угла между разными парами стропил и стоек может дать результаты, отличающиеся на 5-7°, иногда даже больше.

Такая разница связана с качеством пиломатериалов, которые обычно используют для стропильной системы. Ее рекомендуют делать из калиброванного леса, то есть из досок, сечение которых примерно одинаковое по всей длине и равно эталонному. Для этого их пропускают через специальный станок — рейсмус, который срезает лишнее и доводит размеры досок до необходимых.

Но калибровка сильно повышает стоимость пиломатериалов, поэтому для большинства стропильных систем с целью экономии берут обычные, некалиброванные доски. Еще и часто недостаточно просушенные. А их ширина даже в сыром виде может отличаться на десятки миллиметров. Причем не у разных досок, а просто по длине одной.

В верхней части стропила выводят в плоскость — нужно же уложить кровельное покрытие, — а в нижней эта разница остается. Она и дает такую погрешность, из-за которой перед тем, как определить угол наклона кровли, нужно сделать множество измерений, чтобы получить более-менее точный результат.

Уклономеры для определения угла наклона ската

Уклономерами пользоваться еще проще, чем угломерами. В основе таких приборов специальные магнитные датчики — инклинометры. Они измеряют угол наклона поверхности, на которой установлены, относительно гравитационного поля Земли. Поэтому это более точный инструмент для расчета уклона кровли.

Чтобы определить угол наклона ската, достаточно просто поставить уклономер на кровельное покрытие или верхнюю кромку стропильной ноги. Независимо от качества пиломатериалов, сверху стропила с обрешеткой выводят в плоскость. Поэтому погрешность будет меньше — для получения точного результата нужно будет повторить измерения 3-4 раза.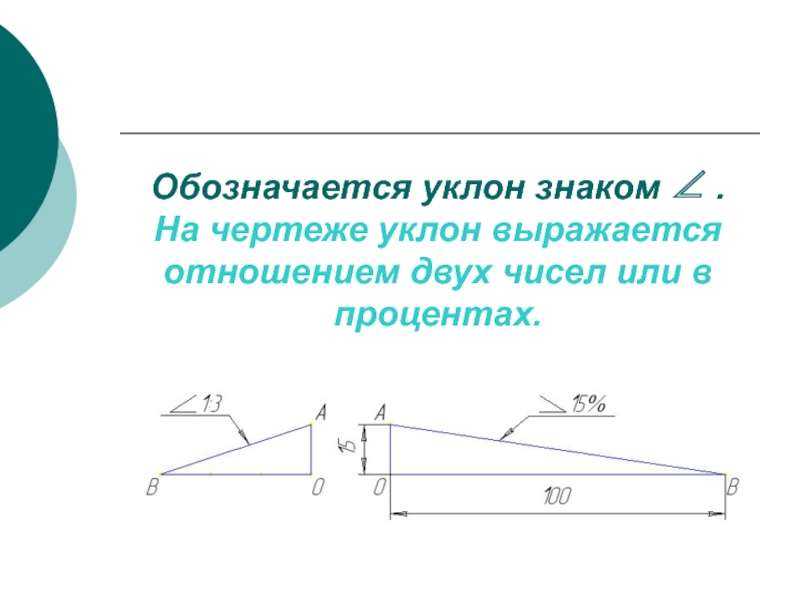

Если установить уклономер на кровельное покрытие нет возможности, его можно прижать к низу стропил. Но тогда измерения нужно будет делать по той же схеме, что и с угломером: 8-10 штук с отбрасыванием крайних значений и расчетом среднего.

Расчет уклона кровли по длине стропил

Угломер или уклономер — это специализированный инструмент, который не всегда есть под рукой, да и покупать его ради одного измерения нет смысла. Поэтому для расчета уклона кровли чаще пользуются базовыми законами геометрии.

Дело в том, что стропило, опорная стойка и перекрытие — это, по сути, стороны прямоугольного треугольника, где стропильная нога — гипотенуза. Следовательно, рассчитать уклон кровли можно по формуле:

α = (h/l)·100%

Здесь:

• α — угол наклона ската, %;
• h — высота крыши, включая коньковую балку, м;
• l — расстояние от середины опорной стойки до карнизного свеса ската, м.

Этот метод дает довольно точный результат, поскольку на него никак не влияют характеристики пиломатериалов.

Но угол получается не в привычных градусах, а в процентах. Поэтому для дальнейших расчетов полученное значение нужно перевести.

Как вычислить угол наклона в градусах? Сделать это можно двумя способами.

Первый способ подходит тем, у кого есть инженерный калькулятор и кто умеет с ним обращаться.  Нужно посчитать арктангенс при делении высоты крыши на длину ската:

α = arctg(h/l)

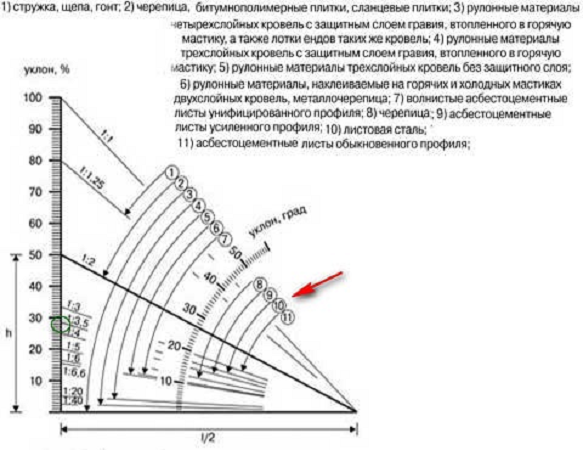
Второй способ проще — нужно вычислить уклон в процентах с помощью следующей схемы.

Просто приложите линейку к схеме: один конец — к крайней точке справа, другой — к тому значению на вертикальной шкале, которое соответствует полученному вами углу наклона в процентах. Тогда место пересечения линейки со скругленной шкалой (транспортиром) покажет уклон в градусах.

Чтобы узнать уклон кровли, можно воспользоваться одним из двух методов:

• инструментальным — измерить его напрямую с помощью уклономера или угломера;
• расчетным — стропила, перекрытие и стойки образуют прямоугольный треугольник, поэтому угол можно рассчитать, разделив высоту крыши до конька на расстояние по полу от карнизного свеса до опор.

Расчетный метод даст уклон в процентах. Как рассчитать угол наклона в градусах? Взять арктангенс от соотношения или воспользоваться специальной схемой для перевода процентов в градусы.

---

Будьте в курсе!

Подпишитесь на новостную рассылку

Как измерить угол наклона крыши в градусах

Главная » Разное » Как измерить угол наклона крыши в градусах

как узнать угол наклона ската в градусах, как рассчитать угол стропил двухскатной крыши, узнать и высчитать

Содержание:

Чтобы крыша здания могла в полной мере выполнять все возложенные на нее функции, необходимо при ее создании учесть ряд параметров. Одним из самых важных параметров крыши является ее уклон, который обеспечивает отвод атмосферных осадков с ее поверхности и влияет на способность выдерживать внешние нагрузки. О том, как посчитать наклон крыши, и пойдет речь в данной статье.

Определение наклона крыши — от чего зависит

Чтобы провести правильный расчет уклона крыши, необходимо учитывать несколько факторов, среди которых сильнее всего выделяются следующие:

1. Ветровые нагрузки. На уклон скатов очень сильно влияет ветер. Чтобы крыша могла нормально сопротивляться его воздействию, нужно правильно подобрать ее угол. При слишком больших углах нагрузка на них будет высокой, но чрезмерное уменьшение угла тоже может быть опасным – пологую кровлю сильным порывом ветра может попросту сорвать.
2. Снеговые и дождевые нагрузки. Со снегом все довольно просто – повышение угла наклона упрощает его схождение с поверхности кровли. При наклоне крыши более 45 градусов снег почти не будет задерживаться на ней. При малом угле наклона кровли может появляться снеговой мешок, который увеличивает нагрузку на крышу. С дождевыми осадками такая же ситуация – если угол наклона кровли будет слишком низким, то вода сможет затекать в стыки или вообще застаиваться на поверхности крыши.

Отталкиваясь от этих факторов, можно рассчитывать угол наклона скатов. Кроме того, перед тем, как рассчитать угол двухскатной крыши, стоит обратить внимание на рекомендуемые показатели: для местности с сильными ветрами подойдет уклон в 15-20 градусов, а в остальных случаях оптимальная величина уклона составляет 35-40 градусов. Разумеется, нужно понимать, что расчет двухскатной крыши индивидуален, и выбирать усредненные показатели просто так нежелательно.

Методика проведения расчетов

При проектировании крыши нужно в обязательном порядке проводить ряд расчетов, среди которых всегда должен присутствовать расчет угла наклона скатов. Данный параметр напрямую влияет на конструкцию крыши: при увеличении наклона снижается снеговая нагрузка, но увеличивается воздействие ветра, поэтому стропильную систему приходится дополнительно усиливать. Для обустройства скатов под большим углом требуется еще и большее количество материалов, что негативно сказывается на стоимости строительства.

Перед тем, как узнать градус наклона крыши, нужно рассчитать эксплуатационную нагрузку на крышу, для чего требуется два параметра:

• Общую массу кровельной конструкции;
• Пиковые уровни снежных осадков, свойственные региону, где проходит строительство.

Упрощенный алгоритм расчетов сводится к следующим действиям:

• Сначала нужно определить вес одного квадратного метра кровельного пирога;
• Полученное значение умножается на общую площадь кровли;
• Масса кровли умножается на коэффициент 1,1.

Пример расчета уклона кровли в градусах

Чтобы понять, как высчитать угол крыши, стоит рассмотреть процесс расчетов на конкретном примере. Для примера будут взяты следующие данные: обрешетка имеет толщину 2,5 см, один квадратный метр кровли весит 15 кг, в качестве теплоизоляционного материала используется утеплитель толщиной 10 см, квадратный метр которого имеет вес 10 кг, а для покрытия используется ондулин с весом 3 кг на квадратный метр.

Расчет ската крыши проводится в соответствии с описанной выше методикой. Подстановка имеющихся данных приводит к следующему выражению: (15+10+3)х1,1 = 30,8 кг/кв.м. Полученная величина вполне допустима – среднестатистическая нагрузка на крышу жилых зданий составляет немногим меньше 50 кг/кв.м. Кроме того, в формуле присутствует коэффициент 1,1, который немного увеличивает фактический вес кровельной конструкции и позволяет в дальнейшем заменить кровельное покрытие на более тяжелое.

Как узнать угол наклона крыши

Между уклоном кровельных скатов и снежной нагрузкой имеется прямая зависимость. Если угол наклона крыши меньше 25 градусов, то коэффициент снежной нагрузки равен 1, а при углах, варьирующихся в пределах от 25 до 60 градусов, то этот коэффициент увеличивается до 1,25. Крыша с большим углом наклона не будет подвергаться снежным нагрузкам вообще, поэтому они не учитываются при расчетах.

Чтобы определить угол наклона крыши, нужно воспользоваться таблицей Брадиса и простой методикой: высота кровельной конструкции делится на длину фронтона, разделенную на два, после чего остается найти таблице угол, который соответствует полученному результату.

Высота крыши в коньке определяется следующим образом:

• Первым делом нужно рассчитать ширину пролета;
• Полученная величина делится на 2;
• Чтобы сделать расчет высоты конька, результат предыдущего расчета умножается на коэффициент, соответствующий определенному углу наклона.

На примере реализация такой методики расчета выглядит так: при ширине здания, равной 8 метрам, и 25-градусном уклоне кровли, расчетный коэффициент составляет 0,47.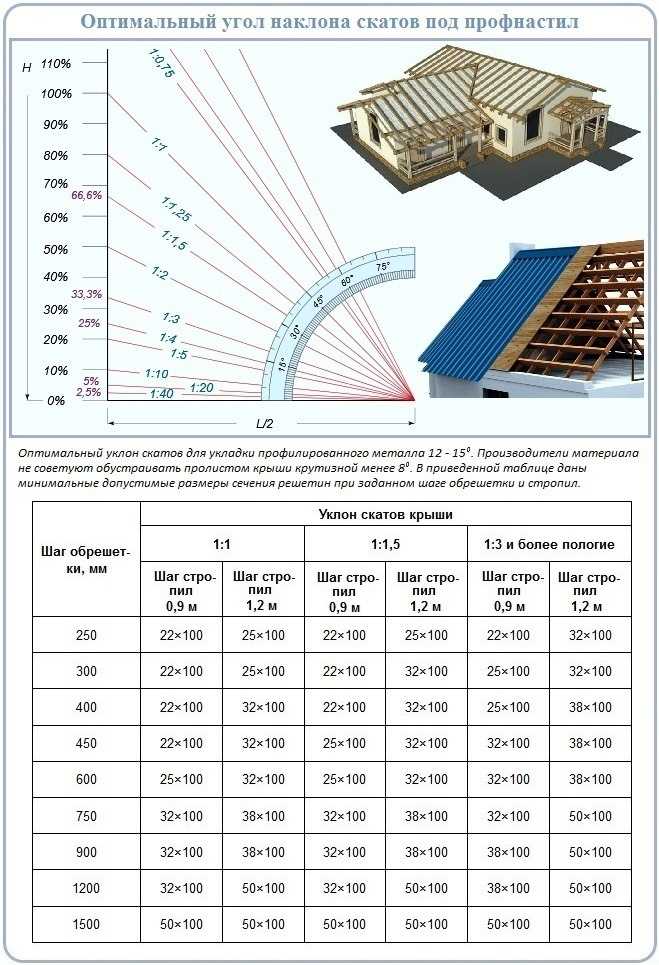 В итоге подстановки значений получается выражение следующего вида: 4х0,47 = 1,88 м. Полученная величина – это высота крыши, соответствующая имеющимся исходным данным.

Выбор кровельного покрытия в зависимости от наклона крыши

На рынке материалы для крыши присутствуют в большом ассортименте, поэтому с выбором подходящего варианта особых проблем не будет. Кровельные покрытия отличаются по характеристикам и возможностям применения, и все их параметры необходимо изучить перед тем, как измерить угол крыши – только в этом случае удастся создать надежную и эффективную конструкцию.

Выбирая материал для кровли, стоит отталкиваться от следующих рекомендаций:

1. Если угол наклона стропил составляет от 2,5 до 10 градусов, то лучше всего подойдут покрытия из каменной крошки или гравия. В первом случае верхний слой покрытия имеет толщину 3-5 мм, а во втором – 10-15 мм.
2. При наклоне более 10 градусов оптимальным вариантом будут крупнозернистые или рулонные материалы, дополненные битумной гидроизоляцией.
3. Для обустройства скатных крыш с углом наклона не более 20 градусов обычно используется профнастил или листовой асбестоцемент. Все швы и стыки между кровельными материалами должны быть обработаны герметиком.
4. Если угол наклона крыши находится в пределах 20-60 градусов, то она чаще всего накрывается металлическими листами. Стыки материалов в данном случае нужно в обязательном порядке герметизировать.

Заключение

Знание того, как узнать угол наклона крыши в градусах, существенно упростит процесс ее проектирования и позволит создать максимально надежную конструкцию, которая сможет хорошо защищать коробку здания от атмосферных осадков, ветра и холода. 

Угол наклона и уклон прямой

Пусть прямая l пересекает ось x в точке A. Угол между положительной осью x и прямой l, измеренный против часовой стрелки, называется углом наклона прямой l.

На приведенном выше рисунке, если θ — угол прямой l, то мы имеем следующие важные моменты.

(i) 0 ° ≤ θ ≤ 180 °

(ii) Для горизонтальных линий θ = 0 ° или 180 ° и для вертикальных линий θ = 90 °

(iii) Если прямая линия изначально проходит вдоль оси x и начинает вращаться вокруг фиксированной точки A на оси x против часовой стрелки и, наконец, совпадает с осью x, тогда угол наклона прямой в исходном положении равен 0 °, а угол наклона прямой линия в конечном положении — 0 °.

(iv) Линии, перпендикулярные оси x, называются вертикальными линиями.

(v) Линии, перпендикулярные оси Y, называются горизонтальными линиями.

(vi) Другие линии, не перпендикулярные ни оси x, ни оси y, называются наклонными линиями.

Угол наклона и уклон линии — Применение

Основное применение угла наклона прямой — это определение уклона.

Если θ — это угол наклона прямой l, то tgθ называется крутизной наклона линии и обозначается буквой «m».

Следовательно, наклон прямой составляет

m = tan θ

для 0 ° ≤ θ ≤ 180 °

Найдем наклон прямой, используя приведенную выше формулу

(i) Для горизонтального линий угол наклона 0 ° или 180 °.

То есть

θ = 0 ° или 180 °

Следовательно, наклон прямой линии равен

m = tan0 ° или tan 180 ° = 0

(ii) Для вертикальных линий угол наклона равен 90 °.

То есть

θ = 90 °

Следовательно, наклон прямой линии равен

m = tan90 ° = Не определено

(iii) Для наклонных линий, если θ острый, то наклон положительный. Если же θ тупой, то наклон отрицательный.

Наклон линии — положительный или отрицательный, ноль или неопределенный

Когда мы визуально смотрим на прямую линию, мы можем легко узнать знак наклона.

Чтобы узнать знак наклона прямой, мы всегда должны смотреть на прямую слева направо.

Это иллюстрируют приведенные ниже цифры.

Практические задачи

Задача 1:

Найдите угол наклона прямой, уклон которой равен 1 / √3.

Решение:

Пусть θ будет углом наклона прямой.

Тогда наклон линии равен

m = tanθ

Дано: Наклон = 1 / √3

Тогда

1 / √3 = tanθ

θ = 30 °

Итак, угол наклона 30 °.

Задача 2:

Если угол наклона прямой составляет 45 °, найдите ее наклон.

Решение:

Пусть θ будет углом наклона прямой.

Тогда наклон линии

m = tanθ

Дано: θ = 45 °

Тогда

m = tan 45 °

m = 1

Итак, наклон равен 1.

Задача 3:

Если угол наклона прямой составляет 30 °, найдите ее наклон.

Решение:

Пусть θ будет углом наклона прямой.

Тогда наклон прямой

m = tanθ

Дано: θ = 30 °

Тогда

m = tan30 °

m = 1 / √3

Итак, наклон равен 1 / √3.

Задача 4:

Найдите угол наклона прямой, имеющей наклон √3.

Решение:

Пусть θ будет углом наклона прямой.

Тогда наклон прямой

m = tanθ

Дано: Наклон = √3

Тогда

√3 = tanθ

θ = 60 °

Итак, угол наклона равен 60 °.

Задача 5:

Найдите угол наклона прямой линии, уравнение которой y = x + 32.

Решение:

Пусть θ будет углом наклона прямой.

Данное уравнение имеет форму пересечения наклона.

То есть

y = mx + b

Сравнивая

y = x + 32

и

y = mx + b,

получаем наклон m = 1.

Мы знаем, что наклон линии

m = tanθ

Тогда

1 = tanθ

θ = 45 °

Итак, угол наклона равен 45 °.

Кроме того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Алгебраные задачи со словами

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямой и обратной вариациям

Проблемы со словами по цене за единицу

Проблемы со словами по цене за единицу

Word задачи по сравнению ставок

Преобразование обычных единиц в текстовые задачи

Преобразование метрических единиц в текстовые задачи

Word задачи по простому проценту

Word по сложным процентам

Word задачи по типам ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами в тригонометрии

Проблемы со словами в процентах

Проблемы со словами о прибылях и убытках

Разметка и разметка Задачи со словами

Задачи с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы со словами о линейных неравенствах

Слово соотношения и пропорции Задачи со словами

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Задачи со словами на возрастах

Проблемы со словами в теореме Пифагора

Процент числового слова pr проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами на сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибылей и убытков

Сокращения в процентах

Сокращения в таблице времен

Сокращения времени, скорости и расстояния

Сокращения соотношения и пропорции

Домен и диапазон рациональных функций

Область и диапазон рациональных функций функции с отверстиями

Графики рациональных функций

Графики рациональных функций с отверстиями

Преобразование повторяющихся десятичных дробей в дроби

Десятичное представление рациональных чисел

Нахождение квадратного корня с использованием long di зрение

Л. Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении 17 в степени 23 на 16

Сумма всех трехзначных чисел, делящихся на 6

Сумма всех трехзначных чисел, делящихся на 7

Сумма всех трехзначных чисел, делящихся на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

.

Внимание! | Cloudflare

Почему я должен заполнять CAPTCHA?

Заполнение CAPTCHA доказывает, что вы человек, и дает вам временный доступ к веб-ресурсу.

Что я могу сделать, чтобы этого не произошло в будущем?

Если вы используете личное соединение, например, дома, вы можете запустить антивирусное сканирование своего устройства, чтобы убедиться, что оно не заражено вредоносными программами.

Если вы находитесь в офисе или в общей сети, вы можете попросить администратора сети запустить сканирование сети на предмет неправильно сконфигурированных или зараженных устройств.

Еще один способ предотвратить появление этой страницы в будущем — использовать Privacy Pass. Возможно, вам потребуется загрузить версию 2.0 прямо сейчас из Магазина дополнений Firefox.

.

Как вычислить опорные углы в градусах

2. Образование
3. Математика
4. Тригонометрия
5. Как вычислить опорные углы в градусах

Мэри Джейн Стерлинг

Найти опорный угол в градусах намного проще, чем пытаться для определения триггерной функции для исходного угла. Для того, чтобы вычислить меру (в градусах) опорного угла для любого заданного угла тета, использовать правила в следующей таблице.

Определение опорных углов в градусах

Квадрант	Мера угла Тета	Мера исходного угла
I	от 0 ° до 90 °	тета
II	от 90 ° до 180 °	180 ° — тета
III	от 180 ° до 270 °	тета — 180 °
IV	от 270 ° до 360 °	360 ° — тета

Найдите опорный угол для 200 градусов:

1. Определите квадрант, в котором находится терминальная сторона.

   Угол в 200 градусов составляет от 180 до 270 градусов, поэтому сторона вывода находится в QIII.

2. Выполните операцию, указанную для этого квадранта.

   Вычтите 180 градусов из угла, который составляет 200 градусов. Вы обнаружите, что 200–180 = 20, поэтому опорный угол составляет 20 градусов.

Теперь найдите опорный угол для 350 градусов:

1. Определите квадрант, в котором находится терминальная сторона.

   Угол в 350 градусов составляет от 270 до 360 градусов, поэтому сторона вывода находится в QIV.

2. Выполните операцию, указанную для этого квадранта.

   Вычтите 350 градусов из угла, который составляет 360 градусов. Вы обнаружите, что 360 — 350 = 10, поэтому угол отсчета составляет 10 градусов.

Иногда угловые размеры не соответствуют диапазонам, указанным в таблице. Например, вам может потребоваться найти опорный угол для отрицательного угла или кратного угла.

Чтобы найти исходный угол для –340 градусов:

1. Определите квадрант, в котором находится терминальная сторона.

   A Угол –340 градусов эквивалентен углу 20 градусов. (Вы получаете положительную угловую меру, добавляя 360 или один полный оборот вокруг начала координат к отрицательной величине.) Конечная сторона 20-градусного угла находится в QI.

2. Выполните операцию, указанную для этого квадранта.

   Углы в первом квадранте являются их собственным опорным углом, поэтому опорный угол составляет 20 градусов.

На другом конце спектра, чтобы найти опорный угол для 960 градусов:

1. Определите квадрант, в котором находится терминальная сторона.

   Угол 960 градусов эквивалентен углу 240 градусов. (Вы получаете эту меру, дважды вычитая 360 из 960). Угол в 240 градусов составляет от 180 до 270 градусов, поэтому его конечная сторона находится в QIII.

2. Выполните операцию, указанную для этого квадранта.

   Вычтите 180 из 240. Вы обнаружите, что 240–180 = 60, поэтому опорный угол составляет 60 градусов.

Об авторе книги

Мэри Джейн Стерлинг является автором Алгебра I для чайников и многих других книг для чайников .Она преподавала математику в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет и любила работать с будущими руководителями бизнеса, физиотерапевтами, учителями и многими другими.

.

Измерение и определение углов — манекены

2. Образование
3. Математика
4. Геометрия
5. Измерение и определение углов

Марк Райан

На карте вы прослеживаете свой маршрут и попадаете на развилку дорог. Две расходящиеся дороги расходятся от общей точки и образуют угол . . Точка, в которой дороги расходятся, — это вершина , вершина . Угол разделяет область вокруг него, известную в геометрии как плоскость , на две области.Точки внутри угла лежат во внутренней области угла, а точки вне угла лежат во внешней области угла.

Как только вы познакомитесь с типами углов и научитесь измерять и создавать свои собственные, вы приобретете ценные навыки геометрии, которые помогут вам решать даже самые сложные геометрические головоломки.

Для выполнения обеих задач вы используете транспортир, очень полезный инструмент (см. Рисунок 1).

Рисунок 1: Удобный транспортир.

Выбирая транспортир, постарайтесь найти из прозрачного пластика. Определить величину угла проще, потому что вы можете увидеть линию угла через транспортир.

Породы уголков

Существует несколько различных пород или типов уголков. Вы можете определить, какой у вас угол, по его мерке. Чаще всего угол измеряется в градусах . Вот краткое введение в четыре типа углов:

• Угол прямой. С этим углом вы никогда не ошибетесь. Прямой угол — один из самых легко узнаваемых. Он имеет форму буквы L и образует квадратный угол (см. Рисунок 2). Он имеет размер 90 градусов.

Рисунок 2: Прямой угол.

• Прямой угол. Знаете что? На самом деле это прямая линия. Большинство людей даже не думают об этом как об угле, но это так. Прямой угол состоит из противоположных лучей или отрезков прямой, имеющих общую конечную точку (см. Рисунок 3).Этот угол составляет 180 градусов.

Прямой и прямой углы довольно легко обнаружить, просто взглянув на них, но никогда не делайте поспешных выводов о величине угла. Лучше быть осторожным. Если информация не указана на странице, ничего не предполагайте. Измерьте.

Рисунок 3: Прямой угол.

• Острый угол. Это очаровательный угол .

Вообще-то, это всего лишь щепотка. Это любой угол, который составляет больше 0 градусов, но меньше 90 градусов.Острый угол находится где-то между несуществующим и прямым углом (см. Рисунок 4).

Рисунок 4: Острые углы — 45 ° (Рисунок a), 60 ° (Рисунок b) и 30 ° (Рисунок c).

• Тупой угол. Этот тип не так интересен, как острый угол. Его величина находится где-то между прямым и прямым углом (см. Рисунок 5). Это холм, на который нужно взобраться, гора, на которую нужно взобраться. Его размер больше 90 градусов, но меньше 180 градусов.

Рисунок 5: Тупые углы — 95 ° (Рисунок a), 125 ° (Рисунок b) и 175 ° (Рисунок c).

Измерение

Углы чаще всего измеряются в градусах, но для тех из вас, кто является приверженцем точности, можно использовать даже меньшие единицы измерения: минуты и секунды. Эти минуты и секунды похожи на те, что на часах: минута больше секунды. Представьте себе степень как час, и вы поняли: одна степень равна 60 минутам.Одна минута равна 60 секундам.

Прежде чем измерять угол, определите его и оцените, к какому типу он относится. Это прямой угол? Прямой угол? Острый или тупой? После того, как вы его оцените, измерьте угол. Выполните следующие действия:

1. Поместите выемку или центральную точку транспортира в точку, где встречаются стороны угла (вершина).

2. Поместите транспортир так, чтобы одна из линий угла, который вы хотите измерить, была равна нулю (фактически 0 °).

В использовании нулевой линии нет необходимости, потому что вы можете измерить угол, получив разницу в градусах одной линии с другой. Однако легче измерить угол, когда одна его сторона находится на нулевой линии. Наличие одной линии на нулевой линии позволяет вам считывать измерения непосредственно с транспортира без дополнительных математических расчетов. (Но если вы готовы принять вызов, выбейте себя из строя. )

3. Считайте число на транспортире в том месте, где вторая сторона угла пересекает транспортир.

Еще совет:

• Убедитесь, что ваша мера близка к вашей оценке. Это покажет вам, правильно ли вы выбрали масштаб. Если вы ожидали измерения острого угла, но получили очень тупую меру, вам нужно переосмыслить шкалу, которую вы использовали. Попробуйте другой.
• Если стороны вашего угла не достигают масштаба транспортира, вытяните их так, чтобы они достигли масштаба. Это повысит точность вашего измерения.
• Помните, что величина угла всегда является положительным числом.

Итак, что делать, если ваш угол не совсем соответствует масштабу транспортира? Взгляните на рисунок 6 для примера. Угол на этом рисунке имеет размер более 180 °. Что теперь? Извините, но в этом случае вам придется потратить немного больше энергии. Да, вам нужно заняться математикой. Эти углы известны как углы отражения, и их размер превышает 180 °.

Рис. 6: Углы отражения не помещаются на шкале транспортира, поэтому вам придется выполнить некоторые вычисления, чтобы их измерить.

Проведите линию так, чтобы получилась прямая линия (см. Расширенные точки на рисунке 6). Эта часть угла составляет 180 °, потому что это прямой угол. Теперь измерьте угол, образованный только что созданной выносной линией, и второй стороной исходного угла, который вы хотите измерить. (Если вы запутались, просто посмотрите на рисунок 6.) После того, как вы измерили второй угол, прибавьте это число к 180. Результатом будет общее количество градусов угла. На рисунке 6 180 ° + 45 ° = 225 °.

.

---

Смотрите также

• Как сделать слив с крыши в частном доме своими руками
• Как перекрыть крышу сарая рубероидом
• Как сделать подшивку крыши софитом
• Как утеплить крышу деревянного дома изнутри
• Как бороться с короедом на крыше
• Как сделать четырехскатную крышу для беседки
• Как бороться с конденсатом на крыше
• Как правильно сделать крышу на бане односкатную
• Как поменять крышу на гараже
• Как установить водосток на шиферную крышу
• Как сделать 4х скатную крышу для беседки

Угол наклона и наклон линии

Пусть прямая l пересекает ось x в точке A. Угол между положительной осью x и линией l, измеренный в направлении против часовой стрелки, называется углом наклона прямая л.

На приведенном выше рисунке, если θ – это угол прямой линии l, то мы имеем следующие важные моменты.

(i) 0° ≤ θ ≤ 180°

(ii)  Для горизонтальных линий θ = 0° или 180° и для вертикальных линий θ = 90°

(iii)  Если прямая линия изначально лежит вдоль оси х и начинает вращаться вокруг неподвижной точки А на оси х против часовой стрелки и, наконец, совпадает с осью х, то угол наклона прямой линии в начальном положении равно 0°, а линии в конечном положении равно 0°.

(iv)  Линии, перпендикулярные оси x, называются вертикальными линиями.

(v)  Линии, перпендикулярные оси Y, называются горизонтальными линиями.

(vi)  Другие линии, которые не перпендикулярны ни оси x, ни оси y, называются наклонными линиями.

Угол наклона и наклон линии – приложение

Основное применение угла наклона прямой линии – определение уклона.

Если θ – угол наклона прямой линии l, то tanθ называется наклоном градиента линии и обозначается буквой «m».

Следовательно, наклон прямой равен

м  = tan θ 

для 0° ≤ θ ≤ 180°

Найдем наклон прямой по приведенной выше формуле

(i)  Для горизонтальных линий угол наклона равен 0° или 180°.

То есть

θ = 0° или 180°

Следовательно, наклон прямой линии равен

м  = tan0° или tan 180°  = 0

(ii) Для вертикальных линий угол наклона равен 90°.

То есть

θ = 90°

Следовательно, наклон прямой равен

м  =  tan90°  =  Не определено

(iii) Для наклонных линий, если θ имеет острую форму, наклон положительный. Если же θ тупой, то наклон отрицательный.

Наклон линии — положительный или отрицательный, нулевой или неопределенный

Когда мы смотрим на прямую линию визуально, мы можем легко определить знак наклона.

Чтобы узнать знак наклона прямой, всегда нужно смотреть на прямую слева направо.

Это иллюстрируют приведенные ниже рисунки.

Решенные задачи

Задача 1 :

Найдите угол наклона прямой, наклон которой равен 1/√3.

Решение :

Пусть θ — угол наклона линии.

Тогда наклон линии составляет

M = TANθ

Дано: наклон = 1/√3

Затем,

1/√3 = tanθ

θ = 30 °

Итак, угол угла наклон 30°.

Задача 2 :

Если угол наклона прямой равен 45°, найдите ее наклон.

Решение :

Пусть θ — угол наклона линии.

Тогда, наклон линии,

M = TANθ

Дано: θ = 45 °

Затем,

M = TAN 45 °

M = 1

Итак, склон — 1.

40002 M = 1

Итак, склон — 1.

4

Задача 3 :

Если угол наклона прямой равен 30°, найдите ее наклон.

Решение :

Пусть θ — угол наклона линии.

Затем, наклон линии,

м = tanθ

Дано: θ = 30°

Тогда

м = tan30°

м = 1/√3

Итак, уклон равен √3

.

Задача 4 :

Найдите угол наклона прямой, наклон которой равен √3.

Решение :

Пусть θ — угол наклона линии.

Затем, наклон линии,  

м  = tanθ

Дано: Уклон  =  √3

Тогда, 

√3  =  tanθ  

θ  = 60°

Итак, угол наклона равен 60°.

Задача 5 :

Найдите угол наклона прямой, уравнение которой y = x + 32.

Решение :

Пусть θ — угол наклона линии.

Данное уравнение находится в форме пересечения наклона.

То есть

y = mx + b

Сравнивая

y = x + 32

и

y = mx + b,

получаем наклон 1. m = 9.0004

Мы знаем, что наклон линии равен

м  =  tanθ

Тогда

1  =  tanθ

θ  = 45°

Итак, угол наклона равен 45°.

Пожалуйста, отправьте свой отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

Угол наклона в задачах по физике

Автор: Эксперты по чайникам и

Обновлено: 26-03-2016

Из книги: Физика I: 501 практических задач для чайников (+ бесплатная онлайн-практика)

Физика I: 501 практических задач для чайников (+ бесплатная онлайн-практика)

Исследуйте книгу Купить на Amazon

По физике, если объект толкают вниз по склону, угол наклона склона влияет на ускорение объекта. Например, когда вы толкаете сани с покрытого льдом холма, вы можете рассчитать угол наклона холма, зная массу и ускорение саней.

Вес — гравитационная сила, с которой Земля воздействует на объект. У поверхности Земли вес равен массе, умноженной на 9,8 метра в секунду в квадрате. Величина силы трения равна коэффициенту трения, умноженному на величину нормальной силы. Трение всегда препятствует относительному движению двух поверхностей.

Вот несколько практических вопросов, которые помогут проиллюстрировать эту концепцию.

Практические вопросы

1. 25-килограммовые санки скользят по склону, покрытому ледяным снегом. Если сани движутся вниз по склону со скоростью 4,8 метра в секунду в квадрате, каков угол наклона холма по отношению к горизонтали?

   Предположим, что снег представляет собой поверхность без трения, и округлите ответ до ближайшего целого градуса.

2. Саманта толкает свою дочь, сидящую на санках, вниз по заснеженной горке с постоянным уклоном с силой 50 ньютонов. Сани разгоняются до 1,9метров в секунду в квадрате. Если общая масса ее дочери и санок равна 40 кг, каков угол наклона горки?

   Округлите ответ до ближайшего градуса.

Ответы

Ниже приведены ответы на практические вопросы:

1. 29 градусов.

   Сначала нарисуйте диаграмму свободного тела:

   Только одна сила направлена ​​вдоль оси движения

   , так что это единственный вклад в чистое ускорение вдоль поверхности холма:

2. 4 степени.

   Three forces are involved ( F _N , the normal force; F _G , the force due to Earth’s gravity; and F _P , сила толчка Саманты). Нарисуйте диаграмму свободного тела, показывающую векторы и любые необходимые компоненты, чтобы выровнять силы по двум перпендикулярным осям:

   Сани движутся вдоль оси, параллельной поверхности холма, так что это направление ускорения вам нужно изучить.