Как посчитать объем зная площадь: Как найти объем через площадь 🚩 как найти высоту куба 🚩 Математика

Как найти объем через площадь

Объем – мера вместимости, выраженная для геометрических фигур в виде формулы V=l*b*h. Где l – длина, b – ширина, h – высота объекта. При наличии только одной либо 2-х колляций вычислить объем в большинстве случаев невозможно. Впрочем при некоторых условиях представляется допустимым сделать это через площадь .

Инструкция

1. Задача первая: вычислить объем, зная высоту и площадь . Это самая простая задача, т.к. площадь (S) – это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема взамен l*b площадь . Вы получите выражение V=S*h.Пример: Площадь одной из сторон параллелепипеда – 36 см?, высота – 10 см. Обнаружьте объем параллелепипеда.V = 36 см? * 10 см = 360 см?.Результат: Объем параллелепипеда равен 360 см?.

2. Задача вторая: вычислить объем, зная только площадь

. Это допустимо, если вы вычисляете объем куба, зная площадь одной из его граней. Т.к. ребра куба равны, то извлекая из значения площади квадратный корень, вы получите длину одного ребра. Эта длина будет и высотой, и шириной.Пример: площадь одной грани куба – 36 см?. Вычислите объем.Извлеките квадратный корень из 36 см?. Вы получили длину – 6 см. Для куба формула будет иметь вид: V = a?, где а – ребро куба. Либо V = S*a, где S – площадь одной стороны, а – ребро (высота) куба.V = 36 см? * 6 см = 216 см?. Либо V = 6?см = 216 см?.Результат: Объем куба равен 216 см?.

3. Задача третья: вычислить объем, если вестима площадь и некоторые другие данные. Данные могут быть различные, помимо площади могут быть знамениты другие параметры. Длина либо ширина могут быть равны высоте, огромнее либо поменьше высоты в несколько раз. Также могут даваться добавочные данные о фигурах, которые помогут в вычислениях объема.Пример 1: обнаружьте объем призмы, если знаменито, что

площадь одной стороны 60 см?, длина 10 см, а высота равна ширине.S = l * b; l = S : bl = 60 см? : 10 см = 6 см – ширина призмы. Т.к. ширина равна высоте, вычислите объем:V=l*b*hV = 10 см * 6 см *6 см = 360 см?Результат:объем призмы 360 см?

4. Пример 2: обнаружьте объем фигуры, если площадь 28 см?, длина фигуры 7 см. Дополнительное условие: четыре стороны равны между собой, и объединены друг с ином по ширине.Для решения следует возвести параллелепипед. l = S : bl = 28 см? : 7 см = 4 см – ширинаКаждая сторона представляет собой прямоугольник, длина которого 7 см, а ширина 4 см. Если четыре таких прямоугольника объединить между собой по ширине, то получится параллелепипед. Длина и ширина в нем по 7 см, а высота 4 см. V = 7 см * 7 см * 4 см = 196 см?Результат: Объем параллелепипеда = 196 см?.

Строительный объем здания: что это такое, как считается общий строительный объем

Например, длина двух параллельных зданий — 30 м, их ширина — 15 м. Размеры перехода — 2,5 на 6 м. Значит, сначала нужно найти площадь одинаковых зданий: умножаем 15 на 30, получаем 450 м². Площадь перехода — 15 м². Складываем три площади: 450 + 450 + 15, получается 915 м². Если высота здания составляет 3 м, то строительный объем будет 2745 м³.

Здания с чердачными перекрытиями

Если в здании есть чердачное перекрытие, то строительный объем надземной части считают по особой формуле:

X = S¹ × h.

В этом случае под S¹ понимают площадь горизонтального сечения здания. Ее измеряют на уровне первого этажа выше цоколя, по внешнему обводу здания. Чтобы найти площадь, нужно также умножить ширину на длину здания, как и в расчетах по другим формулам.

Высоту h измеряют от верха чистого пола на первом этаже до верха засыпки чердачного перекрытия.

Допустим, площадь горизонтального сечения здания на уровне первого этажа составляет 420 м². Высота составляет 25 м. В этом случае строительный объем будет равен 10500 м³.

Если у здания есть поздемная часть, ее объем считают так же, как и в предыдущих случаях, а затем оба значения складывают.

Дома без чердачного перекрытия

Строительный объем надземной части зданий без чердачных перекрытий считают по другой формуле:

X = S² × L

S² — тоже площадь поперечного сечения, но не горизонтального, а вертикального. Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.

L — это длина здания, перпендикулярная прямая относительно вертикального поперечного сечения. Ее измеряют от одного торца здания к другому, тоже с учетом штукатурки и облицовки, на уровне первого этажа либо цоколя.

Например, нужно рассчитать объем здания высотой 6 м, длиной 23 м и шириной 4 м. Площадь вертикального поперечного сечения в этом случае составит 24 м², а строительный объем — 552 м³.

Если у здания есть подземная часть, ее также считают отдельно, а потом полученные значения суммируют.

Если известна общая площадь

Детальные данные, например, длину, высоту до определенных перекрытий и другие, не всегда указывают в технической документации. Поэтому строительный объем можно посчитать по другим формулам.

Если известна общая площадь, можно использовать формулу:

X = S × H × К

В этом случае S — сумма площадей всех этажей, или общая площадь. Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.

H в формуле — высота здания изнутри без учета перекрытий, так называемая высота в свету.

К — поправочный коэффициент, который учитывает толщину стен. Для жилых зданий он составляет 0,8.

То есть для расчета нужно знать всего два точных значения: общую площадь и высоту в свету. Допустим, площадь составляет 2 000 м², а высота в свету — 15 м. В этом случае показатель составит 24000 м³ с учетом поправочного коэффициента.

Если известна площадь застройки

Если известна площадь застройки, можно использовать другую формулу. В ней больше переменных, и выглядит она так:

X = S¹ × H¹ + S² × H²

S¹ в этом случае — площадь общей застройки. Ее можно найти, представив здание в виде геометрической фигуры или нескольких таких фигур, если постройка сложной формы. H¹ — высота дома, в которой можно не учитывать выступающие части крыши.

S² и H² — площадь и высота подвала соответственно. Площадь замеряют по внутренней обводке стен. Высоту — от верхней точки пола подвала до пола первого этажа.

Дома с мансардами

Мансарда — этаж в чердачном пространстве, фасад которого частично либо полностью образован поверхностями наклонной крыши. Обязательное условие — линия пересечения плоскости крыши и фасада должна находиться не больше, чем на высоте 1,5 м от уровня пола в мансарде. Согласно нормативам, строительный объем мансарды считается отдельно.

Чтобы найти строительный объем мансарды, нужно умножить площадь ее поперечного вертикального сечения на длину дома.

Ширину и высоту нужно измерять по внешнему обводу, вертикаль — до начала перекрытий. Все эти данные понадобятся для того, чтобы найти площадь вертикального сечения. Она равна половине произведения ширины, то есть основания, на высоту. Например, высота мансарды — 1,5 м, ширина, то есть основание — 6 м. Тогда площадь составит 9 м².

Полученное значение нужно умножить на длину дома. Например, она составляет 12 м. В этом случае строительный объем мансарды составит 108 м².

Оставшуюся надземную часть нужно считать по предыдущим формулам, но высоту измерять до начала основания мансарды, то есть до верхнего перекрытия. Объемы мансарды, надземной и подземной частей нужно просто сложить.

Если здание имеет сложную форму

Расчет строительного объема для зданий сложной формы — например, с мезонинами, башенками и различными пристроями — намного сложнее. В этом случае нужно сначала найти строительный объем каждого конструктивного элемента, а потом сложить полученные значения.

Полная формула расчета строительного объема зависит от исходных данных — есть ли подвал, предусмотрены ли чердачные перекрытия, построена ли мансарда. Чтобы получить точное значение, нужно провести тщательные замеры и использовать сложные схемы подсчета. Если не хотите тратить время на это, обратитесь к профессионалам — они посчитают все быстрее и точнее.

Как посчитать кубатуру помещения зная площадь. Как посчитать объем помещения

Для многих, кто сталкивается с пиломатериалом, вопрос о том, как посчитать кубатуру необрезной и обрезной доски остаётся сложным заданием. В принципе, это довольно легко и просто. Ниже мы рассмотрим основные способы расчёта кубатуры доски.

На уроках геометрии довольно часто приходилось рассчитывать объём чего – либо. Ситуация точно также обстоит с обрезными пиломатериалами. Просто нужно перемножить ширину на высоту и на длину. Естественно, не нужно это делать на целой пачке бруса или доски. Достаточно будет, если вы посчитаете кубатуру одной доски (бруса), затем просто нужно пересчитать общее количество досок в пачке и кубатуру одной доски помножить на посчитанное количество досок. Ещё одно важно правило, при расчёте кубатуры одной доски, все размеры нужно привести к единому измерению, то есть или всё переводится в сантиметры, миллиметры или же в метры. А замеры мы проводим по следующим параметрам: толщина, ширина, длина.

При расчёте кубатуры необрезной доски, тоже измеряется ширина, длина и высота. Только в необрезных пиломатериалах невозможно рассчитать кубатуру одной доски, поэтому доску нужно уложить в пачку, обмерять и применить различные коэффициенты. Для более точного расчёта, лучше всего сложить доску в одну стопку, затем измерить посередине самую широкую и самую тонкую доски, далее сложить эти два показателя и разделить на два. В результате мы получим усреднённую ширину. А длину и высоту измеряем как обычно.

Далее нужно помножить толщину стопки на ширину и длину и применить понижающий коэффициент. По ГОСТу, для полубруса он составляет 0,5, а для необрезной доски 0,63. Но, очень часто, для упрощения расчётов, производители на пилорамах производят отгрузку пиломатериала, которые имеют коэффициент 0,7. Когда таким образом будет посчитана одна стопка, нужно переходить ко второй, третьей и так, до тех пор, пока не будет пересчитан весь пиломатериал.

Как посчитать кубатуру фундамента

• столбчатый
• ленточный
• плитный

При расчёте кубатуры фундамента столбчатого типа, сначала нужно рассчитать кубатуру одного бетонного столбика. Для этого умножается длина на ширину. Если же применяются столбики круглого сечения, то умножается радиус квадрата на коэффициент «Пи – 3,14» и получившийся результат умножаем на высоту столбика. Далее результат перемножается на общее количество столбиков, которые размещены по территории. Это и будет общая кубатура фундамента. В тех случаях, когда столбики соединены раствором, то нужно воспользоваться формулой параллелепипеда.

При расчёте кубатуры фундамента ленточного типа сначала определяется вид сечения. Когда оно одинаковое, то периметр территории умножается на толщину и длину. В том случае, когда оно разное, необходимо просто рассчитать объёмы каждого участка по отдельности и в итоге, сложить все полученные результаты.

Объём — количественная характеристика пространства. Объём помещения определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. Принятые единицы измерения — в ситме измерений СИ и производных от неё — кубический метр м3, кубический сантиметр, литр.

Вам понадобится

• Для измерения объема помещения вам потребуется рулетка, лист бумаги, калькулятор, ручка.

Инструкция

Каждое помещение, например комната, представляет собой, с геометрической точки зрения прямоугольный параллелепипед. Параллелепипед — это объемная фигура, у которой шесть граней (например комната: 4 стены, потолок, пол), и каждая из них является прямоугольником. Формула нахождения объёма прямоугольного параллелепипеда: V=abc. Объем прямоугольного параллелепипеда равен произведению трех его измерений. Кроме этой формулы можно измерить объем помещения умножив площадь пола на высоту.

Итак приступайте к вычислениям объема помещения. Измерьте длину одной стены (длинной стены),потом измерьте длину второй стены (короткой стены). Измерения проводите по полу, на уровне плинтуса.Ленту рулетки держите ровно. Теперь измерьте высоту помещения, для этого подойдите к одному из его углов, и точно померьте высоту по углу от пола до потолка. Полученные данные запишите на листочек, чтобы не забыть. Теперь приступайте к вычислениям: умножите длину длинной стены на длину короткой стены, полученное произведение (число)умножите на высоту и вы получите требуемый результат. помещений вычисляют в различных случаях: 1) в случае покупки кондиционера воздуха, так как кондиционеры рассчитаны на определенный объем помещений- 2) с случае установки радиаторов отопления в комнатах, так как количество секций в радиаторе напрямую зависит от объема помещения.

Если у вас комната неправильной формы, то есть состоит из как бы большого параллелепипеда и маленького. В данном случае необходимо измерить объем каждого из них отдельно, а потом сложить. Если в вашей комнате есть альков (ниша полукруглой формы), тогда его объем нужно высчитывать по формуле объема . Объем всякого цилиндра равен произведению площади основания на высоту: V=? r2 h, где? – это число «пи» равное 3,14, r2 квадрат радиуса цилиндра, h – высота. Представьте себе ваш альков как часть цилиндра, вычислите объем как бы всего цилиндра, потом посмотрите какую часть этого цилиндра занимает ваш альков,отнимите от общего объема лишнюю часть.

Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.

Инструкция

Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения . Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели и вы получите искомый объем.

Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения . Измерения необходимо проводить в одних и тех же единицах, например, в метрах.

При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.

При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.

Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания.

Полезный совет

При измерения радиуса алькова, пользуйтесь ниткой с иголкой, иголку воткните в воображаемый центр цилиндра и тяните нитку до стены, потом измерьте её длину.

Как найти объем помещения. Как рассчитать, посчитать объем помещения

 

Как рассчитать, посчитать объем помещения.

Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.

1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.

2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.

3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.

4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.

5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.

Формула объема помещения

Формула

 

Пример расчета объема помещения по формуле

Калькулятор площади стены или пола

Вставьте размеры помещения и получите результат.

Как посчитать объем цилиндра — онлайн калькулятор

Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

• радиус r и высоту h цилиндра
• диаметр d и высоту h цилиндра
• площадь основания S_o и высоту h цилиндра
• площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

V = π⋅r²⋅h

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2² ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см³

Зная диаметр d и высоту h

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

V = π⋅(^d/₂)²⋅h

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ (¹/₂)² ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см³

Зная площадь основания S_o и высоту h

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

V = S_o⋅h

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см², то:

V = 10 ⋅ 5 = 50 см³

Зная площадь боковой поверхности S_b и высоту h

Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?

Формула

V = ^S_b2/_4πh

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см², то:

V = ³⁰²/ _{4 ⋅ 3.14⋅ 5} = ⁹⁰⁰/_62.8 = 14.33 см³

См. также

Расчетный объем | SkillsYouNeed

На этой странице объясняется, как рассчитать объем твердых объектов, то есть насколько вы можете поместиться в объекте, если, например, вы заполните его жидкостью.

Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).

Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.

В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.

Однако это все еще может быть важным. Возможность рассчитать объем позволит вам, например, определить, сколько у вас есть места для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете уместить в банку.

Это также может быть полезно для понимания того, что средства массовой информации имеют в виду, когда говорят о пропускной способности плотины или течении реки.

---

Примечание к агрегатам

---

Площадь выражается в квадратных единицах, потому что это два измерения, умноженные вместе.

Объем выражается в кубических единицах, потому что это сумма трех измерений (длина, ширина и глубина), умноженных вместе. Кубические единицы включают см ³ , м ³ и кубические футы.

ВНИМАНИЕ!

Объем также можно выразить как вместимость по жидкости.

Метрическая система

В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, поскольку 1 мл = 1 см ³ .1 литр = 1000 мл = 1000 см ³ .

Британская / английская система

В британской / английской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше всего придерживаться жидких или твердых единиц объема.

Подробнее см. На нашей странице Системы измерения

---

Основные формулы для расчета объема

Объем твердых тел на основе прямоугольников

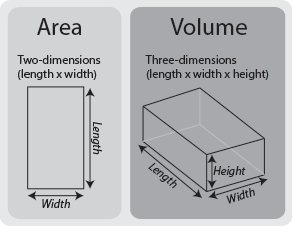
В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.

То, как вы относитесь к разным размерам, не меняет расчет: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что все три измерения умножаются. Вы можете умножать в любом порядке, поскольку это не изменит ответ (подробнее см. Нашу страницу о умножении ).

Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см ³

---

Объем призм и цилиндров

Эта базовая формула может быть расширена для охвата цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.

Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.

Таким образом, основная формула для определения объема призм и цилиндров:

Площадь формы торца × высота / глубина призмы / цилиндра.

---

Объем конусов и пирамид

Тот же принцип, что и выше (ширина × длина × высота), применяется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем — это только пропорция от общего количества, которое было бы, если бы они продолжались. в той же форме насквозь.

Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.

Следовательно, формула:

Площадь основания или торца × высота конуса / пирамиды × ¹ / ₃

Вернитесь на нашу страницу Расчет площади , если вы не можете вспомнить, как рассчитать площадь круга или треугольника.

Например, чтобы рассчитать объем конуса с радиусом 5 см и высотой 10 см:

Площадь внутри круга = πr2 (где π (пи) приблизительно равно 3.14 и r — радиус круга).

В этом примере площадь основания (круга) = πr ² = 3,14 × 5 × 5 = 78,5 см ² .

78,5 × 10 = 785

785 × 1/3 = 261,6667 см ³

---

Объем сферы

Как и в случае с кругом, вам нужно π (пи), чтобы вычислить объем сферы.

Формула: 4/3 × π × радиус ³ .

Вам может быть интересно, как вычислить радиус шара.Если не протыкать через него спицу (эффективный, но конечный для мяча!), Есть более простой способ.

Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.

Длина окружности вычисляется как радиус 2 x π x.

Чтобы вычислить радиус из окружности, вы:

Разделите окружность на (2 x π) .

---

Рабочие примеры: расчет объема

Пример 1

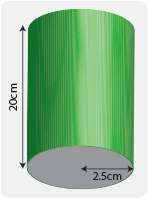
Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.

Сначала обработайте площадь одного из круглых концов цилиндра.

Площадь круга равна πr ² (π × радиус × радиус). π (пи) приблизительно равно 3,14.

Таким образом, площадь конца равна:

3.14 x 2,5 x 2,5 = 19,63 см ²

Объем — это площадь конца, умноженная на длину, и, следовательно, составляет:

19,63 см ² x 20 см = 392,70 см ³

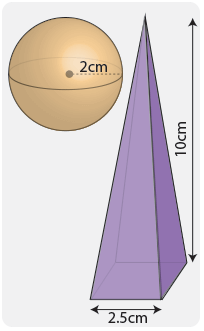
Пример 2

Что больше по объему: сфера радиусом 2 см или пирамида с основанием в квадрате 2,5 см и высотой 10 см?

Сначала определим объем сферы .

Объем сферы составляет 4/3 × π × радиус ³ .

Таким образом, объем сферы:

4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см ³

Затем вычислите объем пирамиды .

Объем пирамиды 1/3 × площадь основания × высота.

Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см ²

Объем, следовательно, равен 1/3 x 6,25 × 10 = 20.83см ³

Таким образом, сфера больше по объему, чем пирамида.

---

Расчет объема твердых тел неправильной формы

Так же, как вы можете вычислить площадь неправильных двухмерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите только твердые тела, с которыми вы сможете легко работать.

Рабочий пример

Рассчитайте объем водяного цилиндра общей высотой 1 м, диаметром 40 см и полусферической верхней частью.

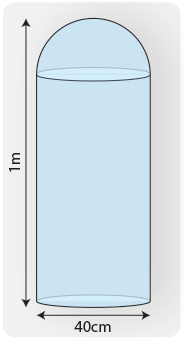
Сначала вы делите фигуру на две части: цилиндр и полусферу (полусферу).

Объем сферы составляет 4/3 × π × радиус ³ . В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть полусферической формы, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:

.

0,5 × 4/3 × π × 203 = 16,755,16 см ³

Объем цилиндра равен площади основания × высоте.Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь базы ² грн.

Таким образом, объем цилиндрического сечения данной формы составляет:

80 × π × 20 × 20 = 100 530,96 см ³

Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см ³ .

Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см ³ ). Однако вполне правильно выразить его как cm ³ , поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.

---

В заключение…

Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем практически всего в своей жизни, будь то упаковочный ящик, комната или водяной баллон.

,

Площадь куба с вычислителем

Площадь поверхности куба с калькулятором — Math Open Reference

Определение: Количество квадратных единиц, которые точно покрывают поверхность куба.

Попробуй это Перетащите ползунок, чтобы изменить размер куба. Площадь поверхности рассчитывается при перетаскивании. Также поверните куб, перетащив его.

Как найти площадь поверхности куба

Напомним, что все ребра куба имеют одинаковую длину (см. Определение куба).Это означает, что каждая из шести граней куба представляет собой квадрат. Таким образом, общая площадь поверхности в шесть раз больше площади одного лица.

Или как формула:

Где s — длина любого ребра куба.

Если вы знаете площадь поверхности

Если вы уже знаете площадь, вы можете найти длину края, изменив формулу выше: где a — площадь поверхности.

Квартир

Помните, что длина края и площадь поверхности будут в одинаковых единицах.Таким образом, если длина края указана в милях, то площадь поверхности будет в квадратных милях и так далее.

Калькулятор

Воспользуйтесь калькулятором выше, чтобы вычислить свойства куба.

Введите любое одно значение, и остальные будут рассчитаны. Например, введите длину стороны, и будет рассчитан объем.

Точно так же, если вы введете площадь поверхности, будет рассчитана длина стороны, необходимая для получения этой площади.

Что попробовать

• Установите флажок «разнести».Поверните куб, перетащив его, чтобы более четко увидеть, что куб имеет шесть одинаковых квадратных граней.
• На рисунке выше перетащите ползунок, чтобы изменить размер куба. Обратите внимание, как пересчитывается площадь поверхности.
• Нажмите «скрыть детали». Измените размер куба с помощью ползунка. Рассчитайте площадь поверхности, затем нажмите «Показать подробности», чтобы проверить свой ответ.

Связанные темы

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

,

Объем частично заполненного баллона с вычислителем

Объем частично заполненного цилиндра с калькулятором — Math Open Reference

Определение: форма, образующаяся при разрезании цилиндра плоскостью, параллельной его сторонам.

Попробуй это Перетащите оранжевые точки, обратите внимание на изменение громкости.

Если мы возьмем горизонтальный цилиндр и разрежем его на две части, используя надрез, параллельный сторонам цилиндра, мы получим два горизонтальных сегмента цилиндра.На рисунке выше нижний показан синим цветом. Другой — прозрачная часть сверху.

Если мы посмотрим на конец цилиндра, мы увидим, что это круг, разрезанный на два сегмента. Подробнее см. Определение сегмента круга.

Если у нас есть твердое тело, поперечное сечение которого одинаково по длине, мы всегда можем найти его объем, умножив площадь конца на его длину. Таким образом, в этом случае объем сегмента цилиндра равен площади сегмента круга, умноженной на длину.

Итак, формула объем горизонтального цилиндрического сегмента равен Где
s = площадь сегмента круга, образующего конец твердого тела, а
l = длина цилиндра.

Площадь сегмента круга может быть найдена по его высоте и радиусу круга.
См. Площадь сегмента круга с учетом высоты и радиуса.

Калькулятор

Воспользуйтесь калькулятором ниже, чтобы рассчитать объем горизонтального сегмента цилиндра.Он создан для практического случая, когда вы пытаетесь определить объем жидкости в цилиндрическом резервуаре. измеряя глубину жидкости.

Для удобства он преобразует объем в жидкие измерения, такие как галлоны и литры, если вы выберете нужные единицы. Если вы не укажете единицы измерения, объем будет в тех единицах, которые вы использовали для ввода размеров. Например, если вы использовали футов, тогда объем будет в кубических футах. Используйте одинаковые единицы для всех трех входов.

Как формула

объем = где:
R — радиус цилиндра.
D — это глубина.
L — длина цилиндра Примечания :

• Результат функции cos ^-1 в формуле выражен в радианах.
• В формуле используется радиус цилиндра. Это половина его диаметра.
• Все входы должны быть в одних и тех же единицах. Результат будет в этих кубических единицах. Так, например, если входные данные указаны в дюймах, результат будет в кубических дюймах. При необходимости результат должен быть преобразован в единицы объема жидкости, такие как галлоны.

Связанные темы

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

,