Как посчитать площадь двери в квадратных метрах? Калькулятор
domolov | 24.04.2014 | Помощь в ремонте | Комментариев нет
Для расчёта на нашем калькуляторе не нужно даже нажимать кнопки. Достаточно лишь вставить значения ширины и высоты и вы получите мгновенный результат — площадь двери. Удобно? Конечно же да! Хотим отметить, что расчёт ведётся только для прямоугольных дверей. Также стоит напомнить, что разделителем дробных значений служит точка.
Высоту и ширину окна вводите в сантиметрах (см)!
Калькулятор расчёта площади двери в кв. м.
Теория расчёта площади двери.
Для вычисления площади двери нам нужно умножить следующие параметры между собой — высоту и ширину двери. Если высота двери у на «Х», а ширина — «У», то наша площадь двери «S» равна Х*У.
S=Х*У
, где
Х — высота нашей двери,
У — ширина нашей двери.
Из-за того, что мы ширину и высоту двери померили в сантиметрах, то нам необходимо оба эти параметра заранее поделить на 100, чтобы перевести значения в сантиметрах в метры. В итоге формула площади двери будет следующая: S=Х/100*У/100.
Пример расчёта площади полотна двери.
Например, берём ширину нашей двери 222 см, а высоту полотна двери 82 см. Затем переводим параметры в метры — т.е. делим значения высоты и ширины на 100. Получаем: ширина нашей двери 2,22 м, а высота двери 0,82м. Теперь умножаем их друг на друга (наши значения в метрах), т.е. делаем вот так 0,82*2,22. Получаем ответ: 1,8204 м2 — это и есть площадь нашей двери.
Зачем высчитывать площадь двери.
Довольно часто во время косметического или капитального ремонта, да и просто в жизни, появляется необходимость вычисления площади каких-либо предметов или составляющих комнаты.
К примеру — нахождение площади вашего дверного проёма или самой двери.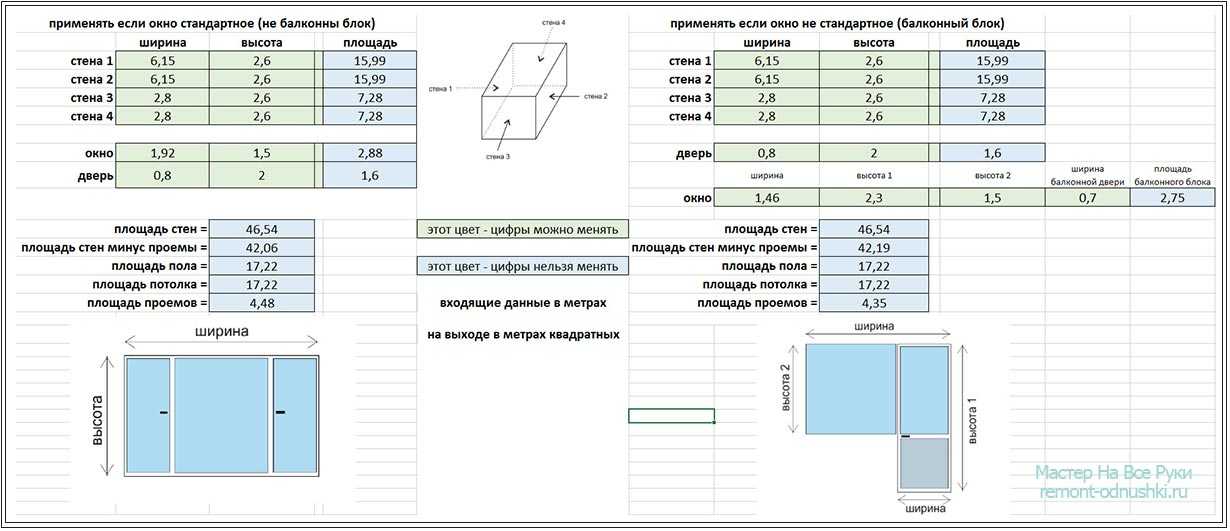
Это может быть необходимо не только для заказа новой межкомнатной или входной двери в квартиру, но и в случаях, когда эту площадь двери нужно отнять от площади стены.
Вот эти «отнимания» разрешат нам сделать наиболее правильный и корректный расчёт, например, точное вычисление площади стен. Таким образом, площадь стен вы будете считать с большой точностью, при этом и краску для стен и обои вы будете приобретать в нужном количестве.
Это не только позволит сэкономить ваши средства, но и сэкономит ваше время, лишив вас возможности делать ненужный возврат купленных с излишком материалов для ремонта.
Данный калькулятор допустимо применять для вычисления площадей различных прямоугольных форм: окон, шкафов, потолка, пола и т.п.
Другие калькуляторы:
Калькулятор расчёта площади стен
Калькулятор расчёта плитки на пол
Калькулятор расчёта площади окна
Квадратный метр: это сколько и как быстро рассчитать площадь комнаты в калькуляторе
Что такое квадратный метр и как правильно его рассчитать? Возможно, вы уже задавались этим вопросом, когда планировали ремонт или строительство своего дома.
С квадратным метром мы довольно часто сталкиваемся в повседневной жизни. И от правильных расчетов порой зависит и количество сэкономленных денег в кошельке. Именно поэтому нужно уметь рассчитать “квадраты” правильно и без ошибок.
Содержание
- Что такое квадратный метр
- Что такое площадь
- Сфера применения площади в квадратных метрах
- Что такое 1 см² и 1 м²
- Перевод квадратных сантиметров в квадратные метры
- Формула подсчета квадратных метров
- Инструменты для подсчета квадратных метров
- Что понимается под погонным метром
- Как квадратные метры перевести в погонные и просто в метры
- Пример 1
- Пример 2
- Как посчитать площадь квартиры в квадратных метрах
- Как посчитать квадратные метры стены с дверью
- Как посчитать квадратные метры стены с окном
- Как посчитать площадь комнаты в квадратных метрах
- Площадь пола или потолка
- Площадь сплошной стены
- Скошенные углы в комнате
- Помещения с нишами и выступами
- Вычисление площади квадратуры помещения неправильной формы
- Объем комнаты
- Пример расчета количества обоев
- Как посчитать площадь земельного участка
- Геометрические вычисления
- Простые фигуры
- Треугольники
- Площадь круга
- Калькулятор квадратных метров
- Преобразование квадратного метра в разные единицы измерения
- Видео Определить площадь стен комнаты
Что такое квадратный метр
Квадратный метр – единица измерения площади, которая равна площади квадрата со стороной, равной одному метру.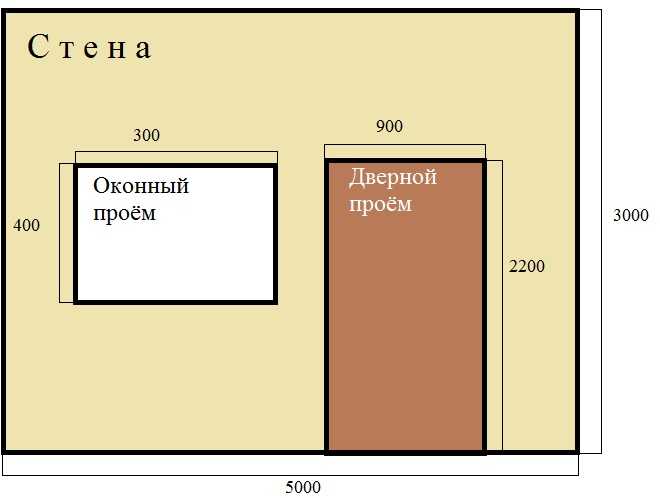
Иными словами, это площадь поверхности, которая занимает квадрат со стороной в один метр. Эта единица широко используется, чтобы измерять площадь земельных участков, помещений, стен, потолков и других поверхностей.
Что такое площадь
Площадь — это величина, которая показывает, сколько места занимает поверхность. Величина может быть вычислена для любой поверхности, включая стены, полы, потолки, квартиры, дома, земельные участки и т.д.
Сфера применения площади в квадратных метрах
В строительстве и архитектуре квадратный метр используется для определения площади помещений, фасадов зданий, участков земли и других объектов. В торговле и бизнесе “квадраты” используются для расчета площади помещений и складских площадей. В науке и инженерии они используются для измерения площади поверхности и объема объектов.
1 м2 = 1 м * 1 мТакже они широко применяются в сфере искусства и дизайна для расчета площади квартир, комнат и декоративных элементов. Например, для расчета площади стен и потолков, которые нужно покрасить или облицевать.
Что такое 1 см² и 1 м²
1 см² и 1 м² – стандартные единицы измерения площади:
- 1 см² представляет собой квадрат со стороной в 1 сантиметр,
- 1 м² – квадрат со стороной в 1 метр.
Несмотря на то, что эти две единицы измерения различаются на несколько порядков, они оба являются фундаментальными единицами измерения площади в системе СИ.
1 м² соответствует 10 000 см², что делает его более удобным для измерения площадей крупных объектов, таких как земельные участки и здания, тогда как 1 см² может быть полезен для измерения более мелких объектов.
Перевод квадратных сантиметров в квадратные метры
Для этого площадь делят на 10 000. Другими словами, 1 м² равен 10 000 см², и наоборот, 1 см² квадратный = 0,0001 м².
К примеру, если площадь квадрата составляет 2 500 квадратных сантиметров, то, разделив ее на 10 000, получаем 0,25 квадратных метра.
Формула подсчета квадратных метров
Формула зависит от формы фигуры:
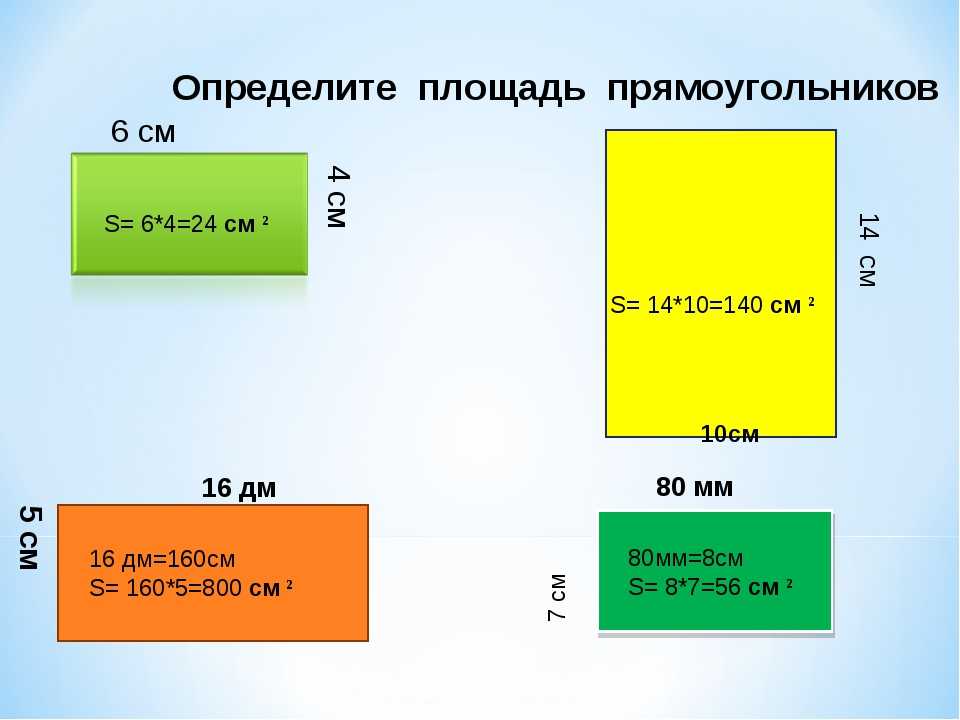
- Формула расчета площади прямоугольника: S = a × b, где a и b – длины сторон фигуры.
- Формула расчета площади круга: S = π × r², где π – математическая константа (приблизительно равна 3,14), r – радиус круга.
- Формула расчета объема цилиндра: V = π × r² × h, где π – математическая константа (приблизительно равна 3,14), r – радиус основания цилиндра, h – высота цилиндра.
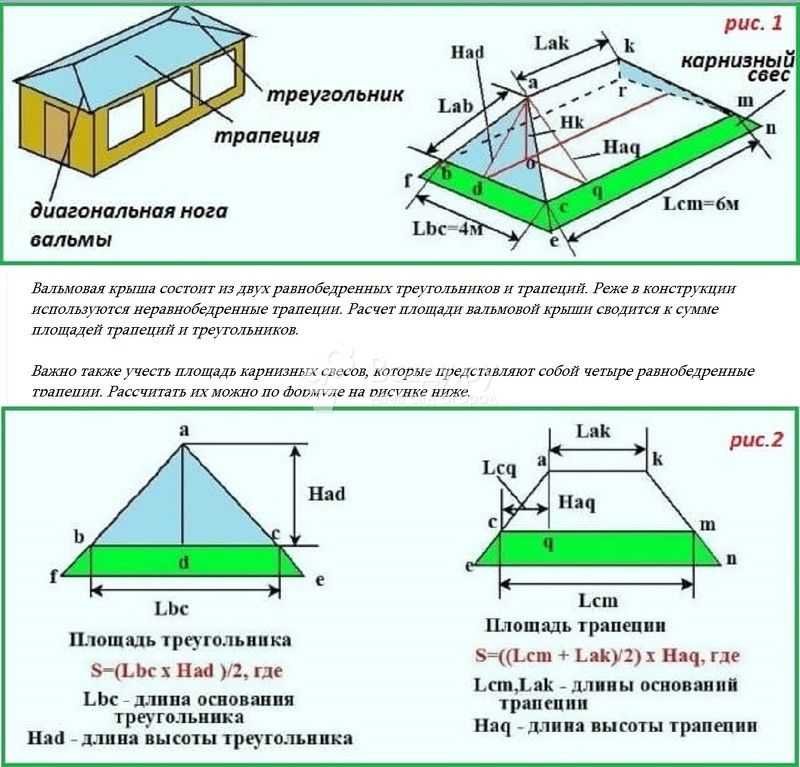
- Формула расчета площади треугольника: S = 0,5 × a × h, где a – длина основания треугольника, h – его высота.
- Формула расчета объема параллелепипеда: V = a × b × h, где a, b и h – длины трех сторон параллелепипеда.
- Формула расчета площади трапеции: S = 0,5 × (a + b) × h, где a и b – длины оснований трапеции, h – высота трапеции.
Инструменты для подсчета квадратных метров
Для подсчета квадратных метров нужны специальные инструменты, которые помогут измерить площадь поверхности. Вот несколько наиболее распространенных инструментов для подсчета квадратных метров:
- Линейка: это простой и доступный инструмент, которым измеряются длина и ширина поверхности.
- Рулетка или мерная лента: это еще один простой инструмент, который позволяет измерять расстояния. Рулетки бывают разных размеров и могут измерять длину как в метрах, так и в сантиметрах.
- Лазерный дальномер: это современный инструмент, который использует лазерные лучи для измерения расстояний и площадей. Он позволяет быстро и точно измерить площадь поверхности.
- Планиметр: это специальный инструмент, который работает на основе математических принципов. Он может пригодиться при работе с нестандартными поверхностями.
- Программы для измерения площади на смартфонах: это удобные и простые в использовании приложения, которые позволяют измерять площадь поверхности, используя камеру смартфона. Они могут быть очень полезны при работе с небольшими поверхностями. Однако, для точных замеров лучше всего использовать линейку и рулетку.
Выбор инструмента зависит от конкретной задачи и индивидуальных предпочтений. Однако важно помнить, что точность измерений напрямую зависит от правильного использования инструмента и правильности проведения измерений.
Что понимается под погонным метром
Погонный метр – это измерение длины, которое часто используется в строительстве и текстильной промышленности. Он обозначает длину одного метра ленты, тесьмы или материи с шириной в один метр, которая может быть использована в качестве отдельного элемента или полосы. Таким образом, погонный метр представляет собой линейную меру, которая выражается в метрах и определяет длину материала, используемого в конкретном проекте.
Для примера, если имеется рулон ткани шириной 1 метр и длиной 10 метров, то общая площадь этого рулона составляет 10 квадратных метров, а его длина будет равна 10 погонным метрам.
Погонный метр также может использоваться для определения длины различных элементов, таких как трубы, кабель или молдинги. В таких случаях погонный метр определяется как длина одного метра материала с заданной шириной, и измеряется в линейных метрах.
Важно отметить, что погонный метр может использоваться как для измерения длины материалов с произвольной шириной, так и для измерения длины материалов с фиксированной шириной в один метр.
Как квадратные метры перевести в погонные и просто в метры
Некоторые путают понятия “квадратный метр” и “погонный метр”. “Квадраты” используются для измерения площади, а погонные метры – для измерения длины.
1 м погонный отрезкаПример 1
Пусть у нас есть помещение размером 4 метра в длину и 3 метра в ширину. И для того чтобы найти его площадь, нужно умножить длину на ширину: 4 м x 3 м = 12 м². А чтобы перевести это значение в погонные метры, нужно умножить площадь на 4 (так как в одном погонном метре 4 квадратных метра): 12 м² x 4 = 48 погонных метров.
Если же нам нужно перевести это значение обратно в метры, мы должны разделить количество погонных метров на 4: 48 погонных метров / 4 = 12 метров.
Пример 2
Допустим, мы хотим выложить тротуар, площадью 20 м², плиткой размером 30 см х 30 см. Чтобы узнать количество плитки в квадратных метрах, нужно сначала посчитать площадь одной плитки:
0,3 м x 0,3 м = 0,09 м².
Затем мы можем разделить общую площадь тротуара на площадь одной плитки: 20 м² / 0,09 м² = 222,22.
Таким образом, нам нужно приобрести 222 целых плиток. Если мы хотим вычислить длину каждой стороны тротуара, то можем воспользоваться формулой площади: длина = площадь / ширина.
Как посчитать площадь квартиры в квадратных метрах
Для этого измерьте длину и ширину каждой комнаты в квартире, а затем перемножьте эти значения друг с другом.
К примеру, пусть длина комнаты равна 5 метрам, а ширина равна 4 метрам. Тогда площадь комнаты будет равна 20 квадратных метров (5 * 4 = 20).
Нужно повторять эти нехитрые подсчеты для каждой комнаты в квартире, а затем суммируйте результаты.
Как посчитать квадратные метры стены с дверью
Для этого нужно измерить ширину и высоту стены без учета двери, а затем отминусовать площадь дверного проема из общей площади.
Например, предположим, что ширина стены без двери составляет 3 метра, а высота – 2,5 метра. Дверной же проем имеет ширину 0,9 метра и высоту 2 метра.
Сначала необходимо найти площадь стены без двери, умножив ширину на высоту:
3 м × 2,5 м = 7,5 м²
Затем находим площадь дверного проема, умножив ширину на высоту:
0,9 м × 2 м = 1,8 м²
Наконец, вычитаем площадь дверного проема из общей площади стены:
7,5 м² – 1,8 м² = 5,7 м²
Таким образом, площадь стены с дверью составляет 5,7 квадратных метров.
Как посчитать квадратные метры стены с окном
Для этого необходимо измерить ширину и высоту стены, а также высоту и ширину окна.
Затем необходимо вычислить площадь всей стены, умножив ширину на высоту, и вычесть из этого значения площадь окна. Для этого нужно умножить ширину окна на его высоту и вычесть полученное значение из общей площади стены.
Формула для подсчета площади стены с окном будет выглядеть следующим образом:
S стены = (ширина стены x высота стены) – (ширина окна x высота окна)
Это и будет являться площадью такой стены.
Как посчитать площадь комнаты в квадратных метрах
Тут нет ничего сложного – измерьте длину и ширину комнаты с помощью измерительной ленты, затем перемножьте эти два значения. Это и есть площадь комнаты в “квадратах”.
Площадь пола или потолка
Этот параметр рассчитывается на основании длины и ширины помещения. Для расчета площади пола или потолка необходимо умножить длину на ширину.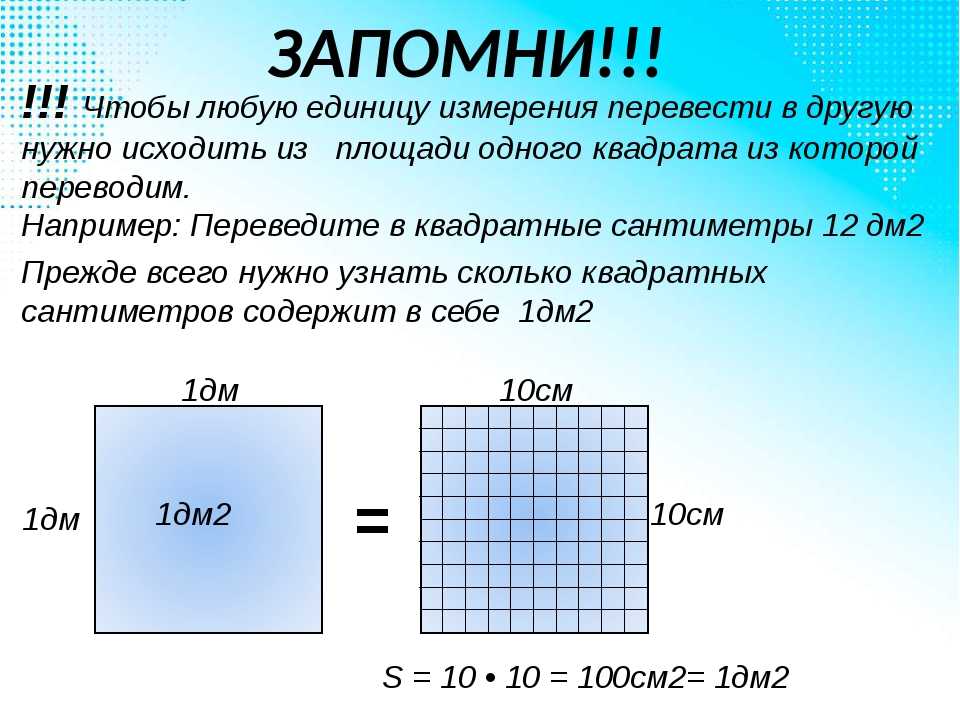
Площадь сплошной стены
Измерьте высоту и длину стены в метрах. А затем перемножьте эти значения. Не забывайте, что стены могут иметь неровности, выступы или выемки, которые могут усложнить измерение и расчет площади. Попробуйте использовать более точные инструменты, такие как лазерный дальномер, чтобы получить более точные измерения.
Скошенные углы в комнате
Безусловно, скошенные углы могут придать комнате необычный и оригинальный вид. Но как их учесть при расчете площади? В этой ситуации нужно прибегнуть к некоторым математическим формулам.
Для начала необходимо измерить длину каждой стены, включая скошенные углы. Затем может подойти формула для расчета площади треугольника:
S = (a * b) / 2, где a – длина одной стороны треугольника (скошенного угла), b – высота (расстояние от угла до противоположной стены).
После этого нужно сложить площади всех треугольников и полученную сумму добавить к общей площади комнаты.
Таким образом, скошенные углы не будут помехой при расчете площади комнаты.
Помещения с нишами и выступами
Помещения с нишами и выступами могут быть необычной формы и вызвать затруднения при подсчете площади. И чтобы верно рассчитать площадь, необходимо определить площади каждой части помещения отдельно, после чего – их сложить.
Для ниш и выступов можно применить следующую методику:
- Измерьте длину, ширину и высоту ниши/выступа.
- Рассчитайте площадь стенок, образующих нишу/выступ. Для этого умножьте длину на высоту каждой стенки и сложите полученные значения.
- Рассчитайте площадь ниши/выступа. Для этого умножьте длину на ширину.
- Добавьте площадь стенок и площадь ниши/выступа. Так вы получите общую площадь.
Вычисление площади квадратуры помещения неправильной формы
Для удобства, в этой ситуации нужно разделить на более простые геометрические фигуры, а затем сложить полученные значения.
- Если в помещении есть части, которые можно приблизительно описать как прямоугольники, измерьте их длину и ширину и умножьте эти значения друг на друга, чтобы вычислить их площадь. Например, если часть стены в форме прямоугольника имеет длину 4 метра и ширину 2 метра, то площадь этой части составляет 8 квадратных метров.
- Если в помещении есть части, которые можно приблизительно описать как треугольники, измерьте их высоту и основание, а затем используйте формулу для вычисления площади треугольника: S = 1/2 * a * h, где “а” – основание треугольника, а “h” – высота, опущенная на это основание. Например, если часть стены имеет высоту 3 метра и основание 2 метра, то ее площадь будет равна 3 * 2 * 0,5 = 3 квадратных метра.
Например, если часть стены в форме прямоугольника имеет длину 4 метра и ширину 2 метра, то площадь этой части составляет 8 квадратных метров.После этого сложите все полученные значения Не забывайте, что для точных результатов нужно использовать точные измерения. И чем больше измерений вы сделаете, тем более точный результат вы получите.
Объем комнаты
Объем комнаты – это количество трехмерного пространства, занимаемого комнатой. Для вычисления объема комнаты, необходимо измерить ее длину, ширину и высоту. После этого умножьте эти три значения вместе.
Например, если длина комнаты составляет 5 метров, ширина – 3 метра, а высота – 2.5 метра, то формула будет следующей:
V = l × w × h
V = 5 м × 3 м × 2,5 м = 37,5 м³
Таким образом, объем комнаты составляет 37,5 кубических метров.
Если же комната имеет сложную форму, то объем можно разделить на несколько более простых геометрических фигур, таких как прямоугольник или квадрат. После этого необходимо вычислить объем каждой фигуры и суммируйте результаты.
Пример расчета количества обоев
Для правильного выбора количества рулонов обоев нужно знать размеры комнаты, высоту потолков и ширину рулона обоев.
Пример расчета:
- Посчитайте площадь каждой стены.
- Сложите площади стен, чтобы узнать ее общее значение.
- Умножьте эту цифру на коэффициент запаса (обычно 1,1 или 1,2), чтобы учесть потери при резке и стыковке обоев.
- Разделите полученный результат на площадь рулона (обычно 5,3 квадратных метра).
Так вы получите цифру рулонов, необходимых для отделки стен комнаты.
Например, если площадь всех стен в комнате составляет 40 квадратных метров, и у вас выбраны обои с площадью 5,3 квадратных метров на рулон, то для отделки комнаты вам потребуется около 8 рулонов.
| Высота потолков 2,5 метров | Высота потолков 2,6 – 3 метра | ||
|---|---|---|---|
| Площадь помещения | Количество рулонов | Площадь помещения | Количество рулонов |
| 6 | 5 | 6 | 7 |
| 10 | 6 | 10 | 9 |
| 12 | 7 | 12 | 10 |
| 14 | 8 | 14 | 10 |
| 16 | 8 | 16 | 11 |
| 18 | 9 | 18 | 12 |
| 20 | 9 | 20 | 13 |
| 22 | 10 | 22 | 14 |
| 24 | 10 | 24 | 15 |
| 26 | 11 | 26 | 16 |
| 28 | 11 | 28 | 17 |
| 30 | 12 | 30 | 18 |
Как посчитать площадь земельного участка
Если участок имеет несколько форм, то его площадь вычисляется путем разбиения его на части и вычисления площадей каждой из них отдельно.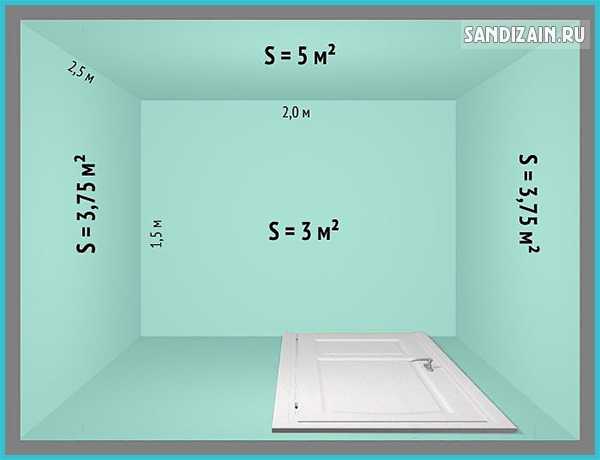
Если участок имеет форму прямоугольника, то площадь вычисляется по формуле:
S = a х b
где a и b – длина и ширина участка соответственно.
Если же участок имеет треугольную форму, то площадь считается по формуле:
S = (a х h) / 2
где a – основание, а h – высота.
Для участков нестандартной формы можно разбить их на части, каждую из которых можно вычислить по одной из формул выше, а затем сложить все полученные площади.
Также для точного измерения площади участка можно использовать геодезические приборы (тахеометр или нивелир). Они позволяют более точно измерять площадь.
Читайте также Что такое сотка земли
Геометрические вычисления
Геометрические вычисления – это математические расчеты, которые основываются на свойствах геометрических фигур. Эти вычисления могут быть использованы для решения различных задач, связанных с площадями, объемами, углами и другими характеристиками геометрических объектов.
Простые фигуры
Простые фигуры – это геометрические фигуры, у которых форма и размеры легко определяются и вычисляются.
Квадрат является прямоугольником с равными сторонами. Чтобы найти его площадь, нужно умножить длину одной стороны на длину другой. Формула для площади квадрата:
S = a², где “a” – длина стороны.
Прямоугольник – это фигура с противоположными сторонами, которые равны и параллельны друг другу. Чтобы найти его площадь, умножьте длину одной стороны на длину другой:
S = a х b, где “a” и “b” – длины сторон.
Треугольники
Треугольник – это фигура с тремя сторонами. Формула для площади треугольника:
S = 0.5 х a х h, где “a” – длина основания, “h” – высота.
Площадь круга
Круг – это фигура, которая состоит из всех точек, находящихся на одинаковом расстоянии от центра. Площадь круга вычисляется по формуле:
S = π х r², где “r” – радиус, “π” = 3.
14.Эти простые фигуры могут быть использованы для вычисления площади и объема различных объектов в нашей повседневной жизни, например, площади комнат, объема контейнеров, площади поля и т.д.
Калькулятор квадратных метров
Существует множество онлайн-калькуляторов квадратных метров, которые могут помочь в выполнении этих задач. Для расчета площади нужно ввести соответствующие размеры в единицах измерения (например, метры, сантиметры, дюймы и т.д.) и нажать кнопку “рассчитать”. В зависимости от конкретного калькулятора, он может также предоставить дополнительную информацию, например, количество материала, необходимого для покрытия данной площади.
Также существуют специализированные программы для компьютеров и мобильных устройств, которые позволяют выполнять более сложные геометрические вычисления и обработку данных, связанных с площадями. Все они могут значительно упростить и ускорить работу с площадями.
Но, как говорится – доверяй, но проверяй.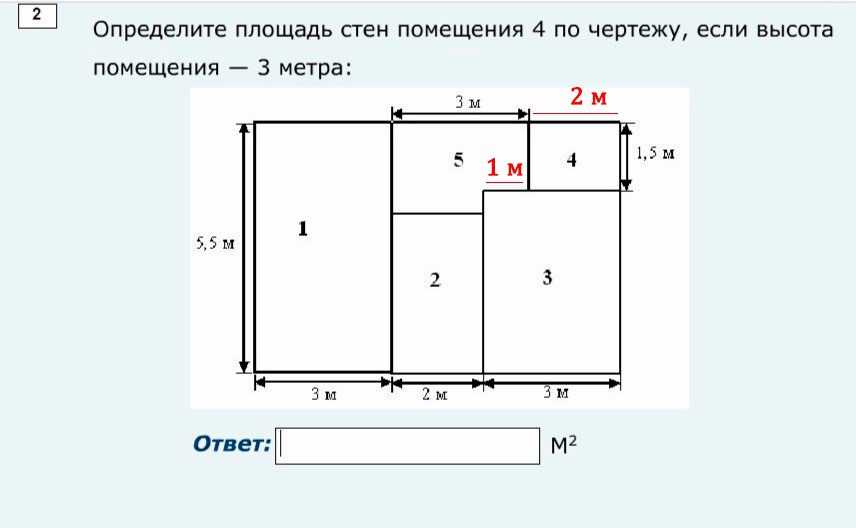
Поэтому не лишним будет проконтролировать машинные вычисления, вспомнив математику и геометрию.
| Площадь комнаты по полу | площадь стен при высоте потолка 2,5 метра | площадь стен при высоте потолка 2,7 метра | площадь стен при высоте потолка 3 метра |
|---|---|---|---|
| 10 кв.м | 31,7 | 34,2 | 38 |
| 11 кв.м | 33,3 | 36 | 40 |
| 12 кв.м | 35 | 37,8 | 42 |
| 13 кв.м | 36,3 | 39,2 | 43,5 |
| 14 кв.м | 37,5 | 40,5 | 45 |
| 15 кв.м | 40 | 43,2 | 48 |
| 16 кв.м | 41 | 44,3 | 49,2 |
| 17 кв.м | 42 | 45,4 | 50,4 |
| 18 кв.м | 43 | 46,4 | 51,5 |
| 19 кв.м | 43 | 47,3 | 52,5 |
| 20 кв.м | 45 | 48,6 | 54 |
21 кв. м | 46 | 49,7 | 55,2 |
| 22 кв.м | 47 | 50,8 | 56,4 |
| 23 кв.м | 48 | 51,8 | 57,6 |
| 24 кв.м | 50 | 54 | 60 |
| 25 кв.м | 51 | 55 | 61 |
Преобразование квадратного метра в разные единицы измерения
Преобразование в другие единицы измерения площади бывает нужным, например, при оценке земельного участка, расчете площади комнаты или стены. Вот несколько примеров преобразования квадратного метра в другие единицы измерения:
- Для перевода площади из квадратных метров в квадратные сантиметры, умножьте площадь в квадратных метрах на 10 000 (так как в одном квадратном метре содержится 10 000 квадратных сантиметров). Например, 5 квадратных метров = 5 * 10000 = 50 000 квадратных сантиметров.
- Для перевода в акры, нужно умножить площадь в квадратных метрах на 0.00024711 (так как один акр равен приблизительно 4046. 86 квадратных метров). Например, 50 квадратных метров = 50 * 0.00024711 = 0.0123555 акров.
- Для перевода квадратных метров в гектары, умножьте площадь в квадратных метрах на 0.0001 (так как один гектар равен 10 000 квадратных метров). Например, 5000 квадратных метров = 5000 * 0.0001 = 0.5 гектара.
86 квадратных метров). Например, 50 квадратных метров = 50 * 0.00024711 = 0.0123555 акров.Есть также множество онлайн-конвертеров, которые могут помочь в переводе площади из одной единицы измерения в другую.
В заключение можно сказать, что знание и умение работать с квадратными метрами — это необходимый навык не только для строителей и архитекторов. Когда мы знаем, как посчитать площадь комнаты или земельного участка, мы можем легче планировать свои будущие строительные или ремонтные работы, учитывать количество материалов и их стоимость, а также избежать ошибок и лишних расходов.
Видео Определить площадь стен комнаты
Так что не бойтесь математики и геометрии – они могут быть вашими лучшими помощниками в строительстве и ремонте.