Как рассчитать уклон кровли
Крыша является частью любого дома. Для неё очень важно подобрать качественный кровельный материал. Специалисты придерживаются мнения, что при его выборе следует учитывать угол наклона крыши, служащий для того, чтобы на ней не задерживалась вода. Уклоном кровли принято называть угол её наклона к горизонту. Выражается он обычно в процентах либо в градусах. Поэтому, чем больше его значение, тем крыша будет круче. О методиках расчёта данного показателя поговорим далее.
Виды крыш
В зависимости от угла наклона различают следующие конструкции крыши:
Стоит сказать, что плоская крыша не является полностью горизонтальной. Иначе бы вода с неё не стекала. У такой кровли угол наклона должен быть как минимум 30 градусов.
В зависимости от конструктивных особенностей выделяют три основные вида крыши:
Произвольными называют конструкции, для которых не рассчитывается нагрузка из-за воздействия ветра и атмосферных осадков. Подобные крыши обычно возводят только согласно пожеланиям хозяина. В них часто обустраиваются кладовки или даже жилые помещения.
Средние представляют собой самое лучшее соотношение угла ската крыши с учетом влияния атмосферных осадков и ветра. Такую кровлю лучше всего строить в регионах с повышенной влажностью.
Что касается малоуклонной крыши, то её конструкция выполнена таким образом, чтобы максимально снизить влияние на неё силы ветра. Кроме того, данное покрытие неплохо справляется с осадками. Подобные кровли устанавливаться практически в любом регионе.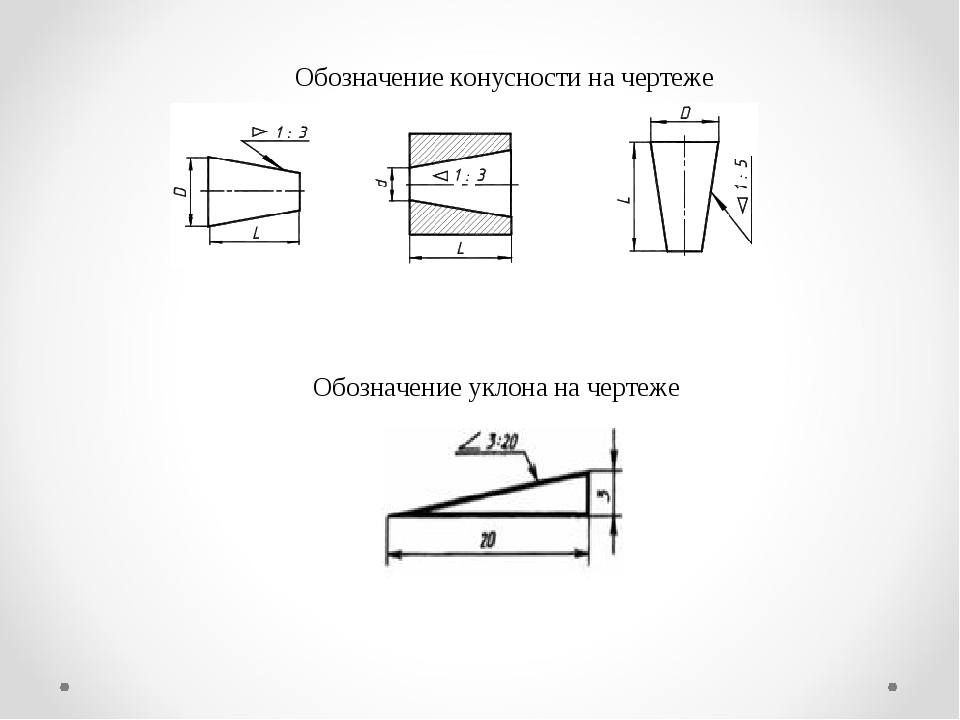
Ведь они имеют минимальный уклон и подходят практически под каждую конструкцию дома.
Кровля с малым уклоном имеет несколько серьезных достоинств, а именно:
Несмотря на то, что, возможно, придется потратиться на приобретение и установку дополнительных средств защиты от воды, неоспоримые достоинства окупят эти затраты.
От чего зависит уклон кровли
Угол наклона обычно определяют в зависимости от конструкции кровли, используемого кровельного материала, а также от климата региона, где будет строиться дом.
Для того чтобы знать, как в зависимости от величины угла наклона крыши выбирается кровельный материал, необходимо узнать, что влияет на этот показатель. К таким факторам относят:
- ветер,
- атмосферные осадки.
Рекомендации:
Если же этот показатель небольшой, то есть вероятность, что сильный порыв ветра в какой-то момент сорвет с поверхности кровельный материал.Единицы измерения
Сегодня наклон кровли в основном измеряется в градусах или процентах.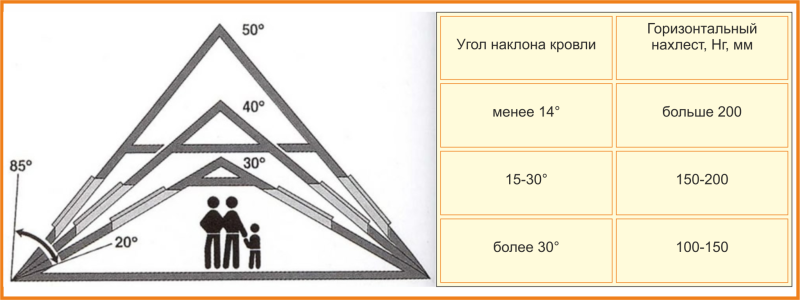
Правильный угол можно подобрать обеими системами. Чтобы узнать необходимое значение, можно взять за основу результаты замера самой крыши, а также уменьшенную модель, изображенную на бумаге. Нужный градус нужно закладывать еще при установке конструкции.
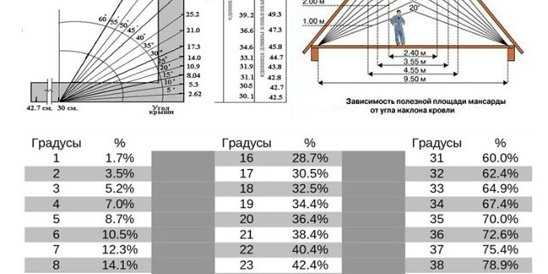
Рассмотрим, как вычислить уклон кровли в процентах. Необходимо взять высоту конька, разделить полученное значение на половину ширины дома, затем все следует умножить на 100%. В процентном соотношении 100% соответствует 45 градусам, а 1 градус равен 1,7%. Если в регионе, где возводится дом, возможен сильный ветер, то при расчетах угол наклона крыши рекомендуется делать минимальным. Для измерения и обозначения уклона кровли имеется специальный инструмент, который называется уклономером.
Как посчитать уклон кровли Использование схемы
Чтобы было проще, можно воспользоваться специальной схемой, которая позволяет подобрать материал кровли в зависимости от уровня её наклона. Здесь обозначен минимальный угол, соответствующий 0% и максимальный — 100%.
Значения в процентах нанесены на вертикальную шкалу. В центре схемы расположена полукруглая шкала, в которой имеются расчёты в градусах. Вообще, чем выше значение наклона, тем необходимо будет больше слоев материала на неё уложить. Кстати, количество нужного материала можно как раз определить по величине уклона крыши.
Рассмотрим, как расчёт уклона кровли влияет на выбор материала. Согласно приведенной схеме, если наклон составляет от 0 до 25%, то можно использовать для покрытия крыши рулонные материалы. При уклоне 0-10% настил рекомендуется укладывать в три слоя. Если это значение равно 10-25%, то можно положить один слой, например, материал с подсыпкой.
На крышах, уклон которых не более 28%, можно укладывать асбестоцементные волнистые листы, например, шифер. Если этот показатель до 29%, то рекомендуется использовать стальное покрытие. При уклоне 33% и выше, в качестве материала для кровли нередко используют черепицу.
Расчет по формуле
Когда определён уклон кровли и нужный материал для покрытия, необходимо рассчитать высоту конька.
Для этого можно использовать простой математический способ: необходимо взять ширину пролета дома и разделить её на два. Результат частного нужно умножить на относительную величину, которая вычисляется с помощью специальной таблицы Брадиса. В ней указаны значения для каждого угла.
Теперь приведем пример расчета уклона кровли. Если ширина пролета составляет 8 метров и угол наклона крыши 25 градусов, то высота конька получается следующей: 8:2=4 4*0,47=1,88 метров.
Считая в обратную сторону по этой же формуле можно определить угол наклона крыши. При строительстве это вряд ли понадобится, зато может пригодиться во время ремонта.
Использование уклономера
Величину уклона можно ещё вычислить при помощи специального инструмента, который называется уклономером. Он представляет собой рейку с прикреплённой к ней рамкой. Между планками расположена ось, к которой закрепляется маятник. Внутри выреза имеется шкала с делениями. Когда рейка лежит горизонтально, то соответствует нулю на шкале.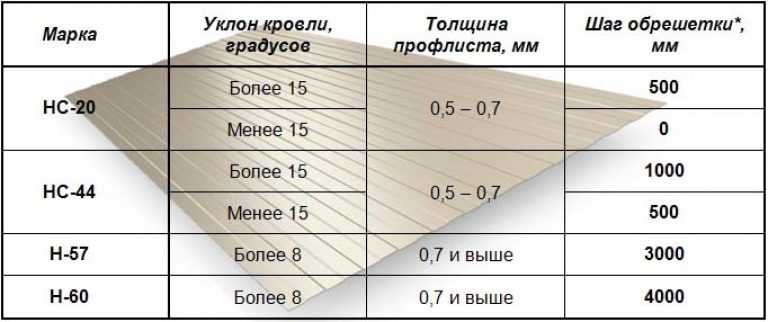
Теперь узнаем, как считать уклон кровли при помощи этого инструмента:
Оптимальный уклон кровли для разных материалов
Важно! Стоит понимать, что все значения, которые здесь указаны, являются всего лишь рекомендациями. Поэтому каждый вправе выбирать угол наклона крыши к горизонту на свое усмотрение. Некоторые строители забывают о такой очень важной детали, как планирование водостока, а ведь именно через него вода стекает с крыши.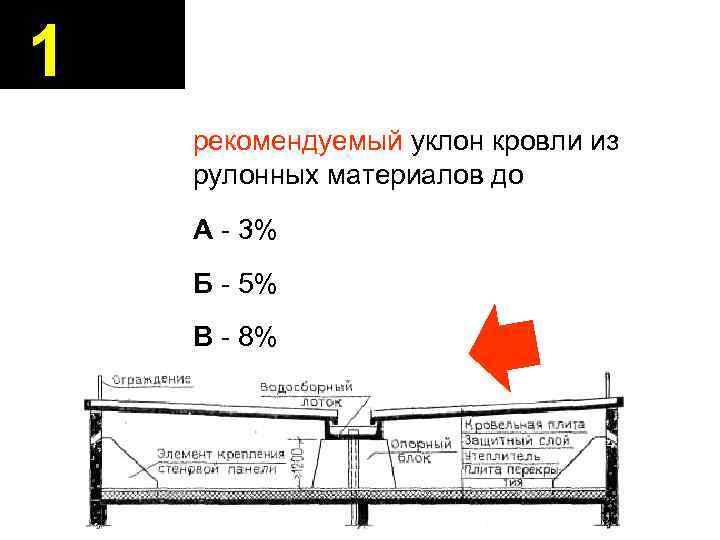
Если не позаботиться об этом заранее, то после строительства кровли могут возникнуть трудности с отведением воды.
минимального, оптимального, как посчитать уклон и какой должен быть угол
Профессионалы строители знают, что процесс постройки кровли иногда может притормаживаться из-за того, что необходимо выбрать «правильный материал» и произвести точный расчет угла наклона крыши. Эти два вопроса являются тесно взаимосвязанными, ведь от угла наклона кровли зависит и выбор материала для ее покрытия.
Напоминаем, что крыши бывают одно-, двух- и четырехскатными, это зависит от того, сколько скатов для своей крыши вы выбираете, а величина наклона угла скатов будет определяться.
Какие факторы влияют на расчет уклона крышиНапример, угол наклона стандартной кровли с одним скатом составляет от 9 до 60 градусов – это зависит от следующих факторов:
- Материал, выбранный для крыши;
- Климатические и атмосферные условия;
- Назначение строения.
Если у крыши два, или более скатов, то тут значение имеет не только регион, в котором находится здание, но и то, зачем нужен чердак. Например, если вы используете чердак не как жилое помещение, а как хранилище для старых вещей, то потребность строить его широким и высоким отпадает. А вот если вы желаете, чтобы чердак стал полноценным жилым мансардным помещением, то тут нужно делать плотную кровлю и знать, как рассчитать угол наклона крыши. В данном случае расчёт угла наклона крыши зависит от таких факторов:
- Первый – дизайн самого здания и помещения.
- Второй – выбор материалов для крыши.
- Третий – условия климата региона.
В регионах с сильными ветрами желательнее строить крышу с минимальным уклоном – материал не должен подвергать сильной ветровой нагрузке. Тоже самое говорят и о солнечной местности, где больше всего жарких дней в году – в солнечных регионах как раз меньше всего осадков.
В тех регионах, где осадков много (включая дожди, грады и снегопады), угол наклона кровли следует делать большой до 60 градусов, ведь только такой наклон снизит нагрузку от снега, талых вод и разного рода мусора.
Итак, давайте разберемся, как посчитать угол наклона крыши. Нам нужно принять во внимание все факторы, которые были описаны выше, поэтому расчет уклона кровли осуществляется в диапазоне от 9 до 60 градусов. Интересно, что подобный расчет обычно приводит к одному оптимальному решению — 20 — 35 градусов.
При таком уклоне используют любой материал для кровли – профильный настил, металлочерепицу, куски шифера и т.д.
Если кровлю покрывают металлочерепицейУ всех материалов есть определенный список требований, который к ним предъявляются во время возведения конструкции.
Известно, что у металлочерепицы немалый вес, по сравнению с иными материалами. Вот из-за чего важно сделать правильный расчет уклона кровли с металлочерепицей, который должен быть оптимально низким.
Важно учитывать данное требование в регионе с большим количество ветров и ураганов. Следовательно, угол наклона должен быть максимально низким. Из-за большого значения угла наклона крыша может вздуться, из-за чего, в свою очередь, увеличится давление на несущую конструкцию кровли. А увеличенное давление преждевременно разрушит кровлю.
В среднем, для крыш, которые будут покрываться данным материалом, среднее оптимальное значение угла наклона – это 27 градусов. Следовательно, ваш дом будет защищен от просачивания дождевой воды и снега.
Минимальный же угол наклона кровли – это всего 14 градусов. Если будет использована мягкая черепица, то угол наклона может быть 11 градусов, но крыша должна быть обязательно подрешечена дополнительно.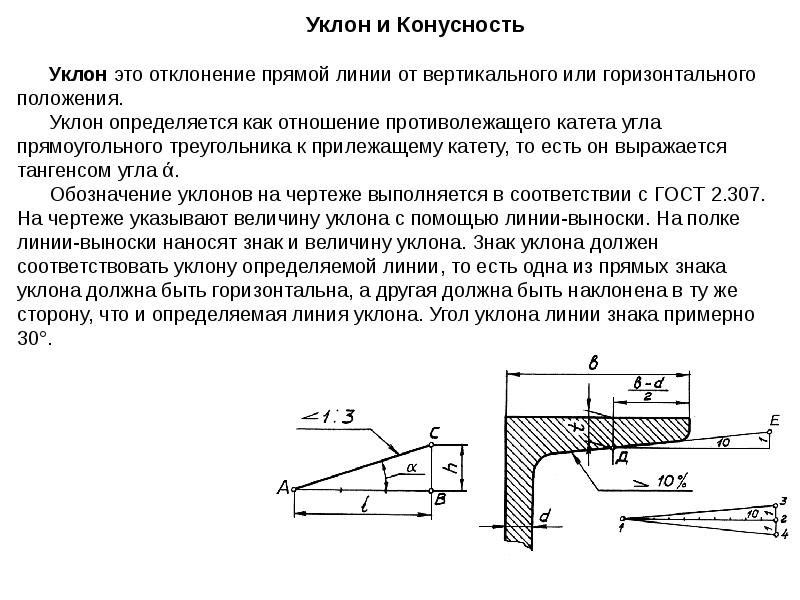
Профнастил – это самый ходовой материал для кровли – у него маленький вес, он прочен, крепится и монтируется довольно легко.
Уклон крыши с профнастилом и нагрузки.
Производители профнастила рекомендуют делать угол наклона крыши не менее 12 градусов.
Если кровля покрывается различным мягким материаломК такому материалу отнесем рубероид, ондулин, полимерное (мембранное) кровельные покрытие.
У такой кровельной конструкции нужно делать угол наклона от 6 до 15 градусов – значение меняется от количества слоев мягкого материала.
Например, если покрытие двуслойное, то угол наклона принимаем равным до 15 градусов, а вот, если трехслойный, то значение можно уменьшить до 3-5 градусов.
А вот мембранное покрытие можно использовать на любых крышах, любого состояния, в любых условиях, тут уже угол наклона можно убавить до 2- 5 градусов.
Из всего вышесказанного делаем вывод — то как посчитать уклон кровли, решает сам хозяин постройки.
Однако, учитываем определенную зависимость: крыша должна выдерживать не только временные, но и постоянные нагрузки. К «временным» относятся — дождь, ветер и вес, который они оказывают на покрытие кровли, постоянная нагрузка – это вес кровельного покрытия и материала.
Величина наклона крыши определяет тип обрешетки, шаг. У кровли с низким наклоном шаг обрешетки должен быть максимально коротким. Для кровли с минимальной величиной шаг обрешетки составляет 35-45 см.
Также всех занимает один вопрос – сколько кровельного материала нужно приобретать.
Уклон кровли из мягких материаловЧем больше угол наклона кровли вы делаете, тем больше материала нужно будет израсходовать.
Чем больше угол наклона кровли вы делаете, тем больше материала нужно будет израсходовать.
Если же придерживаться всех указанных требований, то можно сделать крышу, которая прослужит не один десяток лет! Все приведенные требования и факторы помогают понять, как рассчитать уклон кровли.
Однако, напоминаем, что для каждого дома расчет производится индивидуально.
Напоследок дадим вам несколько полезных советов, которые помогут вам выбрать кровельный материал:
Итак, если уклон кровли у вас маленький, до 10 градусов, то крыть крышу можно даже каменной крошкой, гравием (рассчитываем 5 мм для крыши и 15 мм для гравия).
Если угол наклона вашей крыши составляет 10 и более градусов, то применяем базовую битумную гидроизоляцию. Применяя рулонный материал, не забываем о дополнительном защитном покрытии, которым может быть обычная покраска.
Если вы задумали покрыть кровлю профнастилом, нужно герметизировать стыковые швы. Стыки обязательно должны быть двойными.
Как рассчитать угол наклона крыши?Как правило, чтобы знать, как посчитать уклон крыши, нужно знать, на какую высоту вы задерете конек (а высота крыши с коньком зависит напрямую от того, для чего предназначен чердак). Итак, если из чердака вы делает жилую мансарду, то считаем действительными следующие расчёты.
Определяем ширину фронтона – кровельного торца, к примеру, пусть 6 м. Разделяем ширину пополам: 6:2= 3 м, а по стандарту высота крыши в коньке составляет 1,8 метра.
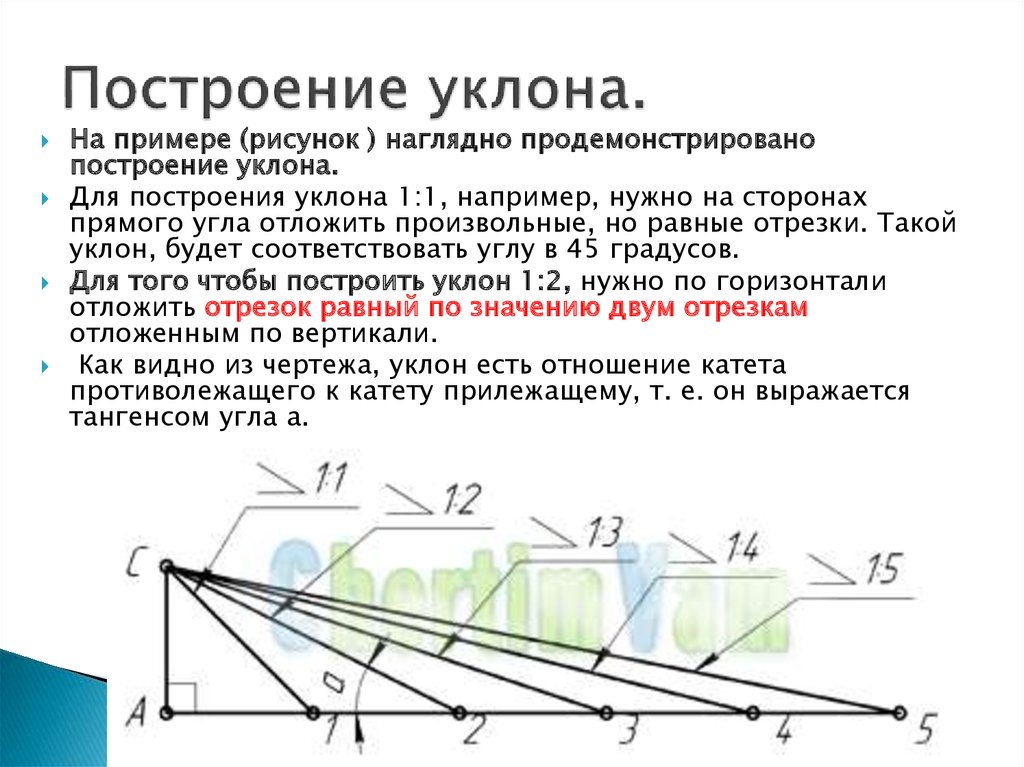
Далее, вспоминаем общий курс геометрии – отношение прилежащего катета к противолежащему в треугольнике – это ни что иное, как тангенс угла. Составляем формулу и находим значение тангенса:
tg A=a:b=3:1,8=1,67
Берем таблицу Брадиса и находим примерное значение – если tg A=1,67 , то угол наклона будет приблизительно 58-59 градусов. Мы можем принять максимальное значение угла – 60 градусов. Это и будет наш искомый угол наклона кровли.
Пример для расчета угла наклона крышиУклон любой крыше придается в соответствии с климатическими условиями и структурой здания. Обилие атмосферных осадков заставляет делать наклон крыши крутым и наоборот. В целом, надо помнить, что до того как вычислить угол наклона крыши, учтите, что наклон кровли может колебаться от 10 до 60°. Чем круче кровля, тем больше материала вы потратите.
Уклон стропил, либо высоту конька определяют математическим путем, либо мерилами.
Известно, что крыши с наклоном в 35-45 градусов не делают, поскольку такой диапазон создаст все условия для накопления снега в зимнее время, да и ветры такие кровли плохо переносят. Монолитной крышу сделать невозможно, поэтому материал укладывается со стыками. Стык – это место с повышенной коррозийной опасностью, поэтому им уделяется особое внимание во время расчетов. Также во время ураганы в щели могут забиться листья и ветки, которые потом разбухнут, а крыша испортится. Создаются отверстия для проникновения дождя и снега, крыша рушится.
Во время подсчета наклона кровли, помните не только об экономии (стоимость стропил, материала, работы), но и об эксплуатационных качествах. Если кровлю установить по всем правилам, она обойдется дороже, зато дома вам будут обеспечены тепло и сухость, что в итоге помогает сберегать значительные суммы денег на ремонтах. Тут как раз играет роль правильно подобранный угол наклона кровли!
Как использовать формулу наклона и найти наклон линии, независимо от того, является ли наклон положительным, отрицательным или неопределенным.
Рабочий лист по наклону линии
Апплет наклона (html5)
Калькулятор формулы уклона (бесплатный онлайн-инструмент для расчета уклона по 2 точкам)
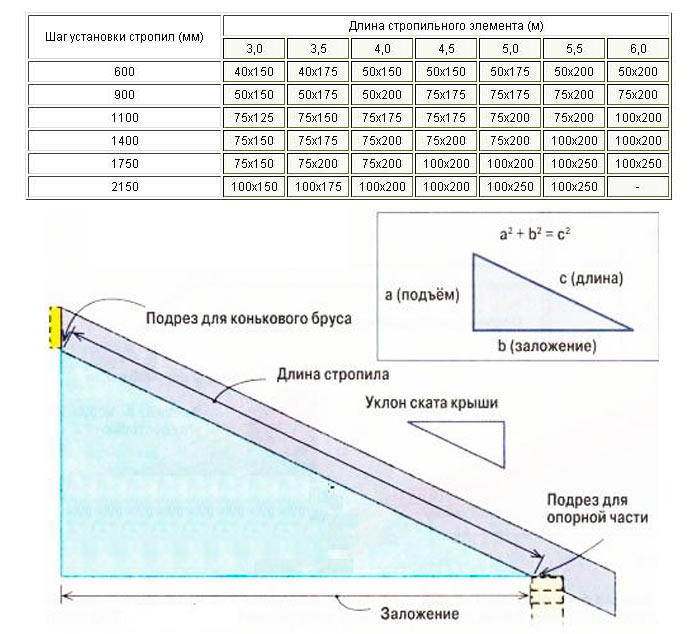
Наклон линии характеризует направление линии. Чтобы найти наклон, вы делите разницу координат y двух точек на прямой на разницу координат x тех же двух точек.
Разные слова, та же формула
Учителя используют разные слова для координат y и координат x.
- Некоторые называют координаты у подъемом, а координатами х — бег.
- Другие предпочитают использовать нотацию $$\Delta$$ и называть y-координаты $$\Delta y$$ , а x-координаты $$\Delta x$$ .
Все эти слова означают одно и то же , то есть значения y находятся вверху формулы (числитель), а значения x внизу формулы (знаменатель)!
Пример 1
Наклон линии , проходящей через точку (1, 2) и точку (4, 3), равен $$ \frac{1}{3}$$.
Помните: разница в значениях y идет в числителе формулы, а разница в значениях x идет в знаменателе формулы.
Может ли любая из точек быть $$( x_1 , y_1 ) $$ ?
Есть только один способ узнать!
Во-первых, мы будем использовать точку (1, 2) как $$x_1, y_1$$, и, как вы можете видеть: наклон: $ \boxed {\frac{1}{3} }$ .
Теперь давайте используем точку (4, 3) как $$x_1, y_1$$, и, как вы можете видеть, наклон упрощается до того же значения: $ \boxed {\frac{1}{3} }$ .
Работа рядом
точка (4, 3) как $$ (x_1, y_1 )$$
Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{3-2}{4-1} = \frac{1}{3} $$
точек (1, 2) как $$ (x_1, y_1 )$$
Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{2-3}{1-4} = \frac{-1}{- 3} = \frac{1}{3} $$
Ответ: , а не не имеет значения, какую точку поставить первой.
Пример 2 наклона линии А
Наклон линии , проходящей через точки (3, 4) и (5, 1), равен $$- \frac{3}{2}$$, потому что каждый раз, когда линия опускается на 3 (изменение y или подъем) линия смещается вправо (разбег) на 2.
Эта страница:
- Формула
- Пример
- Видео
- Заказать?
- Любые две точки определяют наклон линии?
- Наклон вертикальной линии
- Наклон горизонтальной линии
- Практические задачи
youtube.com/embed/JYZU1B5zOjg?hl=en&fs=1″ frameborder=»0″ allowfullscreen=»»> Наклон вертикальных и горизонтальных линий
Наклон вертикальной линии не определен
Это связано с тем, что любая вертикальная линия имеет $$\Delta x$$ или «пробег» нуля. Всякий раз, когда ноль является знаменателем дроби в этом случае дроби, представляющей наклон линии, дробь не определена. На рисунке ниже показана вертикальная линия (x = 1).
Наклон горизонтальной линии равен нулю
Это потому, что любая горизонтальная линия имеет $$\Delta y$$ или «подъем» нуля. Следовательно, независимо от того, каков пробег (при условии, что он не равен нулю!), дробь, представляющая уклон, имеет в числителе ноль.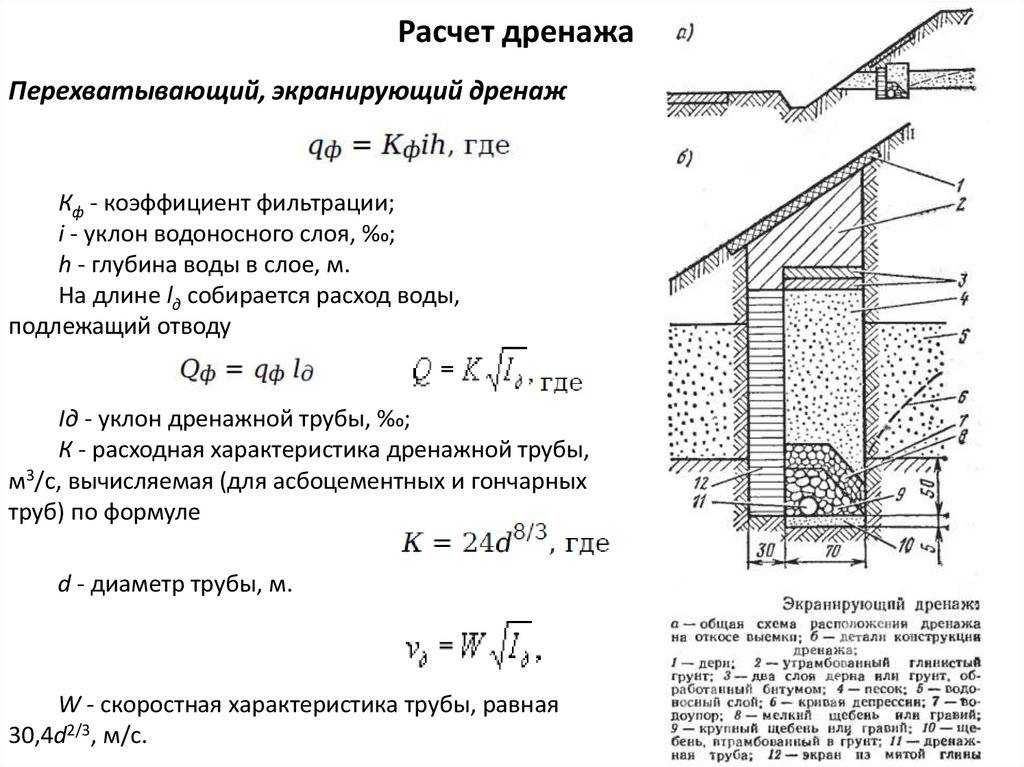
Любые две точки на прямой имеют одинаковый наклон?
Ответ: Да, и это фундаментальный момент, который следует помнить при расчете уклона.
Каждая линия имеет постоянный наклон. Другими словами, наклон линии никогда не меняется. Эта фундаментальная идея означает, что вы можете выбрать 90 123 любых 90 124 2 точек на линии.
Подумайте об идее прямой линии. Если бы наклон линии изменился, то это была бы зигзагообразная линия, а не прямая линия, как вы можете видеть на рисунке выше.
Наклон линии
Никогда не меняетсяЭта страница:
- Формула
- Пример
- Видео
- Заказать?
- Любые две точки определяют наклон линии?
- Наклон вертикальной линии
- Наклон горизонтальной линии
- Практические задачи
Рабочий лист по наклону линии
Апплет наклона (html5)
Калькулятор формулы уклона (бесплатный онлайн-инструмент для расчета уклона по 2 точкам)
Практика ПроблемыПроблема 1
Каков наклон прямой, проходящей через точки (10,3) и (7, 9)?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ (10,3)}$$ как $$x_1, y_1$$
$ \frac{9- \red 3}{7- \red{10}} \\ = \frac{6}{-3} \\ = \ в коробке {-2 } $
Используя $$ \red{ (7,9)} $$ как $$x_1, y_1$$
$ \frac{3- \red 9{10- \красное 7} \\ =\ гидроразрыв{-6}{3} \\ = \в коробке{-2} $
Проблема 2
Прямая проходит через (4, -2) и (4, 3).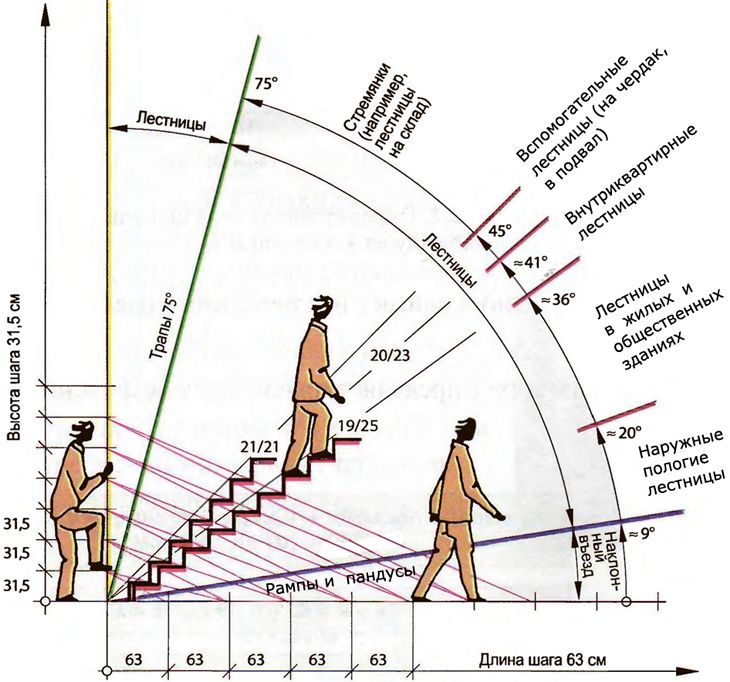
Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 4,3 )}$$ как $$x_1, y_1$$
$ = \frac{-2 — \red 3}{4- \red 4} «=» \frac{-5}{\color{red}{0}} \\ = \text{неопределенный} $
Используя $$ \red{ ( 4, -2 )}$$ как $$x_1, y_1$$
$ = \frac{3- \red{-2}}{4- \red 4} «=» \frac{5}{\color{red}{0}} \\ = \текст{неопределенный} $
Всякий раз, когда длина линии равна нулю, наклон не определен. Это потому, что в знаменателе наклона стоит ноль! Любой наклон любой вертикальной линии не определен.
Проблема 3
Прямая проходит через (2, 10) и (8, 7).
Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 8, 7 )}$$ как $$x_1, y_1$$
$ \frac{10 — \red 7}{2 — \red 8} \\ = \ гидроразрыва {3}{-6} \\ = -\фракция{1}{2} $
Используя $$ \red{ ( 2,10 )}$$ как $$x_1, y_1$$
$ \frac{7 — \red {10}}{8- \red 2} \\ = \ гидроразрыв {-3} {6} \\ = -\фракция{1}{2} $
Проблема 4
Прямая проходит через (7, 3) и (8, 5). Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ (7,3 )}$$ как $$x_1, y_1$$
$$ \frac{ 5- \red 3}{8- \red 7} \\ = \ гидроразрыва {2} {1} \\ = 2 $$
Используя $$ \red{ ( 8,5 )}$$ как $$x_1, y_1$$
$$ \frac{ 3- \red 5}{7- \red 8} \\= \фракция{-2}{-1} \\ = 2 $$
Проблема 5
Прямая проходит через (12, 11) и (9, 5) .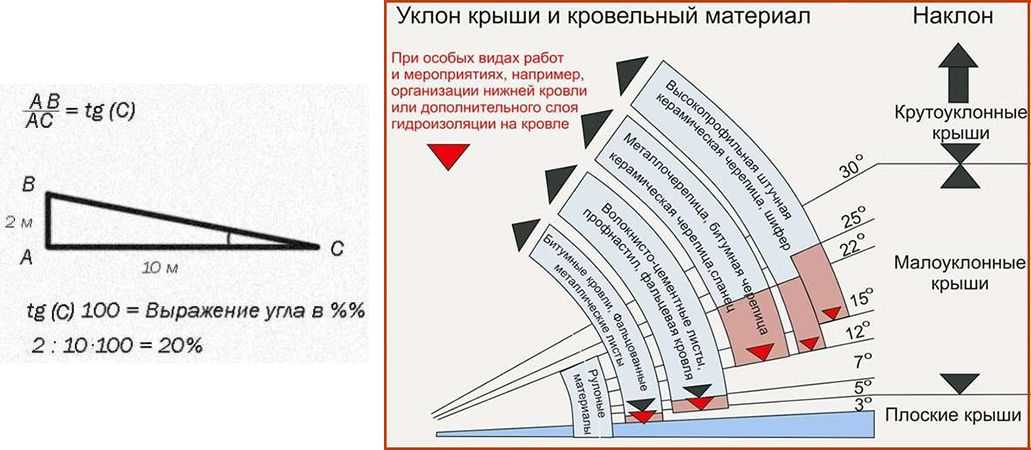
Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 5, 9)}$$ как $$x_1, y_1$$
$$ \frac{ 11 — \red 5}{12- \red 9} \\ = \ гидроразрыва {6} {3} \\ =2 $$
Используя $$ \red{ (12, 11 )}$$ как $$x_1, y_1$$
$$ \frac{ 5- \red{ 11} }{9- \red { 12}} \\ = \фракция{-6}{-3} \\ = 2$$
Проблема 6
Каков наклон линии, проходящей через (4, 2) и (4, 5)?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 4,5 )}$$ как $$x_1, y_1$$
$$ \frac{ 2 — \red 5}{4- \red 4} \\ = \frac{-3}{\color{red}{0}} \\ = не определено $$
Используя $$ \red{ ( 4,2 )}$$ как $$x_1, y_1$$
$$ \frac{ 5 — \red 2}{4- \red 4} \\ = \frac{ 3}{\color{red}{0}} \\ = не определено $$
ПРЕДУПРЕЖДЕНИЕ! Уловите ошибку в следующей задаче: Дженнифер пыталась найти наклон, проходящий через точки $$(\color{blue}{1},\color{red}{3})$$ и $$ (\color {синий}{2}, \цвет{красный}{6})$$ .
У нее были небольшие проблемы с применением формулы наклона, она пыталась вычислить наклон 3 раза и дала 3 разных ответа. Сможете ли вы определить правильный ответ?
Задача-вызов
Найдите наклон прямой через две точки.
Попытка №1
$ наклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} «=» \ гидроразрыв {6-3} {1-2} \\= \фракция{3}{-1} =\в коробке{-3} $
Попытка #2
$$ наклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} «=» \фракция{6-3}{2-1} \\= \фракция{3}{1} \\ = \в коробке{3} $$
Попытка №3
$$ уклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} \\ =\ гидроразрыва {2-1} {6-3} \\ =\в коробке{ \frac{1}{3}} $$
Правильный ответ — попытка №2.
В попытке №1 она не всегда использовала очки. В первой попытке она сделала следующее:
$$ \frac{\color{red}{y{\boxed{_2}}-y_{1}}}{\color{blue}{x\boxed{_{1}}-x_{2}}} $$
Проблема с попыткой №3 заключалась в обратном подъеме и беге. Она поместила значения x в числитель (сверху), а значения y в знаменатель, что, конечно же, противоположно!
$$ \ отмена {\ frac {\ color {синий} {x_ {2} -x_ {1}}} {\ color {red} {y_ {2} -y_ {1}}}} $$
Тренировка склонов Генератор проблем Вы можете сколько угодно практиковаться в решении подобных задач с помощью приведенного ниже генератора задач на уклон.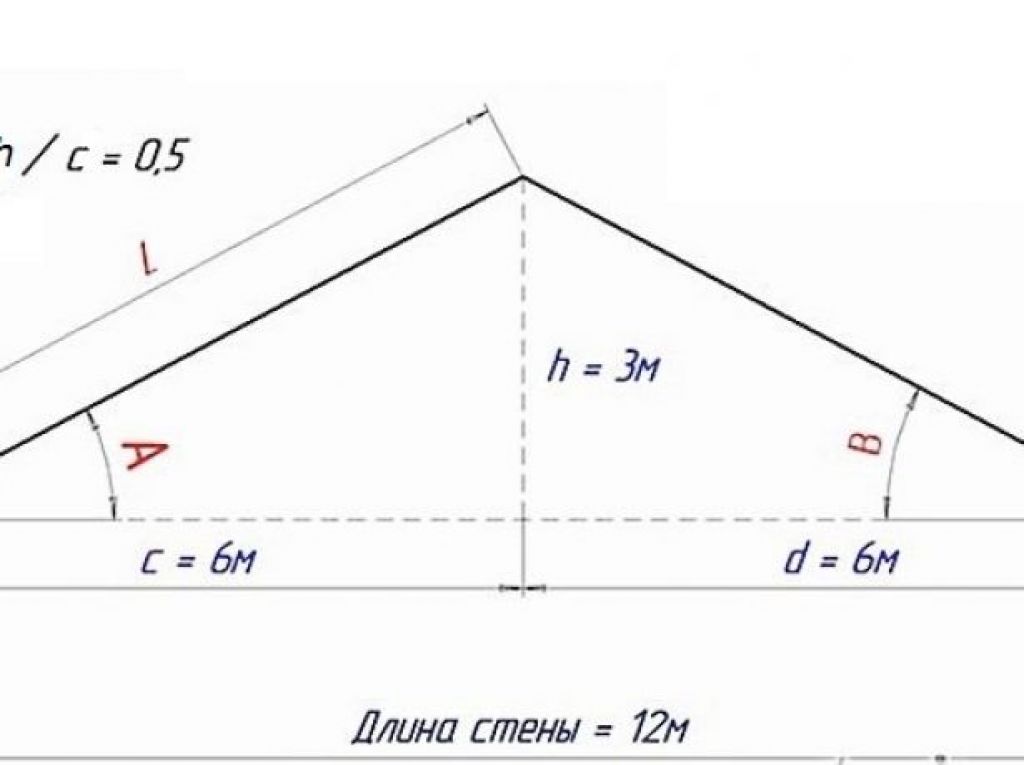
Он будет случайным образом генерировать числа и запрашивать наклон линии через эти две точки. Вы можете выбрать, насколько большими будут числа, регулируя уровень сложности.
Рабочий лист по наклону линии
Апплет наклона (html5)
Калькулятор формулы уклона (бесплатный онлайн-инструмент для расчета уклона по 2 точкам)
Algebra 1 Help
Студенты, нуждающиеся в помощи по алгебре 1, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по Алгебре 1. Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы мгновенно получите много помощи по Алгебре 1. Получите помощь сегодня с нашей обширной коллекцией необходимой информации по алгебре 1.
Алгебра 1
Распределительная собственность
Как использовать FOIL в дистрибутивной собственности
Как использовать метод сетки для FOIL
Уравнения / Неравенства
Системы уравнений
Уравнения/наборы решений
Как разложить уравнение на множители
Как найти решение set
Как найти решение системы уравнений
Линейные/рациональные уравнения/уравнения с переменными
Как узнать, когда уравнение не имеет решения
Как найти решение рационального уравнения с LCD
Как найти решение уравнения
Квадратные уравнения
Как разложить квадратное уравнение на множители
Как найти решение квадратного уравнения
Системы неравенств
Как найти решение неравенства со сложением
Как найти решение неравенства с делением
Как найти решение неравенства с умножением
Как найти решение неравенства с вычитанием
Функции и линии
Алгебраические функции
Как найти прямой вариант
Как найти f(x)
Как найти обратную вариацию
Как найти домен функции
Как использовать квадратичную функцию
Уравнения прямых
Формула средней точки
Как найти концы отрезка
Как найти середину отрезка
Параллельные линии
Как узнать, параллельны ли прямые
Как найти уравнение параллельной прямой
Как найти наклон параллельных прямых
Перпендикулярные линии
Как узнать, перпендикулярны ли прямые
Как найти уравнение перпендикулярной прямой
Как найти наклон перпендикулярных линий
Точки и формула расстояния
Как узнать, находится ли точка на прямой с уравнением
Как найти длину линии по формуле расстояния
Уравнения наклона и линии
Как найти наклон линии
Как найти уравнение прямой
Графика
Как построить график функции
Как построить линию
Как нарисовать точку
Как построить график квадратичной функции
Как построить график двухшагового неравенства
Как построить график функции абсолютного значения
Как построить график экспоненциальной функции
Как построить график упорядоченной пары
последовательности
Как найти последовательные целые числа
Как найти ответ на арифметическую прогрессию
Как найти общее различие в последовательностях
Как найти следующий член арифметической прогрессии
Как найти n-й член арифметической прогрессии
Линейные уравнения
Преобразование измерений
Как решать уравнения абсолютного значения
Как решить одношаговые уравнения
Как решать двухшаговые уравнения
Как писать выражения и уравнения
Проценты
Пропорции
Линейные неравенства
Неравенства абсолютного значения
Графические неравенства
Запись неравенств
Проценты
Десятичные числа и проценты
Как найти десятичный эквивалент процента
Как найти процент, эквивалентный десятичной дроби
Дроби и проценты
Как найти дробь от процента
Как найти дробные проценты
Как найти процент от дроби
Денежный процент
Как найти размер прибыли
Как найти простые проценты
Как найти сумму налога с продаж
Как узнать цену продажи
Процент изменения
Как найти процент уменьшения
Как найти процент увеличения
Целиком и частично
Как найти часть от целого в процентах
Как найти целое из части с процентами
Реальные числа
Подсчет/наборы
Как найти недостающее число в наборе
Как найти количество целых чисел между двумя другими целыми числами
Целочисленные операции
Как складывать целые числа
Как делить целые числа
Как умножать целые числа
Как вычитать целые числа
Количество линий и абсолютное значение
Как найти абсолютное значение
Как найти значение с числовой строкой
Как построить график неравенства с числовой прямой
Как построить дроби на числовой прямой
Статистика и вероятность
Как найти межквартильный размах
Как найти среднее
Как найти медиану
Как найти режим
Как найти диапазон
Как найти стандартное отклонение
Переменные
мономы
Как делить одночленные частные
Как умножить одночлен на многочлен
Как умножать одночленные частные
Многочлены
Биномы
Как найти решение рационального уравнения с биномиальным знаменателем
Как найти решение биномиальной задачи
Как найти значение коэффициента
Как умножать биномы с распределительным свойством
Как упростить биномы
Факторные полиномы
Как разложить многочлен на множители
Как факторизовать переменную
Полиномиальные операции
Как складывать полиномы
Как делить многочлены
Как найти степень многочлена
Как умножать многочлены
Как вычитать многочлены
Трехчлены
Как складывать трехчлены
Как делить трехчлены
Как разложить трехчлен на множители
Как умножать трехчлены
Как вычитать трехчлены
Алгебра I часто впервые знакомит учащихся с процессами вычисления переменных, понимания неравенств и использования порядка операций для упрощения выражений.
Некоторым учащимся часто бывает трудно освоить эти новые навыки; однако усердная практика основных алгебраических принципов жизненно важна для успеха в дальнейших курсах математики. Понимание геометрии, предварительного исчисления, исчисления и высшей математики, физики и химии требует фундаментального понимания того, как упростить выражения и манипулировать переменными. Нужны ли вам лучшие репетиторы по алгебре 1 в Бостоне, репетиторы по алгебре 1 в Детройте или лучшие репетиторы по алгебре 1 в Далласе, Форт-Уэрт, работа с профессионалом может вывести ваше обучение на новый уровень.
В общем, Алгебра I фокусируется на основах понимания и упрощения задач. Учащиеся работают над тем, чтобы логически продумать этапы решения проблемы, не делая немедленных выводов или решений. Кроме того, учащихся учат объяснять отношения между уравнениями, давать словесные описания графиков, таблиц и диаграмм и предсказывать форму фигур на основе математических соотношений. Репетиторы Varsity Tutors предлагают такие ресурсы, как бесплатные практические тесты по алгебре 1, которые помогут вам в самостоятельном обучении.
Общие темы по алгебре I включают:
Арифметика с полиномиальными и рациональными выражениями: учащимся предлагается упростить числовые выражения с помощью порядка операций, разложить переменные в числовые уравнения и упростить сложные выражения с помощью различных комбинаций чисел и переменных.
Создание выражений: используя графики и таблицы в качестве ориентира, учащимся предлагается определить взаимосвязь между двумя или более переменными. Например, учащимся может быть предоставлена таблица пройденного расстояния и времени, необходимого для преодоления этого расстояния. Ожидается, что учащиеся определят, как пройденное расстояние влияет на затраченное время (удвоение пройденного расстояния требует удвоения времени при той же скорости).
Рассуждения с помощью уравнений и неравенств: учащиеся, изучающие алгебру I, должны найти значение переменных, упрощая числовые выражения.
Кроме того, студентов учат, как графически отображать эти решения в системах координатной плоскости. Также рассматриваются неравенства и определение того, как будет затеняться график системы координат на основе численного решения.Видение структуры в выражении: использование рассуждений с уравнениями и неравенствами в качестве основы, учащихся учат писать алгебраические выражения и неравенства на основе графиков, а иногда и таблиц данных.
Кроме того, студентов учат, как графически отображать эти решения в системах координатной плоскости. Также рассматриваются неравенства и определение того, как будет затеняться график системы координат на основе численного решения. Ключом к успеху в алгебре I является постоянная практика. В то время как некоторые учащиеся будут иметь опыт упрощения выражений, добавление графиков, диаграмм, неравенств и факторизации будет новым для других. Общие стратегии достижения успеха включают просмотр кратких резюме в учебниках перед выполнением домашних заданий и отработку дополнительных 10–15 заданий после выполнения назначенных отрывков домашнего задания. Часто учащиеся изучают шаблоны, необходимые для решения задач, путем постоянного повторения вместо того, чтобы читать разделы книги.