Задачи на нахождение площади. Математика 4 класс.
Математика 4 класс
- Математические диктанты
- Тесты
- Нестандартные задачи
- Логические задачи
- Задачи с ответами
- Примеры
Контрольные работы
- Числа, которые больше 1000. Нумерация
- Итоговая контрольная работа за 1 четверть
- 1 четверть
- 2 четверть
- Итоговая контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Деление на двузначное число
- Итоговые контрольные работы за курс начальной школы
- Контрольная работа 1
Задача 1
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Решение:
- 1) 8 ∙ 7 = 56
Ответ: Площадь прямоугольника 56 м². 
Задача 2
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Решение:
- 1) 1) 64 : 8 = 8 (сторна витрины)
- 2) 2) 8 ∙ 4 = 32 (периметр витрины)
- Ответ: 32 м.
Задача 3
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Решение:
- 1) 1) 90 ∙ 7 = 630
- Ответ: 630 см².
Задача 4
Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Решение:
- 1) 48 ∙ 30 = 1440 (площадь первого участка)
- 2) 30 + 6 = 36 (ширина второго участка)
- 3) 1440 : 36 = 40
- Ответ: длина второго участка 40 м.

Задача 5
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Решение:
- 1) 36 ∙ 20 = 720 (площадь первого участка)
- 2) 36 – 6 = 30 (длина другого участка)
- 3) 720 : 30 = 24
- Ответ: ширина другого участка 24 м.
Задача 6
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Решение:
- 1) 4 ∙ 4 = 16 (площадь квадрата)
- 2) 2 ∙ 6 = 12 (площадь прямоугольника)
- 3) 16 — 12 = 4
- Ответ: площадь квадратата больше на 4 см.
Задача 7
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Узнайте площадь и периметр квадрата.
Решение:
- 1) 6 ∙ 6 = 36
- 2) 6 ∙ 4 = 24
- Ответ: площадь квадрата 36 см², периметр квадрата 24 см.
Задача 8
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Решение:
- 1) 7 ∙ 5 = 35
- 2) 7 ∙ 2 = 14
- 3) 5 ∙ 2 = 10
- 4) 10 + 14 = 24
- Ответ: площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 9
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
- 1) 8 ∙ 8 = 64 (площадь клумбы)
- 2) 64 : 16 = 4(1/16 клумбы)
- 3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
- 4) 64 – 28 = 36
- Ответ: незабудками засажено 36 м².

Задача 10
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Решение:
- 1) 6 ∙ 2 = 12
- 2) 18 – 12 = 6
- 3) 6 : 2 = 3 (ширина прямоугольника)
- 4) 3 ∙ 6 = 18
- Ответ: площадь прямоугольника 18 м².
Задача 11
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
- 1) 4800 : 60 = 80 (длина стола)
- 2) 60 ∙ 2 = 120 см
- 3) 80 ∙ 2 = 160 см
- 4) 120 + 160 = 280 см
- Ответ: периметр стола 280 см.
Задача 12
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
- 1) 5 ∙ 2 = 10
- 2) 40 – 10 = 30
- 3) 30 : 2 = 15 (другая сторона прямоугольника)
- 4) 5 ∙ 15 = 75
- Ответ: площадь прямоугольника 75 см².

Задача 13
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
- 1) 49 : 7 = 7 (сторона квадрата)
- 2) 7 ∙ 4 = 28 (периметр квадрата)
- Ответ: периметр квадрата равен 28 дм.
Задача 14
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
- 1) 4 ∙ 2 = 8 (длина окна)
- 2) 4 ∙ 8 = 32
- Ответ: площадь окна равна 32 м².
Задача 15
Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
- 1) 54 ∙ 48 = 2592 (площадь участка земли)
- 2) 2592 : 9 = 288 (1/9 площади)
- 4) 2592 – 1440 = 1152
- Ответ: капустой засадили 1152 м².

Простые задачи
- Простые задачи на движение
Составные задачи
- Задачи на встречное движение
- Задачи на движение в одном направлении
- Задачи на противоположное движение
- Задачи на нахождение неизвестного по двум разностям
- Задачи на нахождение числа по доле и доли по числу
- Задачи на нахождение площади
- Задачи на сложение и вычитание многозначных чисел
- Задачи на умножение и деление многозначных чисел
- Задачи на приведение к единице и пропорциональное деление
- Задачи на определение цены, количества, стоимости
Как найти площадь прямоугольника пример. Как посчитать площадь
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
- Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны.
 А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
- Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
- Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два.
 Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Что такое площадь и что такое прямоугольник
Площадь – это такая геометрическая величина, с помощью которой можно определить размер какой-либо поверхности геометрической фигуры.
На протяжении многих веков так повелось, что вычисление площади называли квадратурой. То есть, чтобы узнать площадь несложных геометрических фигур, достаточно было подсчитать количество единичных квадратов, которыми условно были покрыты фигуры. А фигуру, которая имела площадь, называли квадрируемой.
А фигуру, которая имела площадь, называли квадрируемой.
Поэтому, можно подвести итог, что площадь – это такая величина, которая показывает нам размер части плоскости, соединенной между собой отрезками.
Прямоугольник – это такой четырехугольник, у которого все углы прямые. То есть, четырехстороннюю фигуру, которая имеет четыре прямых угла и ее противоположные стороны равны, называют прямоугольником.
Как найти площадь прямоугольника
Самый простой способ нахождения площади прямоугольника – взять прозрачную бумагу, например кальку, или клеенку и расчертить ее на равные квадратики по 1 см, а потом приложить к изображению прямоугольника. Количество заполненных квадратиков и будет площадью в сантиметрах квадратных. Например, на рисунке видно, что прямоугольник попадает в 12 квадратов, значит, его площадь равна – 12 кв. см.
Но для нахождения площади больших объектов, например квартиры, необходим более универсальный способ, поэтому была доказана формула, чтобы найди площадь прямоугольника необходимо умножить его длину на ширину.
А теперь давайте попробуем записать правило нахождения площади прямоугольника в виде формулы. Обозначим площадь нашей фигуры буквой S, буква а – будет обозначать его длину, а буква b – ширину.
В итоге получаем вот такую формулу:
S = а * b.
Если наложить эту формулу на рисунок прямоугольника выше, то мы получим те же 12 кв.см, т.к. а = 4 см, b = 3 см, а S = 4 * 3 = 12 кв.см.
Если взять две идентичные фигуры, и наложить их одну на другую, то они совпадут, а будут называться равными. У таких равных фигур будут также равны их площади и периметры.
Зачем уметь находить площадь
Во-первых, если вы знаете, как найти площадь какой-либо фигуры, то с помощью ее формулы вы без проблем сможете решать любые задачи по геометрии и тригонометрии.
Во-вторых, научившись находить площадь прямоугольника, вы сначала сможете решать простые задачки, а со временем перейдете к решению более сложных, и научитесь находить площади фигур, которые вписаны в прямоугольник или около него.
В-третьих, зная такую простую формулу, как S = а * b, вы получаете возможность без проблем решать любые простые бытовые задачи (например, находить S квартиры или дома), а со временем и сможете применить их к решению сложных архитектурных проектов.
То есть, если совсем упростить формулу нахождения площади, то она будет выглядеть так:
П = Д х Ш,
Что обозначает П – это искомая площадь, Д – это ее длина, Ш – обозначает ее ширину, а х – является знаком умножения.
А известно ли вам, что площадь любого многоугольника можно условно разбить на определенное количество квадратных блоков, которые находятся внутри этого многоугольника? Какая разница между площадью и периметром
Давайте на примере попробуем понять разницу между периметром и площадью. Например, наша школа находится на участке, который огражден забором – суммарная длина этого забора будет периметром, а то пространство, которое находится внутри ограждения и является площадью.
Единицы измерения площади
Если периметр одномерный измеряется в линейных единицах, которыми являются дюймы, футы и метры, то S относится к двумерным исчислениям и имеет свою длину и ширину.
И измеряется S в квадратных единицах, таких, как:
Один квадратный миллиметр, где S квадрата имеет сторону, равную одному миллиметру;
Квадратный сантиметр, имеет S такого квадрата, у которого сторона равна одному сантиметру;
Квадратный дециметр равен S этого квадрата со стороной в один дециметр;
Квадратный метр имеет S квадрата, сторона которого равна одному метру;
И наконец, квадратный километр имеет S квадрата, сторона которого равна одному километру.
Для измерения площадей больших участков на поверхности Земли используют такие единицы, как:
Один ар или сотка – если S квадрата имеет сторону десять метров;
Один гектар равен S квадрата, у которого сторона имеет сто метров.
Задачи и упражнения
А теперь давайте рассмотрим несколько примеров.
На рисунке 62 нарисована фигура, которая имеет восемь квадратов и каждая сторона этих квадратов равна одному сантиметру. Поэтому S такого квадрата будет квадратный сантиметр.
Если записать, то это будет выглядеть так:
1 см2. А S все этой фигуры, состоящей из восьми квадратов, будет равняться 8 кв.см.
А S все этой фигуры, состоящей из восьми квадратов, будет равняться 8 кв.см.
Если взять какую-нибудь фигуру и разбить ее на «р» квадратов со стороной, равной одному сантиметру, то ее площадь будет равна:
Р см2.
Давайте рассмотрим прямоугольник, изображений на рисунке 63. Этот прямоугольник состоит из трех полос, а каждая такая полоска разбита на пять равных квадратов, имеющих сторону в 1 см.
Попробуем найти его площадь. И так берем пять квадратов, и умножаем на три полоски и получаем площадь равную 15 кв.см.:
Рассмотрим следующий пример. На рисунке 64 изображен прямоугольник ABCD, ломаной линией KLMN он разбит на две части. Первая его часть равна площади 12 см2, а вторая имеет площадь 9 см2. Теперь давайте найдем площадь всего прямоугольника:
Итак, берем три и умножаем на семь и получаем 21 кв.см:
3 7 = 21 кв.см. При этом 21 = 12 + 9.
И приходим к выводу, что площадь всей нашей фигуры равна сумме площадей ее отдельных частей.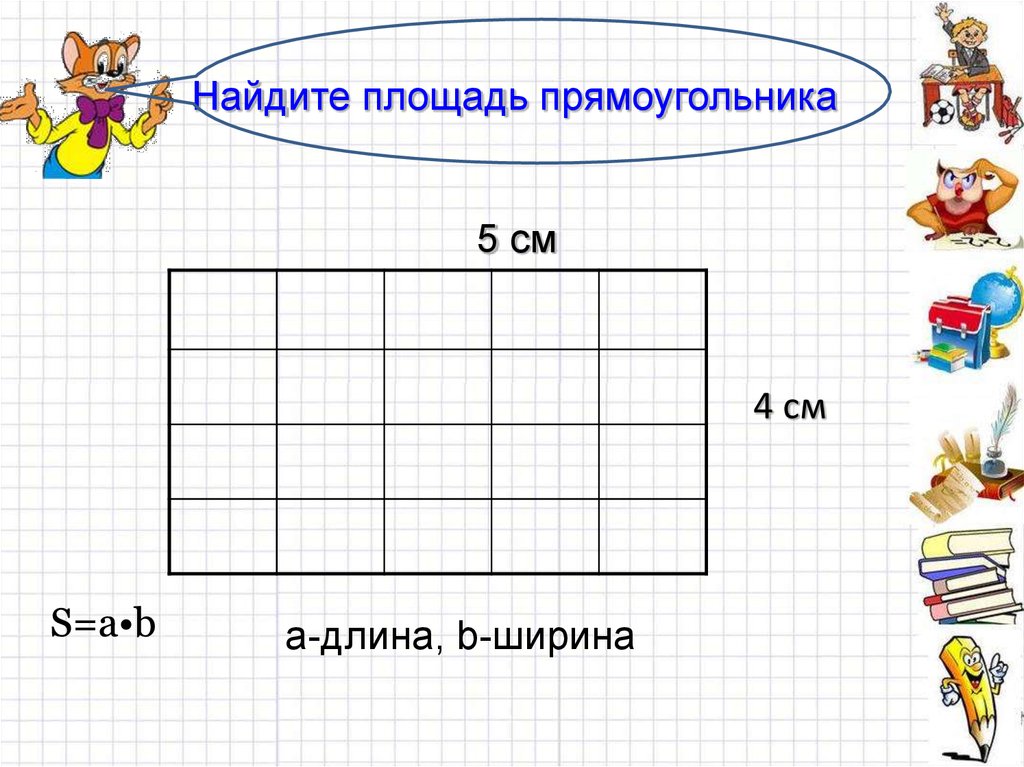
Рассмотрим еще один пример. И так на рисунке 65 изображен прямоугольник, который с помощью отрезка АС разбит на два равных треугольника ABC и ADC
А так, как нам уже известно, что квадрат – это такой же прямоугольник, только имеющий равные стороны, то площадь каждого треугольника будет равняться половине площади всего прямоугольника.
Представим, что сторона квадрата равна а, то:
S = a a = a2.
Делаем вывод, что формула площади квадрата будет иметь такой вид:
А запись a2 называется квадратом числа а.
И так, если сторона нашего квадрата равна четырем сантиметрам, то его площадь будет:
4 4, то есть 4 * 2 = 16 кв.см.
Вопросы и задания
Найдите площадь фигуры, которая разбита на шестнадцать квадратов, сторона которых равна одному сантиметру.
Вспомните формулу прямоугольника и запишите ее.
Какие измерения нужно произвести, чтобы узнать площадь прямоугольника?
Дайте определение равным фигурам.
Могут ли иметь равные фигуры различные площади? А периметры?
Если вам известны площади отдельных частей фигуры, как узнать ее общую площадь?
Сформулируйте и запишите, чему равняется площадь квадрата.
Историческая справка
А известно ли вам, что древние люди в Вавилоне умели рассчитать площадь прямоугольника. Так же древние египтяне делали расчеты различных фигур, но так как точных формул они не знали, то вычисления имели небольшие погрешности.
В своей книге «Начала» знаменитый древнегреческий математик Евклид, описывает различные способы вычисления площадей разных геометрических фигур.
Инструкция
Чтобы найти длину стороны прямоугольника, если известна ширина и площадь , разделите числовое значение площади на числовое значение ширины. То есть воспользуйтесь формулой:Д = П / Ш, где:Д – длина стороны прямоугольника,
Ш – ширина прямоугольника,
П – его площадь .Например, если площадь прямоугольника равна 20 см², а его ширина – 5 см, то длина его стороны будет: 20 / 5 = 4 см.
Перед началом вычислений переведите ширину и площадь прямоугольника в одну систему измерений. То есть, площадь должна выражаться в соответствующих ширине квадратных единицах измерения. При этом, длина получится в тех же единицах, что и ширина . Так, если ширина задана в метрах, то площадь необходимо в . Особенно актуален такой при измерении земельных участков, где площадь обычно задана в гектарах, арах и «сотках».
При этом, длина получится в тех же единицах, что и ширина . Так, если ширина задана в метрах, то площадь необходимо в . Особенно актуален такой при измерении земельных участков, где площадь обычно задана в гектарах, арах и «сотках».
Например, пусть площадь дачного участка равняется шести соткам, а его ширина – 30 метров. Требуется найти длину участка.
Так как «соткой» 100 , то площадь «стандартных» шести можно записать как 600 м². Отсюда длину земельного участка можно найти разделив 600 на 30. Получается – 20 метров.
Иногда заданы площадь и ширина фигуры, имеющей не прямоугольную, а произвольную форму. При этом, также требуется найти ее длину . Как правило, в это случае подразумеваются габаритные фигуры, то есть параметры прямоугольника, в который эту фигуру можно заключить.
Если большая точность вычислений не требуется, то воспользуйтесь вышеприведенной формулой (Д = П / Ш). Однако, значение длины при этом получится заниженным. Чтобы получить более точное значение длины фигуры, оцените насколько полно фигура заполняет свой габаритный прямоугольник и разделите полученную длину на коэффициент заполнения.
Однако, значение длины при этом получится заниженным. Чтобы получить более точное значение длины фигуры, оцените насколько полно фигура заполняет свой габаритный прямоугольник и разделите полученную длину на коэффициент заполнения.
Источники:
- Какова длина прямоугольника, если известна его ширина
Каждая геометрическая фигура обладает определенными характеристиками, которые, в свою очередь, связаны между собой. Поэтому для того, чтобы найти площадь прямоугольника, нужно знать, какова длина его сторон.
Прямоугольник — одна из самых распространенных геометрических фигур. Он представляет собой четырехугольник, все углы которого равны между собой и составляют по 90 градусов. Эта характеристика, в свою очередь, влечет за собой определенные последствия в отношении других параметров рассматриваемой фигуры.
Во-первых, его стороны, располагающиеся друг напротив друга, будут параллельны. Во-вторых, эти стороны будут попарно равны между собой по длине. Эти характеристики оказываются очень важными для исчисления других его параметров, таких как площадь.
Эти характеристики оказываются очень важными для исчисления других его параметров, таких как площадь.
Порядок вычисления площади прямоугольника
Для того чтобы вычислить , необходимо иметь информацию о том, какова длина его сторон. Следует помнить, что стороны прямоугольника не равны по этому показателю: прямоугольник, все стороны которого равны между собой по длине, представляет собой другую геометрическую фигуру, которая носит название квадрата.
Поэтому для обозначения различающихся сторон прямоугольника приняты особые обозначения: так, сторону с большой протяженностью обычно называют длиной фигуры, а сторону с меньшей протяженностью — его шириной. При этом каждый прямоугольник в силу его свойств, описанных выше, имеет две длины и две ширины.
Собственно алгоритм вычисления площади этой фигуры достаточно прост: необходимо лишь его одну длину умножить на одну его ширину. Полученное произведение будет представлять собой площадь прямоугольника.
Пример вычисления
Предположим, есть прямоугольник, одна сторона которого составляет 5 сантиметров, а другая — 8 сантиметров. Таким образом, согласно данному выше определению, длина этой фигуры, измеряемая как протяженностью большей стороны, будет равна 8 сантиметрам, а ширина — 5 сантиметрам.
Для нахождения площади фигуры необходимо ее ширину умножить на длину: таким образом, площадь рассматриваемого прямоугольника составит 40 квадратных сантиметров. Обратите внимание, что для осуществления вычислений оба используемых параметра должны измеряться в одинаковых единицах, например
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем жизненном пути встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90°. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в старших классах, приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади прямоугольного треугольника. Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать радиус окружности. Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Для использования данного способа необходимо знать радиус окружности. Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами.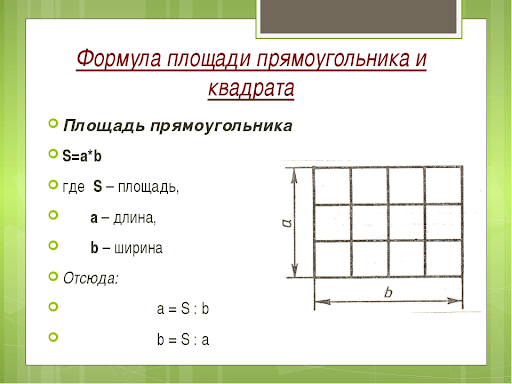 Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Прямоугольник – это частный случай четырехугольника. Это значит, что у прямоугольника четыре стороны. Его противоположные стороны равны: так например, если одна из его сторон равна 10 см, то противоположная ей будет так же равны 10 см. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.
Как узнать площадь прямоугольника по двум сторонам
Для того чтобы найти площадь прямоугольника, надо умножить его длину на ширину: Площадь = Длина × Ширина. В случае, указанном ниже: Площадь = AB × BC.
Как узнать площадь прямоугольника по стороне и длине диагонали
В некоторых задачах необходимо найти площадь прямоугольника, используя длину диагонали и одну из сторон. 2 × sin(острого угла между диагоналями)/2.
2 × sin(острого угла между диагоналями)/2.
Площади фигур (плоских и объемных)
Сначала мы рассмотрим площади плоских фигур.
Слышал ты что-нибудь про формулу Пика? Когда ее можно применять, а когда нельзя?
Сколько ты знаешь способов нахождения площади фигур на клетчатой бумаге? А их на самом деле три! И хотя задачу по нахождению площади фигур на клетчатой бумаге убрали из ЕГЭ, сам навык очень полезен для понимания планиметрии!
Во второй части мы рассмотрим как находить площади объемных фигур (призмы и пирамиды)
ПЛОЩАДИ ПЛОСКИХ ФИГУР
Способы нахождения площади фигур на клетчатой бумаге:
Способ 1. Считай клетки и применяй формулы
Удобен для стандартных фигур: треугольника, трапеции и т.д.
- Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
- Подставить найденные значения в уравнение площади.

Способ 2. Дострой до прямоугольника и вычти лишнее
Очень удобен для сложных фигур, но и для простых неплох
- Достроить искомую фигуру до прямоугольника;
- Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
- Из площади прямоугольника вычесть сумму площадей всех лишних фигур.
Способ 3. Формула Пика
Работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.
- Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.
Подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
В примере на рисунке получилось \( Г = 22\) на границе и \( В = 32\) внутри.
Формула Пика. Делим границу пополам, прибавляем внутренности и вычитаем 1:\( S = Г/2 + В – 1 \)
В примере на рисунке:
\( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.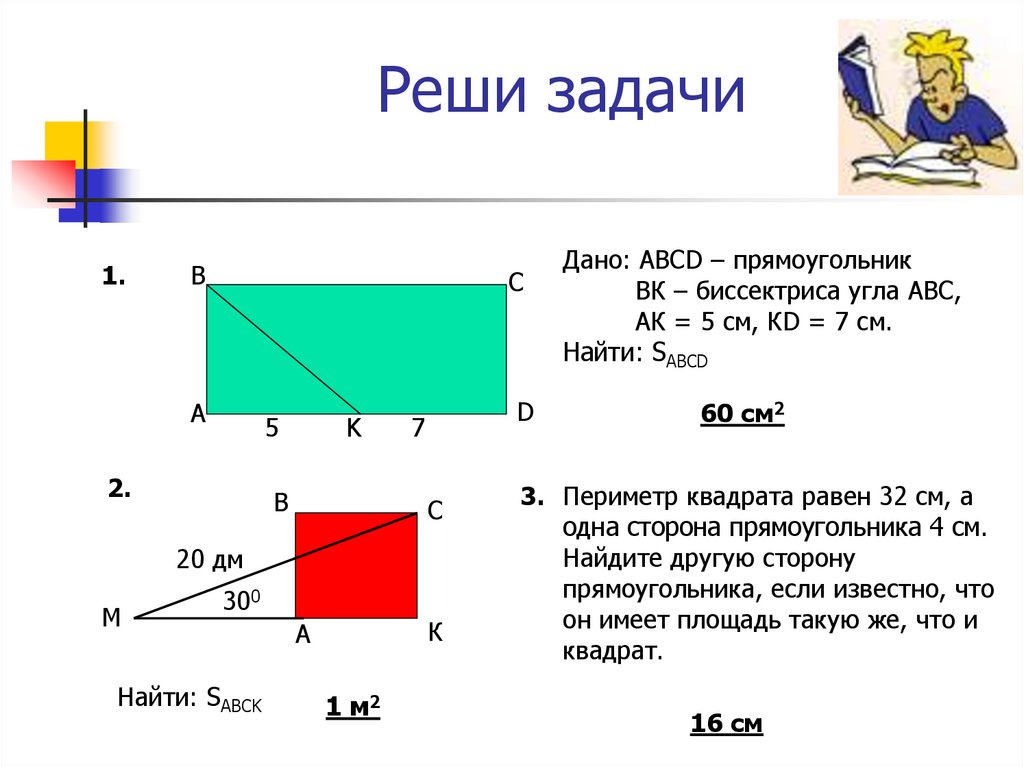 \)
\)
Удобен для стандартных фигур: треугольника, трапеции и т.д.
- Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
- Подставить найденные значения в уравнение площади.
Пусть нужно найти площадь трапеции, построенной на листе в клетку.
Просто считаем клеточки и видим, что в нашем случае \( \displaystyle a=17\), \( \displaystyle b=6\) и \( \displaystyle h=6\). Подставляем в формулу:
\( \displaystyle S=\frac{a+b}{2}\cdot h=\frac{17+6}{2}\cdot 6=69\)
Но бывает, что не так-то просто рассчитать, сколько клеток в нужном отрезке. Вот смотри, треугольник:
Вроде бы даже прямоугольный и \( \displaystyle S=\frac{1}{2}\cdot ab\), но чему тут равно \( \displaystyle a\), и чему равно \( \displaystyle b\)?
Как узнать?
Найдем \( \displaystyle a\) по теореме Пифагора из \( \displaystyle \Delta ADC\), а \( \displaystyle b\) по теореме Пифагора из \( \displaystyle \Delta BCE\).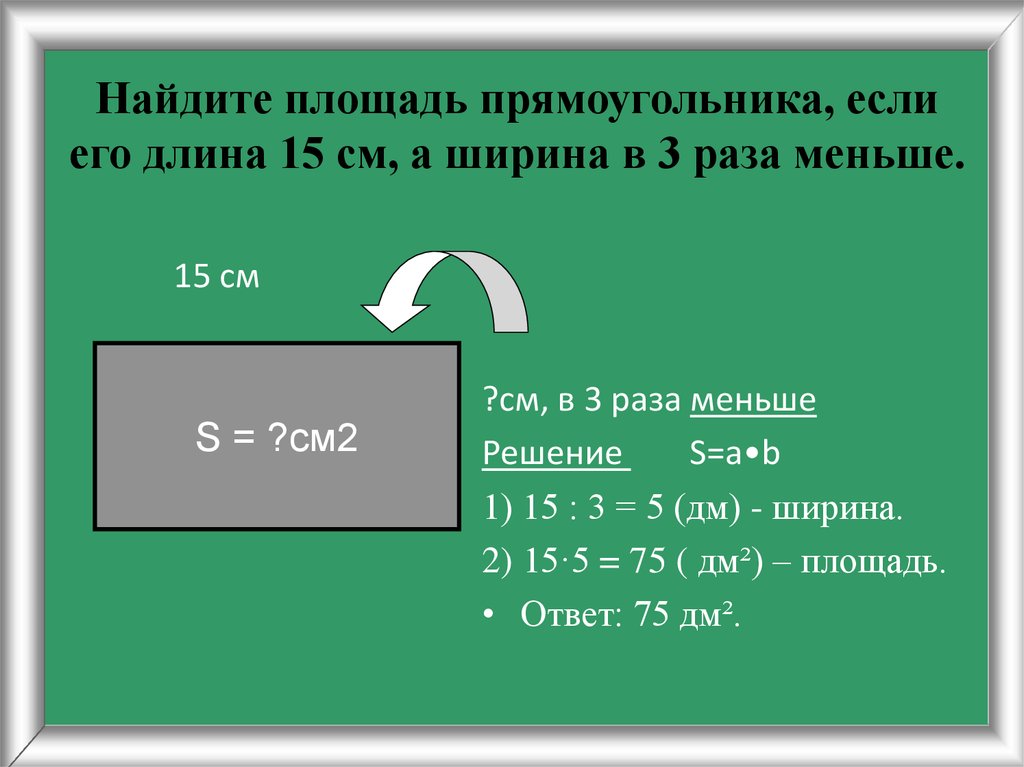 {2}}=13\).
{2}}=13\).
\( \displaystyle b=\sqrt{13}\)
Подставляем в формулу:
\( \displaystyle S=\frac{1}{2}\cdot ab=\frac{1}{2}\cdot 2\sqrt{13}\cdot \sqrt{13}=13\).
Способ 2. Дострой до прямоугольника и вычти лишнееОчень удобен для сложных фигур, но и для простых неплох
- Достроить искомую фигуру до прямоугольника;
- Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
- Из площади прямоугольника вычесть сумму площадей всех лишних фигур.
Давай посчитаем площадь того же треугольника вторым способом.
Нужно окружить нашу фигуру прямоугольником. Вот так:
Получился один (нужный) треугольник внутри и целых три ненужных треугольника снаружи. Но зато площади этих ненужных треугольников легко считаются на листе в клетку!
Вот мы их посчитаем, а потом просто вычтем из целого прямоугольника:
\( \displaystyle {{S}_{прямоугольника}}=6\cdot 7=42\)
\( \displaystyle {{S}_{1}}=\frac{1}{2}\cdot 6\cdot 4=12\)
\( \displaystyle {{S}_{2}}=\frac{1}{2}\cdot 7\cdot 4=14\)
\( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 3\cdot 2=3\)
\( \displaystyle \Rightarrow S=42-12-14-3=13\)
Почему бы просто не считать клеточки?
Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать.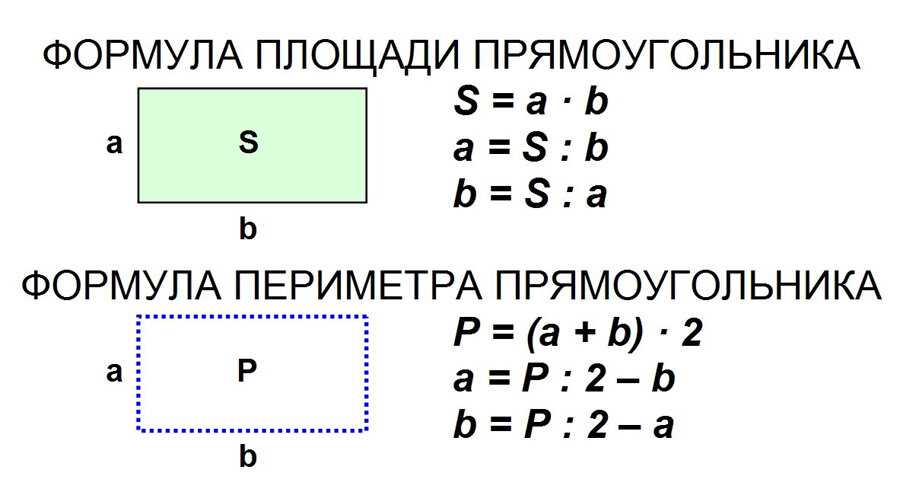 Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.
Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.
Вот, например, трапеция:
Посчитаем клеточки: их всего 46, верно?
Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе \( 36+\frac{10}{2} = 41\)
Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…
Как всё это учитывать?
Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.
А жёлтые сколько занимают? Постарайтесь ответить сами.
Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.
Итак, 2 жёлтых куска = 1 клетка.
Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки.
Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это \( 36+\frac{6}{2}=39\) клетки.
Итого клеток: \( 1 + 2 + 39 = 42\).
Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.
Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).
Способ 3. Формула ПикаСуществует довольно удобная формула, которая использует клеточки для вычисления площади. А то, что мы только что проделали, – очень полезное упражнение, которое поможет эту формулу понять.
Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.
Теперь вместо клеточек или их частей подсчитаем, сколько узлов попадает в нашу фигуру.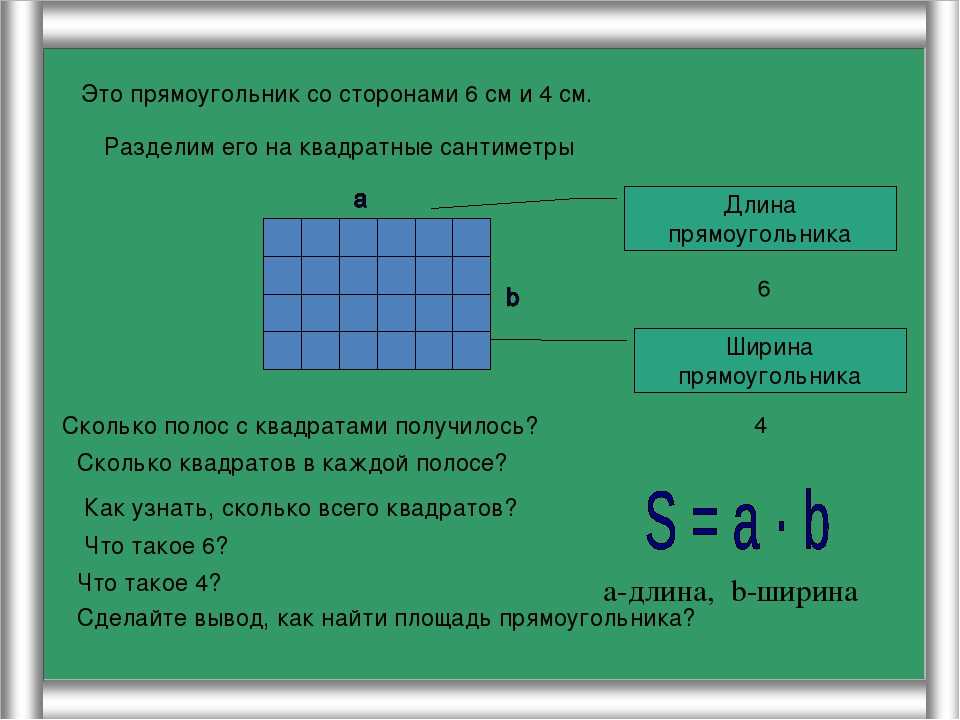 Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
Сколько насчитали?
У меня получилось \( Г = 22\) на границе и \( В = 32\) внутри.
Ну а теперь сама формула:
Делим границу пополам, прибавляем внутренности и вычитаем 1:
\( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.\)
Называется она формулой Пика, поскольку доказал её математик Георг Пик 120 лет назад (да, она не специально для ЕГЭ была придумана, но очень нам помогает) 🙂
Как запомнить формулу Пика
Всё, что внутри, берём целиком (клетки внутри фигуры целые).
Граница режет клетки надвое, поэтому берём половину узлов границы.
Минус 1 – это надо просто запомнить. Очень легко себя проверить на квадрате 1×1. Его площадь равна 1. Сколько там точек на границе? \( Г = 4.\) А сколько внутри? \( В = 0\) (нисколько)
Границу делим пополам, получаем 2. Прибавляем внутренности (+0) – ничего не поменялось.
Прибавляем внутренности (+0) – ничего не поменялось.
Очевидно, что осталось вычесть 1, чтобы получить 1.
Проверьте эту формулу на других простых фигурах, чтобы убедиться и закрепить.
Вычислите площадь простых фигур тремя способами
Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.
Вычислите площадь произвольных фигур по формуле Пика
Вычислите самостоятельно площади фигур с помощью формулы Пика:
Посчитайте площадь корабля и котика по формуле Пика
Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!
Фигуры с отверстиями — посчитайте площади двумя способами
Ну и напоследок фигуры с «дырками». Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?
Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?
Проверим на простом примере: это квадрат \( 4\times 4\), и в нём вырезан прямоугольник \( 1\times 2\), значит, его площадь \( 16-2=14\).
А теперь по точкам. На границах (включая внутренние) \( Г = 22\). Внутри \( В = 3\). Тогда площадь по формуле Пика
\( S = \frac{22}{2} + 3 -1 = 13.\)
Хм, близко, но не совпало. Может, я где-то ошибся? Давай ещё одну фигуру, для верности.
Сосчитай сам и проверь.
Что получилось?
У меня снова на 1 меньше.
Так может быть просто формулу немного «подкрутить»? Нет!
Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.
Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.
Когда формулу Пика применять нельзя?
Естественно, эта формула не работает для окружностей и любых других фигур с «кривыми» границами.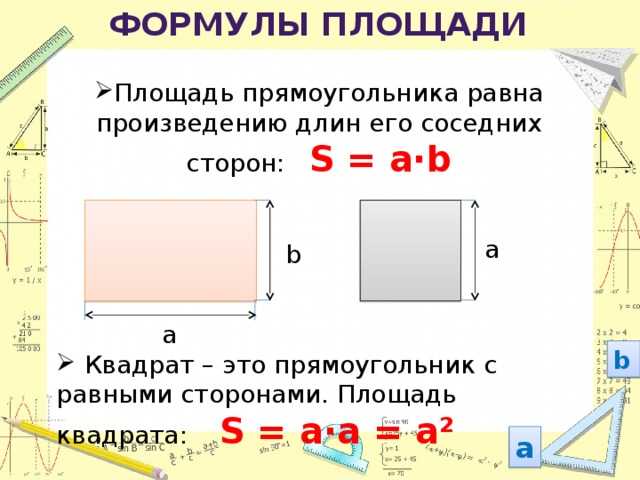
Также она не сработает, если хотя бы одна из вершин не попадает на узел, например, вот для такой, как на рисунке.
Почему я уверен, что не сработает? Ведь можно взять и не учитывать эту вершину, раз она не в узле. То есть
\( Г = 10, В = 2, S = \frac{10}{2} + 2 – 1 = 6.\)
А очень просто: я возьму и «отрежу» эту вершину. Тогда будет не треугольник, а трапеция, и площадь, очевидно, станет меньше на тот отрезанный кусочек.
Но по формуле она останется такой же, ведь количество узлов не изменилось ни на границе, ни внутри. То есть мы получим, что площадь уменьшенного треугольника равна площади целого, чего, конечно же, не может быть.
Итак, формула Пика работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.
Какой способ лучше?
Второй и третий способы универсальные. Они помогут посчитать площадь даже самых замысловатых фигур. Вернемся еще раз ко второму способу.
Вернемся еще раз ко второму способу.
Вот смотри, нужно посчитать площадь такой фигуры:
Окружаем ее прямоугольником и снова получаем одну нужную, но сложную площадь и много ненужных, но простых.
А теперь чтобы найти площадь \( \displaystyle S\) просто находим площадь прямоугольника и вычитаем из него оставшуюся площадь фигур на клетчатой бумаге \( \displaystyle {{S}_{1}}+{{S}_{2}}+{{S}_{3}}+{{S}_{4}}\).
\( \displaystyle {{S}_{прямоугольника}}=6\cdot 11=66\)
\( \displaystyle {{S}_{1}}=\frac{1}{2}\cdot 6\cdot 4=12\)
\( \displaystyle {{S}_{2}}=\frac{1}{2}\cdot a\cdot h=\frac{1}{2}\cdot 5\cdot 4=10\) (обрати внимание, \( \displaystyle {{S}_{2}}\) площадь НЕ прямоугольного треугольника, но все равно легко считается по основной формуле).
\( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 5\cdot 2=5\)
\( \displaystyle {{S}_{4}}=\frac{1}{2}\cdot 1\cdot 11=5,5\).
Значит, \( \displaystyle S={{S}_{прямоугольника}}-{{S}_{1}}-{{S}_{2}}-{{S}_{3}}-{{S}_{4}}\).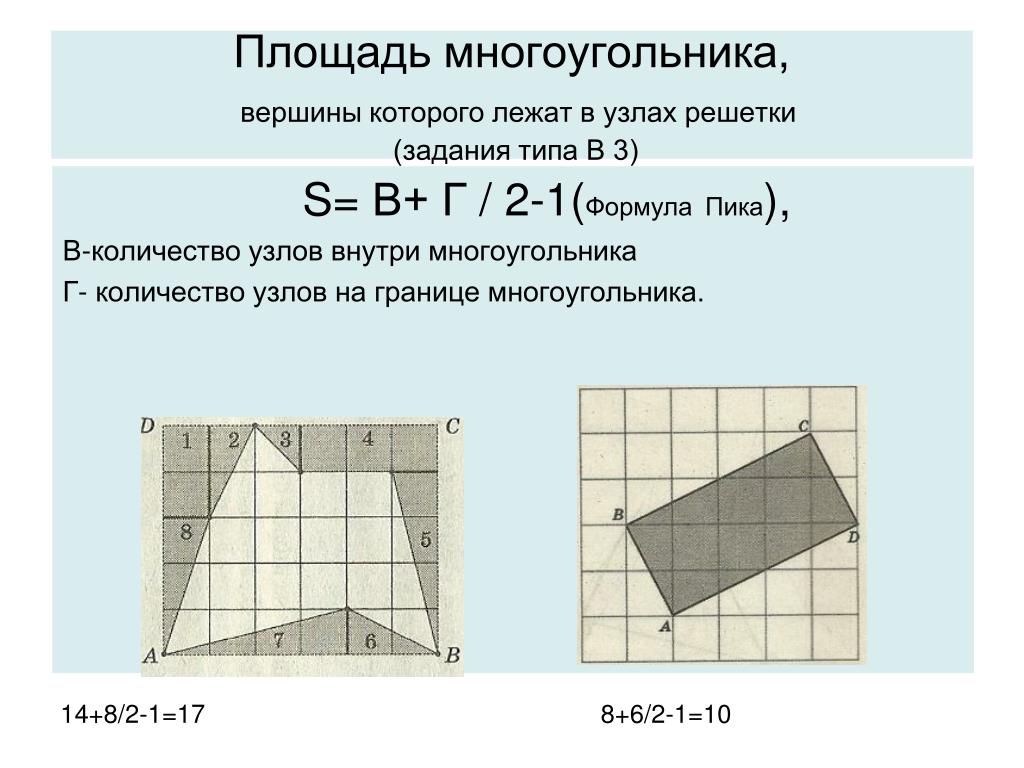
\( \displaystyle S=66-12-10-5-5,5=33,5\)
Вот и ответ: \( \displaystyle S=33,5\).Ну как тебе этот способ?
Вот смотри. С одной стороны, когда фигура занимает много клеточек, их замучаешься считать и можно ошибиться.
С другой стороны, когда мы дорисуем до прямоугольника, нужно считать много площадей.
Поэтому использование того или иного способа зависит лишь от конкретной задачи.
ПЛОЩАДИ ОБЪЕМНЫХ ФИГУР
Площадь поверхности призмы
Есть ли общая формула? Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.
Площадь полной поверхности призмы – это сумма площадей всех граней.
\( \displaystyle {{S}_{полн. пов.\ \ }}={{S}_{боков.пов.\ \ }}+2\cdot {{S}_{основания\ \ }}\)
Формулу можно написать для прямой призмы:
\( \displaystyle {{\text{S}}_{боков. {2}}\).
{2}}\).
Площадь поверхности пирамиды
Для пирамиды тоже действует общее правило:
Площадь полной поверхности пирамиды – это сумма площадей всех граней.\( \displaystyle {{S}_{полн. пов.\ \ }}={{S}_{боков.пов.\ \ }}+{{S}_{основания\ \ }}\)
Теперь давай посчитаем площадь поверхности самых популярных пирамид.
Площадь поверхности правильной треугольной пирамиды
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Нужно найти \( \displaystyle {{S}_{осн}}\) и \( \displaystyle {{S}_{ASB}}\).
И тогда
\( \displaystyle {{S}_{полн. пов.\ \ }}=3{{\text{S}}_{ASB}}+{{\text{S}}_{\text{осн}.}}\)
Вспомним теперь, что
\( \displaystyle {{S}_{осн}}\) — это площадь правильного треугольника \( \displaystyle ABC\).
И еще вспомним, как искать эту площадь.
Используем формулу площади:
\( \displaystyle S=\frac{1}{2}ab\cdot \sin \gamma \).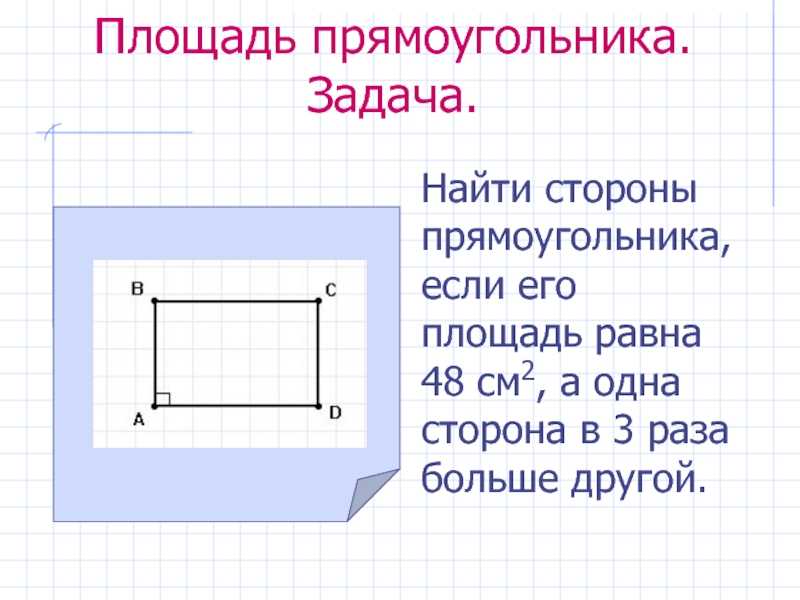 2}{4}}\)
2}{4}}\)
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
Этот вебинар посвящен заданию №3 из ЕГЭ на нахождение площади фигур, длин отрезков и т.д на клетчатой бумаге.
И хотя эту задачу убрали из ЕГЭ в 2021 году, сам навык очень полезен для того, чтобы начать учить геометрию, для понимания планиметрии!
Ну и просто этот вебинар легкий и классный! Послушайте его и получите удовольствие!
ЕГЭ №3. Площадь фигур на клетчатой бумаге
Площадь трапеции abcd. Нахождение площади трапеции. Формула герона для площади трапеции.
- Альфашкола
- Статьи
- Площади трапеции
Как найти площадь трапеции?
Складываем основания трапеции, делим сумму на два и умножаем все это на высоту, проведенную к большему основанию.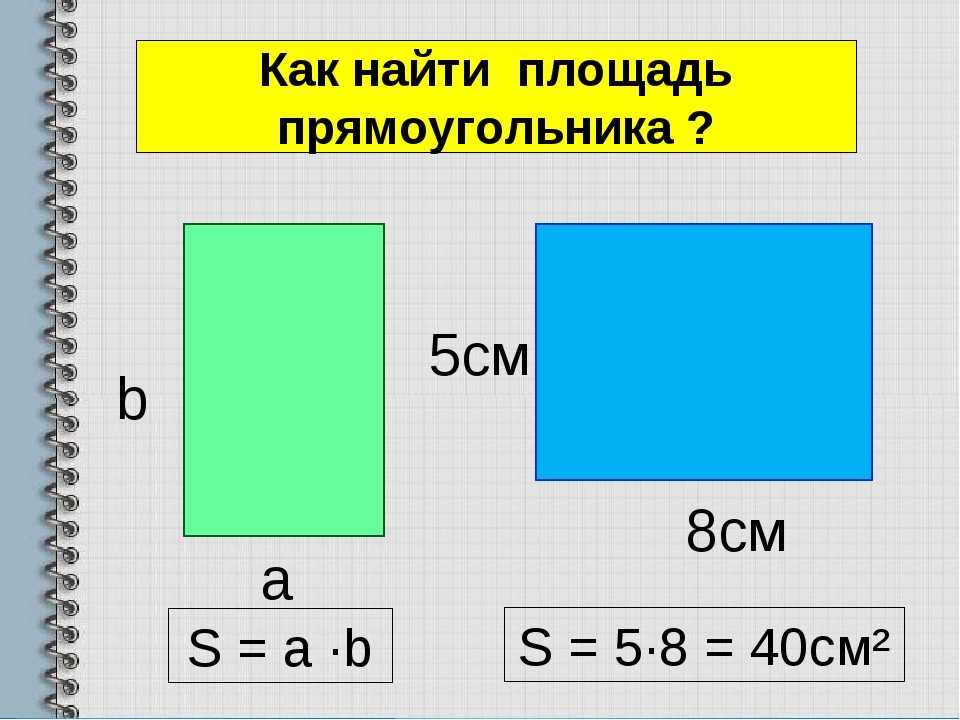
\(S=\frac{a+b}{2}h\)
Первое основание трапеции a:
Второе основание трапеции b:
Высота трапеции:
Также мы можем вычислить площадь трапеции зная все стороны трапеции (формула Герона):
\(s=\frac{a+b}{|a-b|}\sqrt{(p-a)(p-b)(p-a-c)(p-a-d)}\)
где: \(p=\frac{a+b+c+d}{2}\)
Первая сторона трапеции a:
Вторая сторона трапеции b:
Третья сторона трапеции c:
Четвертая сторона трапеции d:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Алесандр Викторович Рудаков
Репетитор по математике
Стаж (лет)
Образование:
Омский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5 классов и по информатике для 7-9 классов, подготовка к ОГЭ. Самые сложные темы по математике на моих занятиях станут для вас очень простыми. Подготовлю вас к ВПР по математике, к ОГЭ по информатике. Пропагандирую сотрудничество на равных, дружественная атмосфера на занятиях. Индивидуальный подход к каждому ребенку.
Самые сложные темы по математике на моих занятиях станут для вас очень простыми. Подготовлю вас к ВПР по математике, к ОГЭ по информатике. Пропагандирую сотрудничество на равных, дружественная атмосфера на занятиях. Индивидуальный подход к каждому ребенку.
Виктор Дмитриевич Ильин
Репетитор по математике
Стаж (лет)
Образование:
ГОУ ВО Луганский государственный университет имени Владимира Даля, Кафедра теории и практики перевода германских и романских языков факультета филологии и массовых коммуникаций
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по английскому языку для 1- 11 классов. Подготовка к ОГЭ, ЕГЭ, ВПР.
Индивидуальный подход к каждому ученику, в зависимости от его уровня владения иностранным языком. Обучение возможно как по Вами желаемой программе, так и по выбранной мною, в любое удобное для Вас время.
Дошкольники: Подготовка к школе: развитие интереса к языку, алфавит, звуки, буквы и транскрипции.
Начальные классы: Прохождение школьной программы с её опережением.
Средние классы: Написание «топиков», грамматика, перевод, подготовка к контрольным и самостоятельным.
Старшие классы: Подготовка к экзаменам по иностранному языку, аудирование, грамматика, пересказ и т.п.
Занятия со взрослыми: Практика разговорных навыков, восстановление пробелов в обучении, техника перевода.
О себе: Сотрудник кафедры лингвистики и международных отношений (кафедра иностранных языков и практики перевода) высшего учебного заведения. Окончил гимназию иностранных языков. Опыт в работе с учениками разных возрастов и разных уровней знания языка.
Подготовка к ОГЭ, ЕГЭ, ВПР.
Индивидуальный подход к каждому ученику, в зависимости от его уровня владения иностранным языком. Обучение возможно как по Вами желаемой программе, так и по выбранной мною, в любое удобное для Вас время.
Дошкольники: Подготовка к школе: развитие интереса к языку, алфавит, звуки, буквы и транскрипции.
Начальные классы: Прохождение школьной программы с её опережением.
Средние классы: Написание «топиков», грамматика, перевод, подготовка к контрольным и самостоятельным.
Старшие классы: Подготовка к экзаменам по иностранному языку, аудирование, грамматика, пересказ и т.п.
Занятия со взрослыми: Практика разговорных навыков, восстановление пробелов в обучении, техника перевода.
О себе: Сотрудник кафедры лингвистики и международных отношений (кафедра иностранных языков и практики перевода) высшего учебного заведения. Окончил гимназию иностранных языков. Опыт в работе с учениками разных возрастов и разных уровней знания языка.
Александр Ринатович Набиуллин
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии для 7-11 классов. Подготовка к ОГЭ, ЕГЭ. «Химик — он не бог, но всё умеет». Старый полушутливый девиз из студенчества.
Химия — это практически всё, что нас окружает. Понимание её сути позволяет очень многое: различать полезные добавки в пище, бесполезные и небезопасные, понимать роль удобрений для растений и роль лекарств для человека. Кроме того, это ещё и очень интересно. :)
Понимание химии — универсальный ключ к знаниям в этой области. Это позволяет решать любые практические и теоретические задачи, от школьного до олимпиадного уровня.
Подготовка к ОГЭ, ЕГЭ. «Химик — он не бог, но всё умеет». Старый полушутливый девиз из студенчества.
Химия — это практически всё, что нас окружает. Понимание её сути позволяет очень многое: различать полезные добавки в пище, бесполезные и небезопасные, понимать роль удобрений для растений и роль лекарств для человека. Кроме того, это ещё и очень интересно. :)
Понимание химии — универсальный ключ к знаниям в этой области. Это позволяет решать любые практические и теоретические задачи, от школьного до олимпиадного уровня.
Похожие статьи
- Математические факты о Чичен-Ица в Мексике
- Площадь поверхности конуса
- Положительное и отрицательное направление угла
- Финансовый Университет: факультет Бизнес-Информатики
- Определение чисел по их сумме и разности
- Задачи «на части»
- Теорема косинусов
- ЕГЭ по математике, базовый уровень.
 Планиметрия. Равнобедренный треугольник (вариант 1)
Планиметрия. Равнобедренный треугольник (вариант 1)
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Задачи на нахождение периметра и площади
Примеры решения задач разной сложности на нахождение периметра и площади
Условные обозначения и формулы
- a — длина
- b — ширина
- P — периметр
- S — площадь
Квадрат → определение
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
Прямоугольник → определение
P = a + b + a + b; P = 2a + 2b; P = (a + b) · 2 – периметр прямоугольника
S = a · b — площадь прямоугольника
Задачи
Треугольник → определение
S = ½ · a · h – площадь треугольника
P = a + b + c – периметр треугольника
Задачи
Круг → определение
P = πD; P = 2πR — длина окружности
S = πR2; S = πD2 : 4 – площадь круга
Задачи
30 задач – от простого к сложному
Задача №1
Найди периметр квадрата со стороной 8 см.
Решение:
8 · 4 = 32 (см)Ответ: периметр квадрата 32 см.
Задача №2
Найди периметр квадрата со стороной 16 см.
Решение:
16 · 4 = 64 (см)Ответ: периметр квадрата 64 см.
Задача №3
Периметр квадрата 16 см. Найди его сторону.
Решение:
16 : 4 = 4 (см)Ответ: сторона квадрата 4 см.
Задача №4
Найди периметр прямоугольника со сторонами 9 и 6 см.
Решение:
(9 + 6) · 2 = 30 (см)Ответ: периметр прямоугольника 30 см.
Задача №5
Найди периметр прямоугольника со сторонами 7 и 8 см.
Решение:
(7 + 8) · 2 = 30 (см)Ответ: периметр прямоугольника 30 см.
Задача №6
Найди длину прямоугольника, если его ширина 7 см, а периметр равен 40 см.
Решение:
Вариант Ⅰ
У прямоугольника противоположные стороны равны, то есть две равных ширины и две равных длины.
Если одна ширина (сторона) 7 см, то и другая (противоположная) тоже 7 см.
7 + 7 = 14 (см)
Периметр состоит из суммы длин четырёх сторон прямоугольника, сумму двух противоположных сторон мы уже узнали, тогда сумма двух других противоположных сторон (длин) будет равна:
40 — 14 = 26 (см)
Теперь узнаем длину одной стороны:
26 : 2 = 13 (см)Ответ: длина прямоугольника 13 см.
или
Вариант Ⅱ
P = (a + b) · 2 — периметр прямоугольникаили
(a + b) · 2 = P, где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.

Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 — 14
2а = 26
а = 26 : 2
а = 13Ответ: длина прямоугольника 13 см.
Задача №7
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Решение:
Вариант Ⅰ
У прямоугольника противоположные стороны равны, то есть две равных ширины и две равных длины.
Если одна длина (сторона) 10 см, то и другая (противоположная) тоже 10 см.
10 + 10 = 20 (см)
Периметр состоит из суммы длин четырёх сторон прямоугольника, сумму двух противоположных сторон мы уже узнали, тогда сумма двух других противоположных сторон будет равна:
30 — 20 = 10 (см)
Теперь узнаем ширину одной стороны:
10 : 2 = 5 (см)Ответ: ширина прямоугольника 5 см.
или
Вариант Ⅱ
P = (a + b) · 2 — периметр прямоугольникаили
(a + b) · 2 = P, где a — длина = 10 см, b — ширина = ?, P — периметр = 30 см.
Составим уравнение:
(10 + b) · 2 = 30
20 + 2b = 30
2b = 30 — 20
2b = 10
b = 10 : 2
b = 5Ответ: ширина прямоугольника 5 см.
Задача №8
Ширина прямоугольника 14 см. Длина на 5 см больше. Найди его периметр и площадь.
Решение:
14 + 5 = 19 (см)
(19 + 14) · 2 = 66 (см)
19 · 14 = 266 (см²)Ответ: периметр прямоугольника 66 см; площадь прямоугольника 266 см².
Задача №9
Длина прямоугольника 7 см. Ширина на 3 см меньше. Найди его периметр и площадь.
Решение:
7 — 3 = 4 (см)
(7 + 4) · 2 = 22 (см)
7 · 4 = 28 (см²)Ответ: периметр прямоугольника 22 см; площадь прямоугольника 28 см².
Задача №10
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)Ответ: площадь квадрата 36 см².
Задача №11
Периметр квадрата 36 см. Найди его площадь.
Решение:
36 : 4 = 9 (см)
9 · 9 = 81 (см²)Ответ: площадь квадрата 81 см².
Задача №12
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см.
На сколько см² он ошибся?Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)Ответ: он ошибся на 3 см².
Задача №13
Ученику нужно было начертить прямоугольник со сторонами 10 см и 8 см, а он начертил его со сторонами 8 см и 6.

На сколько см² он ошибся?Решение:
10 · 8 = 80 (см²)
8 · 6 = 48 (см²)
80 — 48 = 32 (см²)Ответ: он ошибся на 32 см².
Задача №14
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Решение:
4 + 4 = 8 (см)
36 — 8 = 28 (см)
28 : 2 = 14 (см)
14 · 4 = 56 (см²)Ответ: площадь прямоугольника 56 см².
Задача №15
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см)
3 + 3 = 6 (см)
24 — 6 = 18 (см)
18 : 2 = 9 (см)Ответ: длина прямоугольника 9 см.
Задача №16
Сторона квадрата 18 см.
Найди длину прямоугольника с таким же периметром и шириной 14 см.
Решение:
18 · 4 = 72 (см)
14 + 14 = 28 (см)
72 — 28 = 44 (см)
44 : 2 = 22 (см)Ответ: длина прямоугольника 22 см.
Задача №17
Площадь прямоугольника 40 см². Ширина его 4 см.
Чему равен периметр прямоугольника?Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)Ответ: периметр прямоугольника 28 см.
Задача №18
Площадь прямоугольника 40 см². Длина его 8 см.
Чему равен периметр прямоугольника?Решение:
40 : 8 = 5 (см)
(8 + 5) · 2 = 26 (см)Ответ: периметр прямоугольника 26 см.
Задача №19
Ширина прямоугольника 15 см, длина 20 см.

Найди длину другого прямоугольника с той же площадью, если его ширина в 3 раза меньше ширины первого прямоугольника.Решение:
в первом действии узнаём площадь по формуле a · b = S
15 · 20 = 300 (см²) — S одного и другого прямоугольника
теперь ширину второго
15 : 3 = 5 (см) — ширина другого прямоугольника
и отвечаем на вопрос задачи применив формулу S : a = b
300 : 5 = 60 (см)Ответ: длина другого прямоугольника 60 см.
Задача №20
Длина прямоугольника b = 32 см. Ширина a = 4 см.
Найди длину другого прямоугольника с такой же площадью, если его ширина в 2 раза больше ширины первого прямоугольника.Решение:
узнаем площадь прямоугольников по формуле a · b = S
32 · 4 = 128 (см²) — S первого прямоугольника
теперь ширину второго прямоугольника
4 · 2 = 8 (см) — ширина другого прямоугольника
применив формулу S : a = b узнаем длину другого
128 : 8 = 16 (см)Ответ: длина другого прямоугольника 16 см.
Задача №21
Какой участок земли потребует большую ограду: прямоугольный размерами 32 м и 2 м или квадратный, имеющий ту же площадь?
Решение:
Ⅰ. Прямоугольный участок
32 · 2 = 64 (м²) — S прямоугольного участка = 64 (м²)
(32 + 2) · 2 = 68 (см) — P прямоугольного участка = 68 (см)Ⅱ. Квадратный участок (имеющий площадь прямоугольного = 64 м²)
Если S квадрата = a · a, тогда, из формулы, узнаем сторону квадратного участка S : a = a
(у квадрата все стороны равны, тогда a · a = S — таблицу умножения мы знаем, подберём значения a и заменим их — 8 · 8 = S или 8 · 8 = 64 или 64 = 8 · 8 или 64 : 8 = 8)
64 : 8 = 8 (м) — любая сторона квадратного участка = 8 (м)
8 · 4 = 32 (м) — периметр квадратного участка = 32 (м)Ⅲ. P прям. — P квадр. = разница периметров
68 — 32 = 36 (м) — разница периметровОтвет: потребует большую ограду прямоугольный на 36 м.
Задача №22
Какая комната потребует больше плинтуса: прямоугольная размерами 4 м и 9 м или квадратная, имеющая ту же площадь?
Решение:
(4 + 9) · 2 = 26 (м) — P периметр прямоугольной комнаты
4 · 9 = 36 (м²) — S площадь прямоугольной комнаты
(из условия задачи квадратная комната имеет ту же площадь 36 м², а из определения площади квадрата знаем, что все стороны равны a = a = a = a, смотрим таблицу умножения и видим 6 · 6 = 36, то есть любая из сторон a = 6
запишем (приведём) формулу площади квадрата S = a · a в форму нахождения её стороны S : a = a
36 : 6 = 6 (м) — любая из сторон квадратной комнаты
6 · 4 = 24 (м) — P периметр квадратной комнаты
26 — 24 = 2 (м)Ответ: потребует больше плинтуса прямоугольная на 2 м.
Задача №23
Ребро куба равно 2 сантиметров.
Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)Ответ: площадь всех граней куба равна 24 см².
Задача №24
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Решение:
Для решения потребуются формулы:
S = a · a; S = a² — площадь квадрата (у квадрата все стороны равны)
S = a · b — площадь прямоугольника (у прямоугольника противоположные стороны равны)
Далее всё очень просто:Квадрат A.

S = a · a или a · a = S — формула площади квадрата, тогда
8 · 8 = 64 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
4 · 1 = 4 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь вырезанного прямоугольника
64 — 4 = 60Ответ: площадь получившейся фигуры равна 60.
Квадрат B.
S = a · a или a · a = S — формула площади квадрата, тогда
7 · 7 = 49 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
4 · 2 = 8 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь прямоугольника
49 — 8 = 41Ответ: площадь получившейся фигуры равна 41.
Квадрат C.

S = a · a или a · a = S — формула площади квадрата, тогда
7 · 7 = 49 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
5 · 1 = 5 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь прямоугольника
49 — 5 = 44Ответ: площадь получившейся фигуры равна 44.
Задача №25
- Найдите площадь фигуры, изображённой на рисунке A.
- Найдите площадь фигуры, изображённой на рисунке B.
- Найдите площадь фигуры, изображённой на рисунке C.
- Найдите площадь фигуры, изображённой на рисунке D.
- Найдите площадь фигуры, изображённой на рисунке E.
(!) Фигуры расположены на листе в клетку, где каждая клетка – квадрат со стороной равной 1см.
Определение:
Неправильный четырехугольник – фигура, у которой стороны не равны и не параллельны.
Решение:
разобьём неправильные четырехугольники A, B, D на два прямоугольных треугольника и прямоугольник, а неправильные четырехугольники C, E на два прямоугольных треугольника и квадрат.Применив формулы площади треугольника , квадрата и прямоугольника легко решим поставленную задачу
Фигура A.
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²Ответ: площадь фигуры A 18,5 см²
Фигура B.

S = a · b — формула площади прямоугольника, тогда
5 · 1 = 5 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 6 · 5 = 15 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 1 = 0,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры B
5 + 15 + 0,5 = 18,5 см²Ответ: площадь фигуры B 20,5 см²
Фигура C.
S = a · a; S = a² — формула площади квадрата, тогда
5 · 5 = 25 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 6 = 3 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры C
25 + 3 + 2,5 = 30,5 см²Ответ: площадь фигуры C 30,5 см²
Фигура D.

S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры D
12 + 2,5 + 4 = 18,5 см²Ответ: площадь фигуры A 18,5 см²
Фигура E.
S = a · a; S = a² — формула площади квадрата, тогда
2 · 2 = 4 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 3 · 4 = 6 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 2 = 2 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры E
4 + 6 + 2 = 12 см²Ответ: площадь фигуры E 12 см².
Задача №26
Найдите площади и периметры фигурок. Сделайте вывод.
Определение:
Периметр – сумма длин всех сторон фигуры выраженый в милиметрах, сантиметрах, дециметрах, метрах и т.д.Площадь фигуры – геометрическое понятие, размер плоской фигуры выраженый в мм², см², дм², м² и т.д.
Пусть каждая из сторон клетки равна 1 см, тогда
применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура A имеет четыре стороны, тогда
1 + 4 + 1 + 4 = 10 см — периметр фигуры.Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура B имеет четыре стороны, тогда
2 + 2 + 2 + 2 = 8 см — периметр фигуры.
Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура C имеет шесть сторон, тогда
3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура D имеет восемь сторон, тогда
1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура E имеет восемь сторон, тогда
1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.Вывод:
Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат.
У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача №27
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см
Найдём гипотенузу прямоугольного треугольника по формуле: a² + b² = c²Решение:
6² + 8² = c²
6 · 6 + 8 · 8 = c²
36 + 64 = с²
с² = 36+64
с² = 100
с = 10
Найдём периметр прямоугольного треугольника по формуле: p = a + b + c
p = 6 + 8 + 10 = 24Ответ: периметр прямоугольника равен 24 см.
см. Площадь треугольника
Задача №28
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (гипотенуза) с = 10 см
Найдём гипотенузу прямоугольного треугольника по формуле: a² + b² = c²Решение:
6² + b² = 10²
6 · 6 + b² = 10 · 10
36 + b² = 100
b² = 100 — 36
с² = 64
с = 8
Найдём периметр прямоугольного треугольника по формуле: p = a + b + c
p = 6 + 8 + 10 = 24Ответ: периметр прямоугольника равен 24 см.
см. Площадь треугольника
Задача №29
В треугольной пластине abc у которой один из углов 90°, сторона a равна 20 сантиметрам, а сторона b равна 10 сантиметрам просверлили отверстие диаметром 3 сантиметра. Какую оставшуюся площадь пластины нужно покрасить?
Решение:
Мы знаем что площадь – S треугольника равна половине – ½ произведения его основания – a умноженная на высоту – h, то есть S = ½ · a · h, а Формула площади круга S = πd² : 4, число π ≈ 3,14.
1) По условию задачи пластина имеет форму прямоугольника со сторонами abc, в данном случае сторона b является высотой треугольника.
Тогда формула будет выглядеть так – S = ½ · a · b
подставим значения в эту формулу
½ · 10 · 20 = 100 (см²) — площадь треугольника
2) Подставим значения в формулу и узнаем площадь круга S = πd² : 4
3,14 · 3² : 4 = 3,14 · 9 : 4 = 7,065 (см²)
3) Теперь мы можем ответить на вопрос поставленный в задаче
100 — 7,065 = 92,935 см² — оставшуюся площадь пластиныОтвет: нужно покрасить 92,935 см².
Задача №30
На садовом участке Петя построил для цыплят круглый вольер радиусом 5 метров. Участок имеет прямоугольную форму с длинной 120 метров и шириной равной 8 диаметрам вольера. Сколько потребуется метров металлической сетки чтобы огородить участок и вольер?
Решение:
Для решения задачи нам потребуются вычислить периметры участка и вольера.
1) В первом действии узнаем диаметр вольера, нам известен радиус 5 метров, тогда по формуле диаметр равен двум радиусам D = 2R
5 · 2 = 10 (м) — диаметр вольера
2) Если ширина участка равна 8 диаметрам вольера, тогда
10 · 8 = 80 м — ширина участка
3) Далее по формуле P = (a + b) · 2 — периметр прямоугольника
120 + 80 · 2 = 400 (м)
4) Теперь по формуле P = 2πR — длина окружности (периметр) вольера
2 · 3,14 · 5 = 2 · 3,14 · 5 = 31,4 (м)
5) В последнем действии сложим периметры участка и вольера ответим на вопрос задачи
400 + 31,4 = 431,4 (м)Ответ: потребуется 431,4 метров металлической сетки.
Коротко:
Известные и великие математики
ученые древности, средневековья и современности, и их вклад в мировую науку
Рене Декарт
математик, философ
Дата рождения: 31 марта 1596 г.
Место рождения: Декарт, Турень, Абсолютная монархия во Франции
Дата смерти: 11 февраля 1650 г. (53 года), Стокгольм, Швеция
Биография
Родился 31 марта 1596 года в городе Ла-Э-ан-Турен (ныне Декарт), департамент Эндр и Луара, Франция. Декарт происходил из старинного, но обедневшего дворянского рода, был младшим (третьим) сыном в семье. Начальное образование Декарт получил в иезуитском колле́же Ла Флеш, где его учителем был Жан Франсуа.
В коллеже Декарт познакомился с Мареном Мерсенном (тогда — учеником, позже — священником), будущим координатором научной жизни Франции, и Жаком Валле де Барро. Религиозное образование только укрепило в молодом Декарте скептическое отношение к тогдашним философским авторитетам. Позже он сформулировал свой метод познания: дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.
Позже он сформулировал свой метод познания: дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.
В 1612 году Декарт закончил коллеж, некоторое время изучал право в Пуатье, затем уехал в Париж, где несколько лет чередовал рассеянную жизнь с математическими исследованиями. Затем он поступил на военную службу (1617) — сначала в революционной Голландии (в те годы — союзнице Франции), затем в Германии, где участвовал в недолгой битве за Прагу (Тридцатилетняя война).
В Голландии в 1618 году Декарт познакомился с выдающимся физиком и натурфилософом Исааком Бекманом, оказавшим значительное влияние на его формирование как учёного. Несколько лет Декарт провёл в Париже, предаваясь научной работе, где, помимо прочего, открыл принцип виртуальных скоростей, который в то время никто ещё не был готов оценить по достоинству.
Затем — ещё несколько лет участия в войне (осада Ла-Рошели). По возвращении во Францию оказалось, что свободомыслие Декарта стало известно иезуитам, и те обвинили его в ереси. Поэтому Декарт переезжает в Голландию (1628), где проводит 20 лет в уединённых научных занятиях.
Поэтому Декарт переезжает в Голландию (1628), где проводит 20 лет в уединённых научных занятиях.
В 1634 году он заканчивает свою первую, программную книгу под названием «Мир» (Le Monde), состоящую из двух частей: «Трактат о свете» и «Трактат о человеке». Вскоре, однако, одна за другой, появляются другие книги Декарта.
Кардинал Ришельё благожелательно отнёсся к трудам Декарта и разрешил их издание во Франции. Протестантские же богословы Голландии наложили на них проклятие (1642)
В 1649 году Декарт, измученный многолетней травлей за вольнодумство, поддался уговорам шведской королевы Кристины (с которой много лет активно переписывался) и переехал в Стокгольм. Почти сразу после переезда он серьёзно простудился и вскоре умер.
Его труды:
- Сформулировал (хотя и не доказал) основную теорему алгебры
- Методы решения алгебраических уравнений
- Классификация алгебраических кривых
- Сформулировал точное «правило знаков» для определения числа положительных корней уравнения
- Исследовал алгебраические функции (многочлены)
- Исследования Декарта в области к механики, оптики и общему строению Вселенной
- Математически вывел закон преломления света
- Понятие о рефлексе
- Классическое построение философии рационализма
- Теория близкодействия
- Метод радикального сомнения
- Картезианский дуализм
В память о Декарте:
- Великий физиолог И.
 П. Павлов поставил памятник-бюст Декарту возле своей лаборатории
П. Павлов поставил памятник-бюст Декарту возле своей лаборатории - В честь учёного названы его родной город
- Назван кратер на Луне
- Назван астероид (3587) Descartes
- Декартова система координат
- Декартов лист
- Декартов овал
- Декартово дерево
- Декартово произведение
***
Цитата: У одного человека зачастую больше шансов сделать открытие, нежели у нескольких, занимающихся одной проблемой.
Площадь прямоугольного треугольника через катеты » Kupuk.net
Геометрия — учение о фигурах. Невозможно представить работу архитектора, строителя, модельера, декоратора, инженера и многих других специалистов без знания этой науки. Одной из начальных задач при изучении предмета является обучение нахождения площади прямоугольного треугольника через катеты. Это умение в дальнейшем позволяет успешно решать различные задания на вычисление параметров сложных объектов.
Свойства треугольника
Пожалуй, в жизни любой человек сталкивается с треугольниками. Они бывают разными: остроугольными, тупоугольными, прямоугольными, равнобедренными и равносторонними. Но всех их объединяет один признак — существование трёх углов. Точное определение фигуре дали ещё в Древней Греции. Евклид утверждал, что этот объект состоит из трёх точек, расположенных на разных прямых, и трёх замкнутых линий, поочерёдно соединяющих эти точки.
Они бывают разными: остроугольными, тупоугольными, прямоугольными, равнобедренными и равносторонними. Но всех их объединяет один признак — существование трёх углов. Точное определение фигуре дали ещё в Древней Греции. Евклид утверждал, что этот объект состоит из трёх точек, расположенных на разных прямых, и трёх замкнутых линий, поочерёдно соединяющих эти точки.
Три точки, ограничивающие отрезки, называют вершинами, а линии, соединяющие их, — сторонами. Внутреннюю плоскость, заключённую в линии, называют площадью. Так как отрезки фигуры образуют три угла, то объект относится к классу многоугольников. Замкнутая прямая, соединяющая вершину с серединой противолежащей стороны, носит имя медиана. Всего их может быть три штуки, пересекаться они могут в одной точке, которую называют центроидом. Он является центром тяжести.
Если из угла провести перпендикуляр к противолежащей стороне, то полученная линия будет высотой. Линия, опущенная к стороне напротив угла и разделяющая его пополам, называется биссектрисой.
В любой треугольник можно вписать окружность. Она будет единственной, так как должна касаться всех трёх сторон. Центр круга всегда будет совпадать с местом пересечения биссектрис.
Разделение треугольников происходит по размерам углов и сторон. Например, у равносторонней фигуры любой из трёх углов равен 60 градусам, у равнобедренной — две стороны и два угла равны. Для любого треугольника справедливо утверждать следующее:
- всегда напротив длинной стороны будет находиться больший угол;
- если две стороны равны, то напротив них будут равные углы;
- при сложении значений всех углов сумма составит 180 градусов;
- продолжив сторону за пределы объекта, можно получить внешний угол;
- одна из сторон всегда будет меньше суммы оставшихся и больше их разности.
В элементарной математике часто используют правила, называемые признаками подобия и равенства. Так, при сравнении две фигуры будут равными, если длины их сторон совпадают.
Соответственно, углы тоже станут одинаковыми или будут равными две стороны и угол между ними.
Прямоугольная фигура
Треугольник с одним прямым углом, то есть составляющим 90 градусов, называется прямоугольным. Два отрезка, примыкающие к нему, называют катетами, а прямую, соединяющую их, — гипотенузой. Из любого треугольника можно получить две прямоугольных фигуры. Для этого нужно в нём опустить высоту. Многие свойства многоугольника идентичны прямоугольной фигуре. Два равных треугольника можно объединить в прямоугольник, при этом их гипотенузы будут совпадать с диагональю.
Основную особенность фигуры, которая позволяет посчитать площадь, подметил ещё Пифагор. Она очень простая и записывается как с2 = а2 + b2. В соответствии с этим правилом квадрат гипотенузы равняется результату сложения квадратов катетов, то есть сумма площадей квадратов, достроенных на катетах, совпадает с площадью квадрата, построенного на гипотенузе. Кроме основного свойства, чтобы найти площадь прямоугольного треугольника, нужно знать следующие правила:
Кроме основного свойства, чтобы найти площадь прямоугольного треугольника, нужно знать следующие правила:
- при сложении двух острых углов сумма будет равняться 90 градусов;
- гипотенуза у фигуры всегда будет больше катета;
- длину катета, расположенного напротив угла в 30 градусов, можно найти, разделив гипотенузу пополам;
- катеты в прямоугольном треугольнике одновременно являются его высотами;
- величина радиуса описанной окружности совпадает с медианой.
Из теоремы Пифагора можно сделать важное следствие. Становится очевидным, что высота, опущенная из прямого угла, разделит гипотенузу на два отрезка: c1 = a2/c и c1 = b2/c. Полученные замкнутые линии являются проекциями катетов. В то же время высоту фигуры можно определить, используя следующую формулу: h = √ca + cb.
Если угол, располагающийся напротив катета a, обозначить альфой, а напротив b — бетой, то справедливо утверждать, что гипотенуза будет равняться: c = b /sin b = a / sin a = b / cos a = a / cos b = h = √a2 + b2. Другими словами, длины катетов можно вычислить, используя синус противолежащего угла или косинус прилежащего. То есть получатся равенства: a = c * sin a = c * cos b и b = c * cos a = c * sin b. Учитывая тригонометрические правила, катеты можно найти, используя тангенс. Так, сторона b = a * tg b, катет a = b * tg a.
Другими словами, длины катетов можно вычислить, используя синус противолежащего угла или косинус прилежащего. То есть получатся равенства: a = c * sin a = c * cos b и b = c * cos a = c * sin b. Учитывая тригонометрические правила, катеты можно найти, используя тангенс. Так, сторона b = a * tg b, катет a = b * tg a.
Все рассмотренные формулы и свойства помогают при нахождении площади фигуры. Но кроме них полезно знать и то, что радиус вписанной окружности в прямоугольную фигуру можно узнать, найдя разницу суммы катетов и гипотенузы, разделённую на 2, то есть r = (a + b — c) / 2.
Формулы площади
Найти площадь треугольника с прямым углом можно различными способами. Но проще всего это сделать через катеты. Выражение для нахождения параметра довольно простое: S = (a * b) / 2. Это классическая формула площади прямоугольного треугольника. Существуют и другие формулы:
- S = (a2 * tg b) / 2;
- S = (a2 * ctg a) / 2;
- S = (b2 * tg a) / 2;
- S = (b2 * ctg b) / 2.

Другими словами, площадь можно определить, зная значения двух катетов, длину одного из них и разворот противолежащего или прилежащего угла. Для доказательства теоремы нахождения площади понадобится изобразить фигуры с катетами b и a. Фигуру можно достроить до параллелограмма, отложив параллельные катетам прямые. Вершины полученного объекта можно обозначить буквами A, B, C, D, начиная с прямого угла треугольника и двигаясь влево.
Прямоугольник образуется двумя треугольниками, равными между собой по трём сторонам: AB = CD, AC = BD (ВС — общая сторона). Учитывая равенства, можно утверждать, что площади фигур равны друг другу. Следовательно, площадь параллелограмма можно найти через сумму площадей двух треугольников: S = Sabc + Sacd. Отсюда верным будет утверждение, что площадь начального треугольника ABC равняется половине замкнутой области прямоугольника, а та соответствует произведению сторон: S = a * b, то есть AB * BC.
Эта формула легко доказывается с учётом того, что прямоугольник является фигурой, в которую можно вписать несколько четырёхугольников. Так как общая площадь будет равняться сумме площадей внутренних фигур, то верным будет равенство: (a + b)2 = S + S + a2 + b2 = a2 + 2ab + b2 = 2S + a2 + b2. Отсюда получим, что S = a* b. Следовательно, так как площадь треугольника равняется половине площади прямоугольной фигуры, то можно утверждать, что S = (a * b)/2 = (AB * BC) / 2. Формула доказана.
Так как общая площадь будет равняться сумме площадей внутренних фигур, то верным будет равенство: (a + b)2 = S + S + a2 + b2 = a2 + 2ab + b2 = 2S + a2 + b2. Отсюда получим, что S = a* b. Следовательно, так как площадь треугольника равняется половине площади прямоугольной фигуры, то можно утверждать, что S = (a * b)/2 = (AB * BC) / 2. Формула доказана.
Из этого правила вытекают два следствия:
- площадь равняется половине результата перемножения катетов;
- когда высоты двух треугольных фигур совпадают, их площади можно соотнести как основания.
- если угол одного треугольника равен углу другого, то площади объектов соотносятся как результат умножения сторон с одинаковыми углами.
Использование рассмотренных следствий помогает при решении многих геометрических задач. Они касаются не только треугольников, но и других многоугольных фигур.
Решение задач
Важно не только знать формулы для нахождения площади, но и уметь их применять на практике. Это возможно лишь с опытом, который можно получить, решая различные задания. Существуют определённые задачи, которые ученикам нужно решить самостоятельно. После успешного решения можно утверждать, что учащиеся полностью разобрались в теме, поэтому они могут переходить к следующему разделу геометрии. Вот некоторые задания, позволяющие закрепить теоретический материал:
Это возможно лишь с опытом, который можно получить, решая различные задания. Существуют определённые задачи, которые ученикам нужно решить самостоятельно. После успешного решения можно утверждать, что учащиеся полностью разобрались в теме, поэтому они могут переходить к следующему разделу геометрии. Вот некоторые задания, позволяющие закрепить теоретический материал:
 Из неё можно выразить неизвестный катет. Его длина будет равняться: b = √c2 — a2 = √252 — 152 = √625 — 225 = √400 = 20 см. Известные данные нужно подставить в формулу площади и выполнить расчёт: S = 20 * 15 / 2 = 150 см².
Из неё можно выразить неизвестный катет. Его длина будет равняться: b = √c2 — a2 = √252 — 152 = √625 — 225 = √400 = 20 см. Известные данные нужно подставить в формулу площади и выполнить расчёт: S = 20 * 15 / 2 = 150 см².Длина катета в треугольнике равна 2 * √3 см, а противолежащий ему угол составляет 50 градусов. Необходимо вычислить площадь фигуры. Известно, что сумма углов в таком треугольнике — 180 градусов. Следовательно, разворот прилежащего к катету углу равняется a = 180 — 90 — b = 180 — 90 — 60 = 30 градусов. Теперь можно использовать формулу для нахождения площади прямоугольного многоугольника через катет и тангенс угла: S = (b 2 * tg a) / 2 = ((2 * √3)2 * tg 30) / 2 = (12/2) * (√3/3) = 2√3 см2.
Таким образом, площадь прямоугольной фигуры — ее численная характеристика. Определить ее можно, используя несколько способов. При этом всегда необходимо знать длину хотя бы одного из катетов. Это связанно с тем, что две из трёх высот совпадают с ним.
Найдите площадь и периметр (на случай, если вы их потеряли) (Видео)
Если вам нужна помощь с периметром прямоугольника, перейдите сюда .
TranscriptFAQsPractice
Привет, ребята! Добро пожаловать в это видео о нахождении площади и периметра объекта.
Площадь и периметр помогают нам измерять двумерные фигуры.
Площадь измеряет поверхность объекта, а периметр измеряет длину внешней стороны объекта.
Допустим, у вас есть прямоугольный бассейн.
Вы хотите найти брезент, чтобы накрыть его, тогда вам нужно знать площадь поверхности бассейна (все синее). Но если вы хотите узнать расстояние, которое потребуется вам, чтобы обойти бассейн, вам нужно будет знать периметр.
Теперь давайте посмотрим, как рассчитать каждый из них.
Как найти Периметр
Во-первых, периметр. Чтобы вычислить периметр любого многоугольника, достаточно сложить длины всех сторон.
В качестве примера возьмем наш прямоугольный бассейн. Допустим, что ширина 15 футов, а длина 7 футов.
Поскольку это прямоугольник, мы знаем, что параллельные стороны имеют одинаковую длину.
Итак, у нас есть вся необходимая информация. Теперь просто сложите все стороны.
Начнем с нашей формулы. Допустим, 15 равно \(a\), а 7 равно \(b\).
Итак, мы имеем \(P= a + a + b + b\).
Теперь давайте подставим наши числа. \(P=15\текст{футы}+15\текст{футы}+7\текст{футы}+7\текст{футы}\). Итак, складываем все это и получаем, что наш периметр равен 44 футам.
Мы можем даже упростить формулу периметра прямоугольника. Поскольку мы знаем, что есть 4 стороны и что есть два набора одинаковых сторон (две стороны параллельны друг другу), мы можем упростить нашу формулу до \(P=2(a+b)\). Давайте попробуем и посмотрим, получится ли у нас то же самое.
Давайте попробуем и посмотрим, получится ли у нас то же самое.
\(P=2(15\text{ футов}+7\text{ футов})=2(22\text{ футов})=44\text{ футов}\)
Итак, вы здесь можно увидеть, что мы действительно получаем то же самое.
Мы можем применить тот же принцип для нахождения периметра квадрата. Поскольку у квадрата четыре стороны одинакового размера, мы можем сказать, что периметр квадрата равен \(4\x a\).
Тот же принцип справедлив и для равностороннего треугольника. Все три стороны одинаковы, поэтому мы можем сказать \(P=3\times a\). У равнобедренного треугольника две стороны одинаковы, поэтому мы можем записать нашу формулу периметра как \(P=2a+b\).
Единственная фигура, периметр которой может показаться немного менее очевидным, это наш друг круг. Вы, ребята, возможно, слышали о термине окружности . Окружность — это то же самое, что и периметр круга.
Некоторых математиков может немного смутить термин, который вы используете, потому что технически периметр определяется как «сумма длин ребер замкнутой фигуры», а у круга нет ребер. Но определение окружности — это периметр круга. Итак, как бы вы ни предпочитали называть это, давайте посмотрим, как вы его найдете.
Но определение окружности — это периметр круга. Итак, как бы вы ни предпочитали называть это, давайте посмотрим, как вы его найдете.
Чтобы найти длины окружности , умножьте диаметр на \(π\): (\(C=d\pi\)).
Хорошо, теперь по области.
Как найти площадь
Когда мы смотрели на периметр различных фигур, мы смогли упростить формулы. Давая нам разные формулы для разных форм, но придерживаясь определения сложения всех сторон.
Аналогично, при нахождении площади объекта формула будет разной для разных форм, но каждая формула представляет собой решение для нахождения площади поверхности объекта.
Итак, давайте посмотрим на различные формы и формулу площади, соответствующую каждой форме.
Хорошо, теперь давайте рассмотрим несколько примеров того, как найти площадь эллипса и площадь трапеции.
Допустим, у вас есть эллипс и \(a=6\) и \(b=4\). Теперь давайте подставим наши числа в формулу эллипса.
Допустим, у нас есть трапеция. Мы скажем, что наша высота равна 7, наша сторона \(a\) равна 8, а наша сторона \(b\) равна 5. Теперь мы делаем то же самое, что и в прошлый раз. . Мы просто подставляем наши числа в формулу площади. 92\)
Мы скажем, что наша высота равна 7, наша сторона \(a\) равна 8, а наша сторона \(b\) равна 5. Теперь мы делаем то же самое, что и в прошлый раз. . Мы просто подставляем наши числа в формулу площади. 92\)
Прямоугольник: \(A=lw\)
Треугольник: \(A=\frac{1}{2}bh\)
Параллелограмм: \(A=bh\)
Трапеция: \(A=1/ 2 (b_1+b_2)h\)
Q
Как найти периметр?
A
Найдите периметр, сложив длины каждой стороны фигуры.
пр. Чему равен периметр этой фигуры?
P = 4 + 7 + 3 + 13 + 7 + 20 = 54 в
Q
Как найти площадь треугольника?
А 92\)
Q
Как найти периметр прямоугольника?
A
Найдите периметр прямоугольника, умножив его длину на 2 и ширину на 2 и сложив значения, или добавив его длину и ширину, а затем умножив на 2.
P = 2l + 2w или P = 2(д + ш)
Пр. Чему равен периметр этого прямоугольника?
P = 2(12) + 2(4) = 24 + 8 = 32 дюйма или P = 2(12 + 4) = 2(16) = 32 дюйма
Q
Как найти площадь круг? 92\)
Q
Как найти периметр треугольника?
A
Найдите периметр треугольника, сложив вместе длины всех трех сторон.
Практические вопросы
Вопрос №1:
Какова площадь этого прямоугольника?
52 см 2
133 см 2
47 см 2
154 см 2 9008 Показать2\)
Скрыть ответ
Вопрос №3:
Каков периметр этого прямоугольника?
192 см
176 см
60 см
30 см
Показать ответ
Ответ:
см. Формула периметра прямоугольника:
\(P=2(l+w)\) или
\(P=2l+2w\)
Длина 22см, ширина 8см.
\(P=2(22+8)=2(30)=60\text{ см}\)
Скрыть ответ
Вопрос № 4:
Каков периметр этого пятиугольника?
38 FT
26 FT
42 FT
59 FT
Показать Ответ
Ответ:
Правильный ответ — 38 футов. Найдите периметр на рисунке, добавив длины всех сторон. вместе.
Найдите периметр на рисунке, добавив длины всех сторон. вместе.
\(P=9+9+7+6+7=38\text{ ft}\)
Скрыть ответ
Вопрос №5:
По какой формуле находится периметр прямоугольника?
\(P=4s\)
\(P=2a+b+c\)
\(P=a+b+c\)
\(P=2l+2w\)
Показать ответ
Ответ:
Правильный ответ \(P=2l+2w\). Найдите периметр прямоугольника, прибавив удвоенную длину к удвоенной ширине, или сложите вместе длину и ширину, а затем удвойте это число.
Скрыть ответ
471797
Как найти объем и площадь поверхности для 6 распространенных форм
Как найти объем и площадь поверхности для 6 распространенных форм
Эндрю Ли
23 мая 2021
Онлайн-обучение
,
Геометрия
,
Математика
4 Наш мир наполнен трехмерными объектами.
 Когда дело доходит до знания объема и площади поверхности этих объектов, вам необходимо знать два определения. Площадь поверхности — это площадь всех внешних обращенных поверхностей объекта. Общая площадь поверхности рассчитывается путем сложения всех площадей на поверхности: площадей основания, вершины и боковых поверхностей (боков) объекта. Это делается с использованием различных формул площади и измеряется в квадратных единицах.
Когда дело доходит до знания объема и площади поверхности этих объектов, вам необходимо знать два определения. Площадь поверхности — это площадь всех внешних обращенных поверхностей объекта. Общая площадь поверхности рассчитывается путем сложения всех площадей на поверхности: площадей основания, вершины и боковых поверхностей (боков) объекта. Это делается с использованием различных формул площади и измеряется в квадратных единицах.Объем — это объем пространства, которое занимает трехмерный объект. Существуют также разные формулы для разных трехмерных фигур. Общий объем объекта измеряется в кубических единицах.
Общие формулы для объема и площади поверхности
У нас есть для вас шпаргалка — формулы объема и площади поверхности для обычных форм. Использовать его мудро!
Формулы площади поверхности
Площадь поверхности куба равна 6s² , где s — длина стороны.
Площадь поверхности прямоугольной призмы равна 2(wl + hl + hw) , где w — ширина, h — высота, а l — длина.
Площадь поверхности сферы равна 4πr² , где r — радиус сферы.
Площадь поверхности цилиндра равна 2πrh + 2πr² , где r — радиус цилиндра, а высота — высота.
Площадь поверхности конуса равна πrs + πr² , где r — радиус конуса, а s — наклон.
Формулы объема
Объем куба равен с³ , где s — длина стороны.
Объем прямоугольной призмы равен wlh , где w — ширина, h — высота, а l — длина.
Объем сферы равен ( 4πr³ ) / 3 , где r — радиус сферы.
Объем цилиндра равен πr²h , где r — радиус цилиндра, а высота — высота.
Объем конуса (πr²h) / 3 , где r — радиус конуса, а s — наклон.
Пример расчета объема и площади поверхности
Чтобы найти площадь поверхности объекта с криволинейной поверхностью, например сферы, нет другого выбора, кроме как запомнить формулы объема и площади поверхности. Но для других объектов мы часто можем разбить их на другие узнаваемые многоугольники и формы, объем или площадь поверхности которых мы можем легко найти. Например, в пирамиде вы просто вычисляете площадь основания и добавляете ее к площади поверхности каждой стороны треугольника.
Но для других объектов мы часто можем разбить их на другие узнаваемые многоугольники и формы, объем или площадь поверхности которых мы можем легко найти. Например, в пирамиде вы просто вычисляете площадь основания и добавляете ее к площади поверхности каждой стороны треугольника.
Найдем площадь поверхности и объем квадратной пирамиды с длиной основания 6 дюймов и высотой наклона 5 дюймов.
Площадь поверхности квадратной пирамиды
- Чтобы найти общую площадь поверхности, мы сначала исследуем площадь основания, которое представляет собой просто квадрат. Мы знаем, что площадь квадрата равна b² , где b — длина стороны. В этом случае площадь поверхности составляет 6² или 36 квадратных дюймов.
- Далее мы смотрим на четыре стороны, которые представляют собой просто треугольники. Мы знаем, что площадь треугольника равна (bh) / 2 , где b — основание, а h — высота. В этом случае основание треугольника совпадает с основанием пирамиды, б.
 Высота треугольника равна наклонной высоте пирамиды s. Таким образом, площадь только одной из этих треугольных сторон равна: .
Высота треугольника равна наклонной высоте пирамиды s. Таким образом, площадь только одной из этих треугольных сторон равна: .
- Когда мы складываем четыре из этих треугольников с площадью квадратного основания, мы получаем общую площадь поверхности b² + 4(bs) / 2 или b² + 2bs для квадратной пирамиды. Подставляя числа, мы получаем:
Объем квадратной пирамиды
Объем пирамиды определяется следующей формулой объема:
Мы можем подставить наши значения высоты и основания, чтобы получить:
Распознавание объема и площади27
Опять же, площадь поверхности измеряет площадь всех внешних поверхностей объекта, а объем измеряет внутреннее пространство, занимаемое объектом.
Вы найдете много реальных случаев, когда полезно вычислить площадь поверхности или объем формы, например, количество воды, необходимое для заполнения бассейна (прямоугольная призма), или количество оберточной бумаги, необходимое для оберните свечу (цилиндр) или баскетбольный мяч (шар). Но всегда есть формулы для самых распространенных форм. Хотя полезно пройтись по формулам, прежде чем вам понадобится их использовать, не думайте, что вам нужно запоминать их все! Просто добавьте этот список в закладки, когда он вам понадобится.
Но всегда есть формулы для самых распространенных форм. Хотя полезно пройтись по формулам, прежде чем вам понадобится их использовать, не думайте, что вам нужно запоминать их все! Просто добавьте этот список в закладки, когда он вам понадобится.
Дополнительная помощь с домашним заданием по математике
- Как найти радиус окружности тремя простыми способами
- Три способа найти объем пирамид
- Как определение площади поверхности применяется к 3D-объектам?
Калькулятор площади поверхности
Квадратная пирамида
ч = высота
с = наклонная высота
а = длина стороны
e = длина боковой кромки
г = а/2
В = объем
S to = общая площадь поверхности
S lat = площадь боковой поверхности
S bot = площадь нижней поверхности
Рассчитайте больше с помощью
Pyramid Calculator
Calculator Используйте
Онлайн-калькулятор для расчета площади поверхности геометрических тел, включая капсулу, конус, усеченный конус, куб, цилиндр, полусферу, пирамиду, прямоугольную призму, сферу, сферическую крышку и треугольную призму
Единицы: Обратите внимание, что единицы измерения показаны для удобства, но не влияют на расчеты. Единицы используются для обозначения порядка результатов, таких как футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты дадут V в мм 3 и S в мм 2 .
Единицы используются для обозначения порядка результатов, таких как футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты дадут V в мм 3 и S в мм 2 .
Ниже приведены стандартные формулы для площади поверхности.
Формулы площади поверхности:
Площадь поверхности капсулы
- Объем = πr 2 ((4/3)r + a)
- Площадь поверхности = 2πr(2r + a)
Площадь поверхности круглого конуса
- Объем = (1/3)πr 2 ч
- Площадь боковой поверхности = πrs = πr√(r 2 + ч 2 )
- Площадь базовой поверхности = πr 2
- Общая площадь поверхности
= L + B = πrs + πr 2 = πr(s + r) = πr(r + √(r 2 + h 2 ))Площадь поверхности круглого цилиндра
- Объем = πr 2 ч
- Площадь верхней поверхности = πr 2
- Площадь нижней поверхности = πr 2
- Общая площадь поверхности
= L + T + B = 2πrh + 2(πr 2 ) = 2πr(h+r)Площадь конической усеченной поверхности
- Объем = (1/3)πh (r 1 2 + r 2 2 + (r 1 * r 2 ))
- Площадь боковой поверхности
= π(r 1 + r 2 )s = π(r 1 + r 2 )√((r 1 — r 2 ) 2 + h 2 )- Площадь верхней поверхности = πr 1 2
- Площадь основания = πr 2 2
- Общая площадь поверхности
= π(r 1 2 + r 2 2 + (r 1 * r 2 ) * s)
= π[ r 1 2 + r 2 2 + (r 1 * r 2 ) * √((r 1 — r 2 ) 2 + h 2 ) ]Площадь поверхности куба
- Объем = a 3
- Площадь поверхности = 6a 2
Площадь поверхности полушария
- Объем = (2/3)πr 3
- Площадь криволинейной поверхности = 2πr 2
- Площадь базовой поверхности = πr 2
- Общая площадь поверхности = (2πr 2 ) + (πr 2 ) = 3πr 2
Площадь поверхности пирамиды
- Объем = (1/3)а 2 ч
- Площадь боковой поверхности = a√(a 2 + 4h 2 )
- Площадь базовой поверхности = a 2
- Общая площадь поверхности
= L + B = а 2 + а √ (а 2 + 4h 2 ))
= а(а + √(а 2 + 4h 2 ))Площадь поверхности прямоугольной призмы
- Объем = л/ч
- Площадь поверхности = 2(дв + лв + бб)
Площадь поверхности сферы
- Объем = (4/3)πr 3
- Площадь поверхности = 4πr 2
Площадь поверхности сферической крышки
- Объем = (1/3)πh 2 (3R — h)
- Площадь поверхности = 2πRh
Площадь поверхности треугольной призмы
Площадь верхней поверхности треугольной призмы Формула
\[ A_{top} = \dfrac{1}{4} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]
\[ A_{top} = \dfrac{1}{4} \sqrt{\begin{align}(a+&b+c)(b+c-a)\\&\times(c+a-b)(a+b-c )\конец{выровнено}} \]
Площадь нижней поверхности треугольной призмы Формула
\[ A_{bot} = \dfrac{1}{4} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]
\[ A_{bot} = \dfrac{1}{4} \sqrt{\begin{выровнено}(a+&b+c)(b+c-a)\\&\times(c+a-b)(a+b-c )\конец{выровнено}} \]
Площадь боковой поверхности треугольной призмы Формула
\[ A_{широта} = h (a+b+c) \]Общая площадь поверхности треугольной призмы Формула
\[ A_{tot} = A_{top} + A_{bot} + A_{lat} \]
алгебраическое предварительное исчисление — Рассчитать ширину и высоту прямоугольника, содержащего заданную площадь и соответствующую заданному соотношению.
 {2} =25$ и, следовательно, $x =\sqrt{25}$, то есть $x =5 $. Таким образом, $W = 3 \times 5 =15 $ и $H= 2 \times 5 =10$, и вы можете видеть, что они имеют соотношение $3 : 2$.
{2} =25$ и, следовательно, $x =\sqrt{25}$, то есть $x =5 $. Таким образом, $W = 3 \times 5 =15 $ и $H= 2 \times 5 =10$, и вы можете видеть, что они имеют соотношение $3 : 2$.$\endgroup$
3
$\begingroup$
Искал ответ на тот же вопрос. Просто другие посты для меня слишком сложны. Я вижу это так:
Если вы задали ширину $a$ и высоту $b$ и знаете $\textsf{площадь}$. Вы хотите растянуть каждую сторону с фиксированным соотношением $x$, пока не получите окончательный размер области. Таким образом, вы растягиваете $a$ на $x$, а $b$ на $x$ равняется $\textsf{площади}$. 92&=\frac{\textf{площадь}}{a\cdot b}\\\\
x & = \ sqrt {\ frac {\ textsf {площадь}} {a \ cdot b}}
\end{выравнивание*}$$
$x$ — это отношение, которое вы растягиваете. Таким образом, вы можете умножить $x$ на $a$ и $b$, чтобы получить новый размер $a$ или $b$.
$\endgroup$
$\begingroup$
Допустим:
- $ratio = \frac{x}{y}$
- $площадь = x \cdot y$
Итак:
$x = y \cdot ratio$
9{2}$
$\sqrt{\frac{area}{ratio}} = y$
Теперь, когда у вас есть y:
$x = \frac{area}{y}$
$\endgroup$
$\begingroup$
ПОДСКАЗКА $\rm\displaystyle\ \\frac{W}H = \frac{3}2\ \Rightarrow\ 2\:W = 3\:H\:,\ $ so $\rm\ 300 = 2\:W\:H = 3\:H\:H\ \Стрелка вправо\ H = \ldots $
$\endgroup$
2
$\begingroup$
Для тех, кто ищет ответ в виде формулы, которую можно «вставить» в Microsoft Excel (или аналогичные приложения), вот что сработало для меня:
Допустим, у вас есть три именованные ячейки в Excel:
-
oldX: ширина текущего изображения -
oldY: высота текущего изображения -
нужная область: нужная область (x*y) изображения после изменения размера.
- Например, если вы хотите, чтобы 9005 Окончательная область — MASTED % из
ТОПРИЯТЕЛЬНА (AreaCaleEG.,0,5для 50 %), 9087 EG.,0,57 для 50 %), 9088 EG.,0,5для 50 %), .желаемая площадь=( старое X * старое Y * масштаб области ).
- Например, если вы хотите, чтобы 9005 Окончательная область — MASTED % из
…наконец-то можно рассчитать новые значения для Y , then for X :
Formula for newY is =FLOOR( SQRT( desiredArea / (oldX/oldY), 1)
Formula for newX is =FLOOR ( (oldX * oldY) / newY, 1 )
(Это была моя интерпретация ответа Лукаса Y выше.)
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Как найти площадь прямоугольника?
11 августа 2022 г.
Как найти площадь прямоугольника?
Содержание
Как найти площадь прямоугольника? Найти площадь прямоугольника несложно. Чтобы найти площадь прямоугольника, умножьте длину на ширину. Это простой расчет для любого прямоугольника, большого или маленького.
Например, если у вас есть прямоугольник длиной 10 футов и шириной 5 футов, вы должны умножить 10 на 5, чтобы получить площадь 50 квадратных футов. Если у вас есть меньший прямоугольник с размерами 2 фута в длину и 1 фут в ширину, вы должны умножить 2 на 1, чтобы получить площадь в 2 квадратных фута.
Знание того, как вычислить площадь прямоугольника, полезно по многим причинам. Во-первых, это может помочь вам измерить размер комнаты или другого пространства. Это также может быть полезно при расчете того, сколько материала вам понадобится для покрытия определенной площади поверхности.
Площадь прямоугольника — это количество квадратных единиц, которое требуется, чтобы покрыть прямоугольник.
Чтобы найти площадь прямоугольника, нужно знать длину и ширину прямоугольника. Формула вычисления площади прямоугольника: A=LxW.
Формула площади прямоугольникаПлощадь прямоугольника вычисляется путем умножения длины на ширину. Если у прямоугольника диагонали пересекаются посередине, то площадь рассчитывается по теореме Пифагора.
A = lw
A = bh
где «A» — площадь, «l» — длина, «w» — ширина, а «b» и «h» — основание и высота треугольника, соответственно.
Этапы вычисления площади прямоугольника Есть несколько шагов, которые вы можете выполнить, чтобы вычислить площадь прямоугольника. Первым делом необходимо измерить длину и ширину прямоугольника. Когда у вас есть эти измерения, вы можете вычислить площадь прямоугольника. Формула вычисления площади прямоугольника: A = lw.
Формула вычисления площади прямоугольника: A = lw.
Итак, когда у вас есть длина и ширина прямоугольника, вы можете подставить эти числа в уравнение, чтобы найти площадь. Еще одна вещь, о которой следует помнить, это то, что площадь квадрата равна 1 квадратной единице, поэтому, если вам нужно найти площадь квадрата, просто используйте длину и ширину квадрата вместо прямоугольника.
Вот четыре простых шага, которые помогут вам вычислить площадь прямоугольника:
1. Измерьте длину и ширину прямоугольника.
2. Умножьте длину на ширину, чтобы получить площадь.
3. При необходимости округлите ответ в большую или меньшую сторону до ближайшего целого числа.
4. Готово! Вы вычислили площадь прямоугольника!
Вычисление площади прямоугольника — это простой процесс, который можно выполнить с помощью элементарной алгебры. Сначала длина и ширина прямоугольника возводятся в квадрат, а затем суммируются. Затем эту сумму делят на 2, чтобы найти площадь прямоугольника. Вывод можно показать на следующем примере: 92 = 25 + 16 = 41 41/2 = 20,5 Следовательно, площадь прямоугольника равна 20,5 квадратных футов.
Затем эту сумму делят на 2, чтобы найти площадь прямоугольника. Вывод можно показать на следующем примере: 92 = 25 + 16 = 41 41/2 = 20,5 Следовательно, площадь прямоугольника равна 20,5 квадратных футов.
Вам когда-нибудь было интересно, почему площадь прямоугольника равна произведению длины на ширину? Прямоугольники — одни из самых простых фигур в геометрии, и их площади можно вычислить довольно легко. На самом деле площадь прямоугольника равна произведению его длины на ширину. Но почему это?
Простой ответ заключается в том, что форма прямоугольника поддается такому расчету. Длина и ширина перпендикулярны друг другу, поэтому в местах пересечения они образуют прямые углы. Это означает, что вся площадь поверхности прямоугольника может быть рассчитана с использованием этих двух измерений.
Не все фигуры можно описать с помощью двух измерений, но прямоугольники являются исключением. Вот почему площадь прямоугольника всегда равна длине x ширине — это просто самый эффективный способ ее вычисления!
Часто задаваемые вопросы В: Каков периметр прямоугольника?
A: Периметр — это расстояние вокруг внешней стороны прямоугольника. Вы можете найти периметр, умножив длину прямоугольника на 2, а затем прибавив ширину прямоугольника.
Вы можете найти периметр, умножив длину прямоугольника на 2, а затем прибавив ширину прямоугольника.
В: Что такое единица площади?
A: Единицей площади является квадратный метр. Это единица, которая используется для измерения объема пространства, занимаемого объектом. Его можно использовать для измерения размера комнаты, участка земли или чего-то еще, что имеет определенную площадь.
В: Площадь прямоугольника равна площади квадрата?
A: Когда дело доходит до площади прямоугольников и квадратов, многие считают, что они одинаковы. Тем не менее, это не всегда так. Площадь прямоугольника определяется как длина, умноженная на ширину, а площадь квадрата определяется как длина, умноженная на длину.
Это означает, что прямоугольник может быть шире или уже квадрата, что изменит его площадь. Однако в большинстве случаев площади прямоугольников и квадратов очень близки друг к другу.
Как решить проблемы с геометрией с участием прямоугольников и треугольников
Ключевые члены
O Точка
O Линия
O СЕГМИГ. о Зона
о Зона
o Square
o Треугольник
Цели
o Познакомьтесь с некоторыми фундаментальными геометрическими рисунками
o Рассчитайте периметр и область прямоугольника
o
Геометрия изучает точки, линии, фигуры, углы и отношения между ними. Мы рассмотрим некоторые простые формы, такие как треугольники и прямоугольники, и обсудим, как вычислить некоторые их свойства.
Элементы геометрии
Прежде чем рассматривать некоторые более сложные фигуры, мы должны иметь представление об определенных терминах, которые используются при изучении геометрии. Несколько основных геометрических понятий включают точки, линии и углы. Точка — это, по сути, местоположение — оно часто изображается с помощью маленькой точки и представляет собой местоположение в пространстве и не имеет ни длины, ни ширины, ни глубины. Несколько точек показаны ниже.
Линия в геометрии имеет почти те же характеристики, что и в реальной жизни (и в алгебре). Геометрическая линия прямая и бесконечно простирается в противоположных направлениях. Если две прямые пересекаются в одной точке, то говорят, что они пересекаются на раз. Пример строки показан ниже; обратите внимание, что на концах линии есть стрелки, указывающие на то, что линия продолжается бесконечно.
Конечная часть линии называется сегмент линии. Отрезки линий имеют длины, которые являются конечными (ограниченными) числами, в отличие от линий, длина которых бесконечна (неограничена). Отрезок линии показан ниже; концы отрезка показаны точками.
Луч — это часть линии только с одной конечной точкой, как показано ниже. Его длина по-прежнему бесконечна, но у него есть один опознаваемый конец.
Когда две прямые, отрезки, лучи или их комбинации пересекаются, они образуют 9угол 0005. Пример угла показан ниже.
Пример угла показан ниже.
Углы можно измерять в градусах (°) в диапазоне от 0° до 360°. Некоторые примеры угловых измерений показаны ниже.
Используя эти основные геометрические термины и фигуры, мы можем теперь перейти к изучению некоторых более сложных фигур.
Прямоугольники
Прямоугольник представляет собой особый вид замкнутой геометрической фигуры с четырьмя сторонами; пример прямоугольника показан ниже.
Прямоугольники можно описать двумя их измерениями: длиной (которую мы можем назвать l ) и шириной (которую мы можем назвать w ). Противоположные стороны прямоугольника равны по длине, а все «внутренние» углы равны 90°; таким образом, мы можем нарисовать прямоугольник, как показано ниже.
Одной из характеристик прямоугольника, которую мы можем легко вычислить, является его периметр, который представляет собой сумму длин всех сторон. Периметр P — следующее:
Периметр P — следующее:
P = L + W + L + W
Мы можем упростить это выражение, преобразуя добавление подобных терминов в умножение:
P =
P =
P = l + l + w + w
P = 2 l + 2 w
Например, рассмотрим прямоугольник ниже.
Поскольку противоположные стороны равны по длине, две стороны прямоугольника имеют длину 6 единиц и две стороны длины 3 единицы. Таким образом, периметр будет следующим:
Хотите узнать больше? Почему бы не пройти онлайн-курс Pre-Algebra?
Периметр 18 единиц. (Обратите внимание, что «единицами» могут быть дюймы, футы, метры или любой другой тип измерения длины. Если единица измерения указана, используйте эту конкретную единицу; в противном случае достаточно общего термина «единицы». )
)
Практическая задача : Вычислите периметр прямоугольника ниже. Все измерения указаны в футах.
Решение : Напомним, что противоположные стороны прямоугольника равны по длине. Таким образом, этот прямоугольник имеет две стороны длиной 10 футов и две стороны длиной 2 фута. Тогда периметр P будет следующим:
В качестве альтернативы мы могли бы просто использовать формулу, полученную выше.
Практическая задача : Некоторый прямоугольник имеет периметр 50 метров и длину 14 метров. Какова его ширина?
Решение : Мы можем решить эту задачу, внимательно изучив представленную информацию и применяя то, что мы знаем о решении уравнений. Мы знаем, прежде всего, что периметр P прямоугольника подчиняется следующей формуле, где l — длина, а w — это ширина.
Постановка задачи говорит нам, каков периметр ( P ), а также какова длина ( l ). Давайте введем эти значения в приведенное выше уравнение, а затем максимально упростим результат.
Чтобы найти ширину прямоугольника, нам нужно найти только w , используя тот же подход, который мы использовали при решении линейных уравнений.
Thus, the width of the rectangle is 11 meters. Давайте проверим этот результат, чтобы убедиться, что он работает. Из условия задачи мы знаем, что длина прямоугольника равна 14 метрам.
Таким образом, ответ подтверждается.
Мы также можем вычислить площадь прямоугольника, которая является мерой того, сколько места он занимает. Рассмотрим прямоугольник шириной 4 единицы и длиной 2 единицы.
Рассмотрим прямоугольник шириной 4 единицы и длиной 2 единицы.
Разделим каждую сторону на сегменты длиной 1, как показано ниже.
Теперь, используя эти деления, мы нарисуем сетку, которая разделит прямоугольник.
Обратите внимание, что сетка разделена на более мелкие области, каждая сторона которых имеет длину 1 единицу.
Каждая из этих меньших областей представляет собой квадрат (прямоугольник, длина и ширина которого равны) со сторонами длины 1. Определим одну из этих областей как 1 квадратную единицу — квадрат, размеры которого (длина и ширина) равны 1 единице. Теперь обратите внимание, что прямоугольник имеет в общей сложности 8 квадратных единиц, которые разделены на два ряда по четыре или четыре ряда по два (в зависимости от того, как вы смотрите на диаграмму). Но вычислить количество объектов (в данном случае квадратных единиц) в строках и столбцах можно путем умножения: обратите внимание, что количество квадратных единиц в прямоугольнике — это просто произведение длины и ширины. Таким образом, площадь A прямоугольника длиной l и шириной w является произведением l и w:
Но вычислить количество объектов (в данном случае квадратных единиц) в строках и столбцах можно путем умножения: обратите внимание, что количество квадратных единиц в прямоугольнике — это просто произведение длины и ширины. Таким образом, площадь A прямоугольника длиной l и шириной w является произведением l и w:
Эта формула применима к любому прямоугольнику, независимо от длины его сторон. (То есть длины могут быть целыми положительными, дробными, десятичными, рациональными или иррациональными числами.)
Например, предположим, что у нас есть прямоугольник длиной 5 дюймов и шириной 3 дюйма, как показано ниже.
Наша цель состоит в том, чтобы вычислить, сколько квадратов со стороной в 1 дюйм может поместиться в этот прямоугольник. Результатом будет общая площадь прямоугольника. Располагая квадраты краем к краю, мы можем разместить пять из них поперек прямоугольника и три по прямоугольнику.
Из диаграммы видно, что в прямоугольник можно поместить 15 квадратов размером в один квадратный дюйм, т. е. прямоугольник имеет площадь 15 квадратных дюймов. Конечно, на это указывает и формула:
Практическая задача : Вычислить площадь прямоугольника шириной 32 дюйма и длиной 3,2 дюйма.
Решение : Формула площади прямоугольника применяется независимо от используемых чисел (конечно, если они положительные). Таким образом, давайте просто воспользуемся формулой для площади A:
Треугольники
Мы также можем рассмотреть некоторые характеристики другой распространенной геометрической фигуры: треугольника. Треугольник — замкнутая геометрическая фигура с тремя сторонами; примеры треугольников показаны ниже.
Периметр треугольника вычисляется почти так же, как периметр прямоугольника: просто сложите длины сторон треугольника (в этом случае у фигуры только три стороны, и эти стороны могут быть разной длины). Однако рассчитать площадь несколько сложнее. Для прямоугольников мы смогли увидеть площадь просто как ряды и столбцы квадратов. Из-за формы треугольника мы не можем аккуратно вписать в него квадраты.
К нахождению площади треугольника мы должны применить несколько иной подход. Давайте рассмотрим общий треугольник, показанный ниже; этот треугольник не имеет особых свойств.
Теперь определим два характерных размера этого (или любого) треугольника: длину основания (обозначим b ) и высоту (обозначим h ). Основание — это просто длина стороны «на земле» или внизу фигуры. Тогда высота является максимальным расстоянием, на которое треугольник достигает «над землей».
Площадь треугольника равна A. Если бы у нас было два таких треугольника совершенно одинаковой формы, общая площадь двух треугольников тогда была бы 2 A. Давайте воспользуемся этим фактом. попытаться построить более знакомую фигуру.
Сначала разрежем один из треугольников по высоте.
Обратите внимание, что оба разделенных треугольника имеют высоту h (точно так же, как мы определили для исходного треугольника) и что их основания равны x и y, , где x + y равно b. Мы не знаем, что такое х и х , но поскольку мы разрезали треугольник, мы знаем, что эти два основания должны в сумме давать основание исходного треугольника. Теперь давайте попробуем переставить части так, чтобы получился прямоугольник!
Давайте теперь рассмотрим характеристики этой новой фигуры (помните, ее площадь 2 A, , где A — площадь исходного треугольника).
Фигура представляет собой прямоугольник — обратите внимание, что противоположные стороны равны по длине (помните, что x + y = b ). Но мы знаем, как вычислить площадь прямоугольника: это просто произведение длины и ширины (в данном случае b и h ). Однако эта общая площадь равна , удвоенной по площади исходного треугольника. Таким образом, произведение b и h равно 2 A.
Изучая линейные уравнения, мы узнали, как решать линейные уравнения для конкретной переменной. В этом случае мы можем выделить A , умножив обе части выражения на .
Таким образом, мы получили формулу площади треугольника. Этот вывод, хотя и не показан в полной математической строгости, дает правильную формулу площади для всех треугольников, а не только для показанного выше.




 А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так: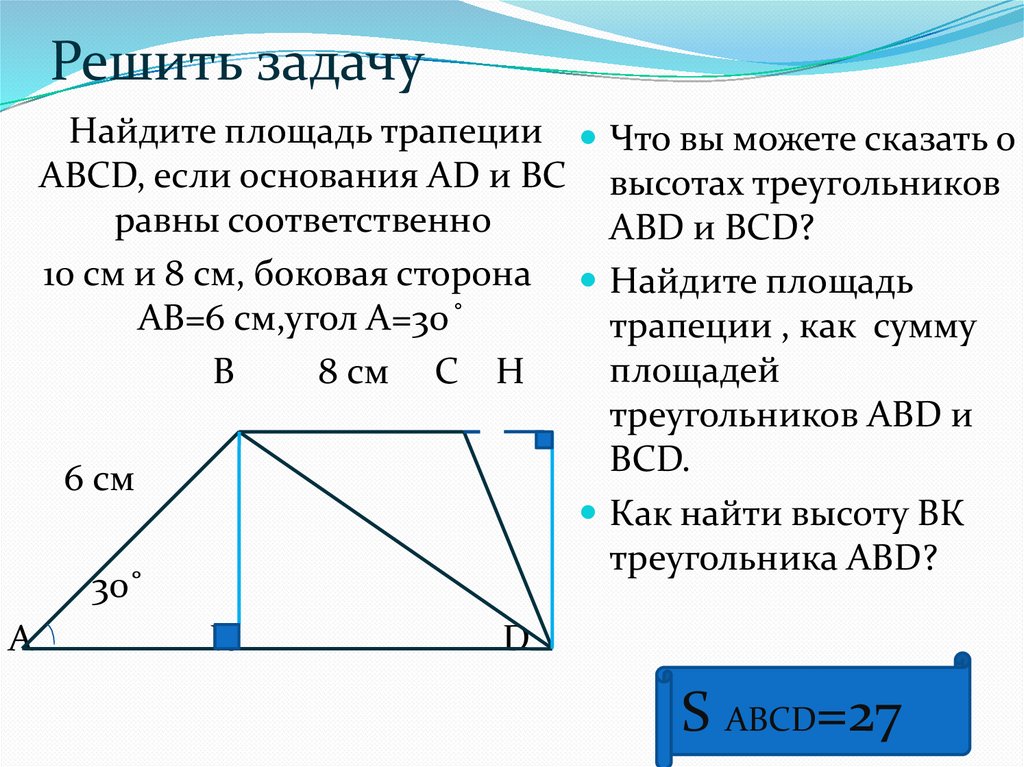
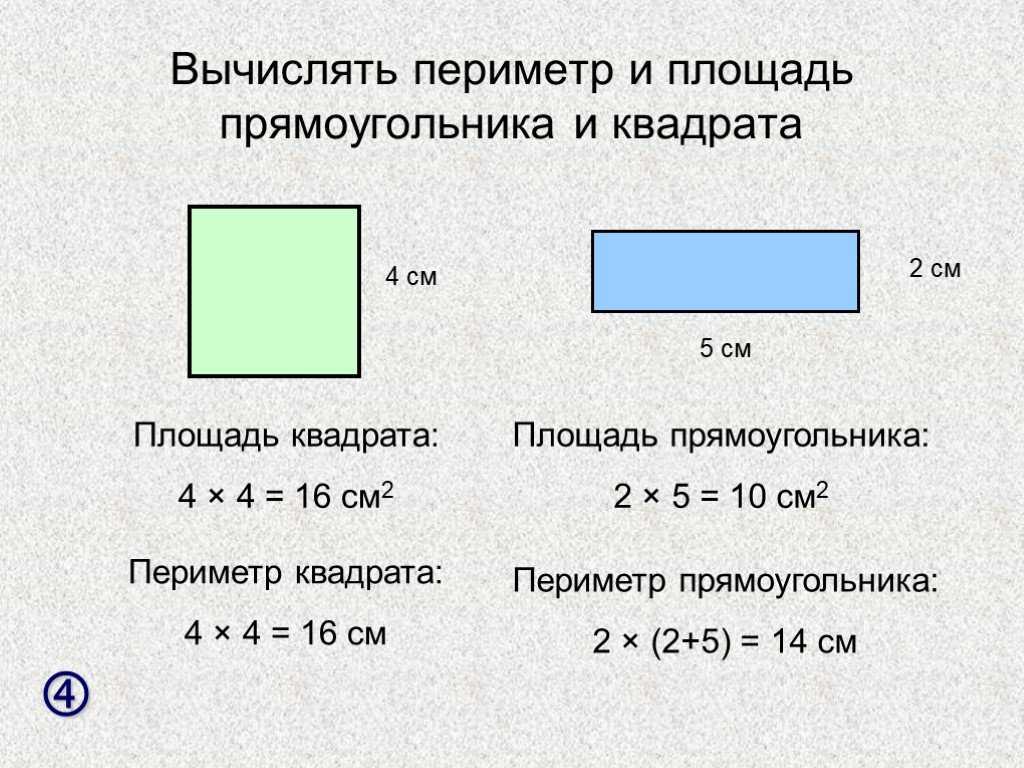 Планиметрия. Равнобедренный треугольник (вариант 1)
Планиметрия. Равнобедренный треугольник (вариант 1)

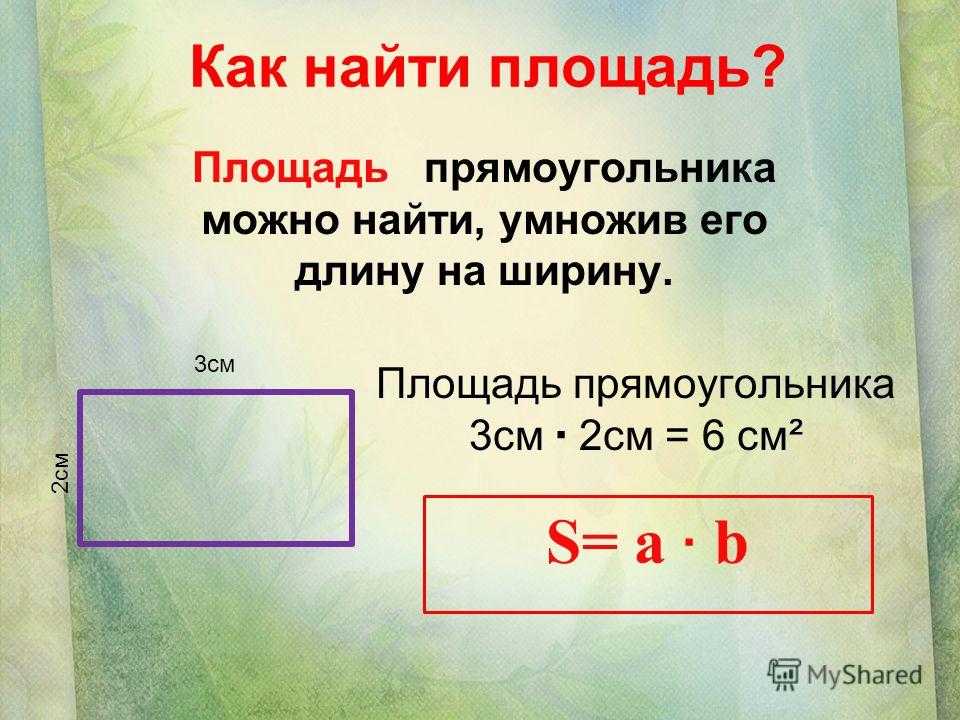

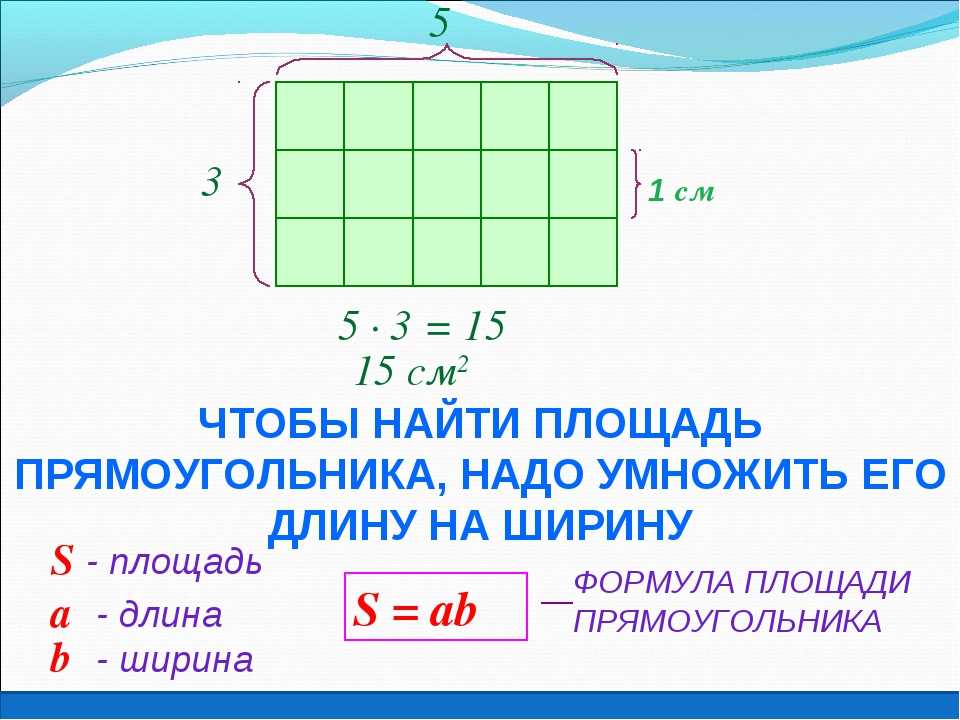

 Найди длину прямоугольника с таким же периметром и шириной 14 см.
Найди длину прямоугольника с таким же периметром и шириной 14 см.


 Найти площадь всех граней куба.
Найти площадь всех граней куба.