Как вычислить градус угла: Калькулятор расчета углов треугольника зная длину сторон

Как высчитать градусы угла

Содержание

• 1 Нахождение углов треугольника по заданным сторонам
• 2 Как вычислять углы
• 3 Как высчитать угол прямоугольного треугольника в градусах?
• 4 Математика
  • 4.1 Строка навигации
• 5 Измерение углов и дуг круга
• 6 Как измерить угол между стен. Несколько способов.
  • 6.1 Какой угол образуют стены. Первый способ – измерение.
  • 6.2 Какой угол образуют стены. Второй способ – расчёт.

Нахождение углов треугольника по заданным сторонам

Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.

От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.

Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).

Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c” class=”pc-math” />
a” class=”pc-math” />
b” class=”pc-math” />

В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.

Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)

Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.

Как вычислять углы

В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.

Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.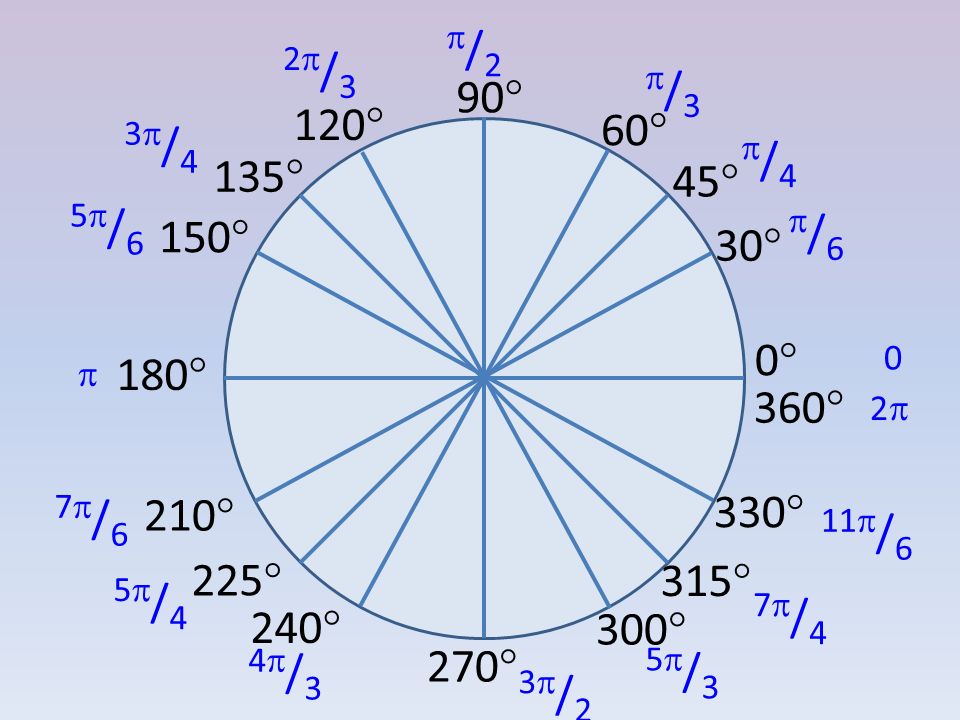

Количество просмотров этой статьи: 127 859.

В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.

Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны, в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.

Как высчитать угол прямоугольного треугольника в градусах?

Если известны размеры трёх сторон, как высчитать угол в градусах?

Да, треугольник на рисунке не так, чтобы уж очень прямоугольный. 2 )/ (2*600*800)=-0,20937

По табличке Брадиса или в своём супер-пупер телефоне находим: 91,2 градуса

Для вычисления углов необходимо обратиться к тригонометрии.

Нам необходимо вычислить величину острого угла А. Для этого используем формулу синуса: ВС/АС (800:1010) = 0,79207920792079.

Зная синус угла А, смотрим в таблицу Брадиса и определяем, что наш угол А равен примерно 52 градусам.

Так как сумма углов треугольника равна 180 градуса, и нам известна величина углов В и А, то мы легко можем узнать величину угла С= 180 – 90-52=38.

Ответ: угол А 52 градуса, угол С 38 градусов.

Математика

Строка навигации

Измерение углов и дуг круга

186. В самом начале курса геометрии было установлено, что значит равные углы, что значит один угол больше другого и что значит найти сумму двух углов, причем, чтобы не делать каких-либо ограничений, надо принять во внимание п. 19, где угол рассматривается, как результат поворота луча около точки (в плоскости). Благодаря этому, углы составляют систему величин, а каждый отдельный угол является определенным ее значением.

Так как здесь налицо те же основные положения, как и при рассмотрении отрезков, то все, что мы нашли для отрезков, справедливо и для углов: также можно измерять углы, принимая один из них за единицу, или находить отношение двух углов.

Чтобы измерять отрезки, нужно было только одно умение (пп. 165 и 172): откладывать на большем отрезке меньший. Так же точно, чтобы выполнять измерение углов, мы должны уметь откладывать меньший угол на большем, – а это мы умеем делать, умеем отличать больший угол от меньшего и умеем строить угол, равный данному.

Что же касается приближенного измерения углов (подобного изложенному в п. 181 для отрезков), то мы можем средствами геометрии лишь выполнять эти измерения с точностью до ½, ¼, 1/8, 1/16 и т. д., так как умеем угол делить только на 2, 4, 8, 16 и т. д. Равных частей. Существуют механические способы деления угла на сколько угодно равных частей.

За единицу при измерении углов принимают прямой угол, в предыдущем курсе мы часто встречались с углами, измеренными прямым углом. Например, если в равнобедренном треугольнике один угол прямой, то каждый из остальных = ½ прямого (½ d), каждый из углов равностороннего треугольника = 2/3 d, сумма внутренних углов n-угольника = 2d (n – 2) и т. д.

Но эта единица оказывается очень велика и на практике берут другую единицу, которая = 1/90 части прямого угла (1/90 d) и которая называется угловым градусом, при письме обозначают эту единицу знаком (°) и, следовательно,

угол равностороннего треугольника = 2/3 d = 60°,
сумма углов треугольника = 2d = 180° и т. д.

Затем вводят еще единицы: угловой градус делят на 60 равных частей, и такую часть называют угловою минутою, – ее знак (‘), угловую минуту делят еще на 60 равных частей и такую часть называют угловой секундою, – ее знак (”).

Например, имеем ¼ d = 22°30′, 1/16 d = 5°37’30”.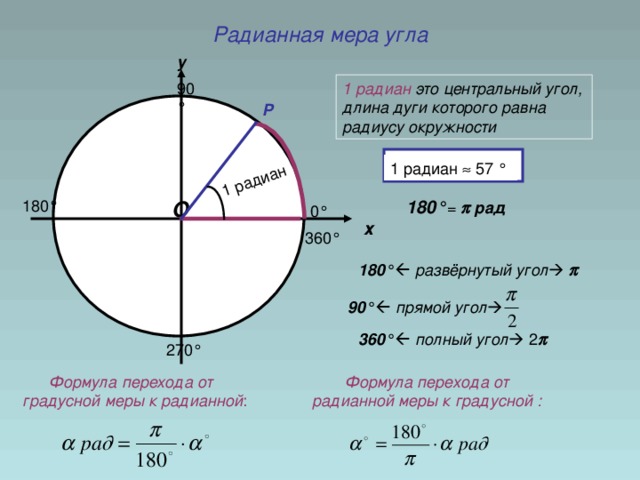

Деление прямого угла на 90 равных частей, а углового градуса на 60 равных частей и т. д. Нельзя выполнять геометрически (циркулем и линейкою), а возможно лишь выполнять механическими способами.

187. Упражнения. 1. Часы показывают 25 минут второго. Вычислить в градусах угол между стрелками часов.

2. Вычислить в градусах (минутах и секундах) внутренний угол правильного 8-угольника, 12-угольника, 20-угольника (его еще мы не умеем строить), 14-угольника (его геометрическими способами невозможно построить).

3. Даны 2 угла, найти отношение этих углов, полагая, что при отыскании общей меры этих углов дойдем до остатка, о котором можно, хоть приближенно, принять, что он укладывается в предыдущем целое число раз (наложение одного угла на другой надо выполнять при помощи циркуля).

188. В п. 21 мы научились различать равные дуги одного круга (или равных кругов) и неравные дуги (знаем, что значит одна дуга больше другой), составили понятие о сумме двух дуг.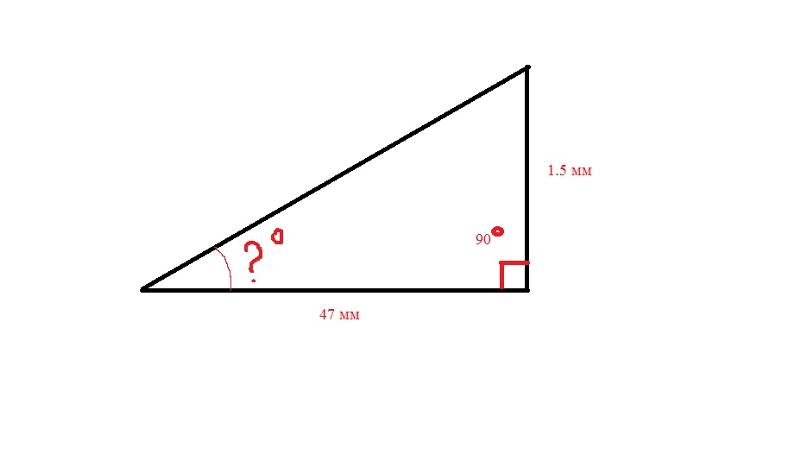 Надо лишь иметь в виду, что сумма нескольких дуг может оказаться больше всего круга: прикладывая к одной дуге другую, к полученной сумме третью и т. д., можем обойти весь круг и зайти за ту точку, где начинается первая дуга. На основании этих сведений мы также, как и для отрезков, можем утверждать, что дуги одного круга можно выражать числами, принимая за единицу любую дугу. Для выполнения измерения дуг необходимо лишь одно умение, – умение откладывать равные дуги, а это можно выполнять при помощи циркуля, которым можно откладывать равные хорды: равным хордам соответствуют равные дуги (п. 119).

Обычно за единицу при измерении дуг принимают 1/360 часть всей окружности, разделить окружность на 360 частей геометрическими способами мы не можем, можем достигнуть этого механическими приемами (п. 148). Эта единица называется дуговым градусом , дуговой градус делят еще на 60 равных частей и эту часть называют дуговою минутою , разделив последнюю на 60 равных частей, получим дуговую секунду .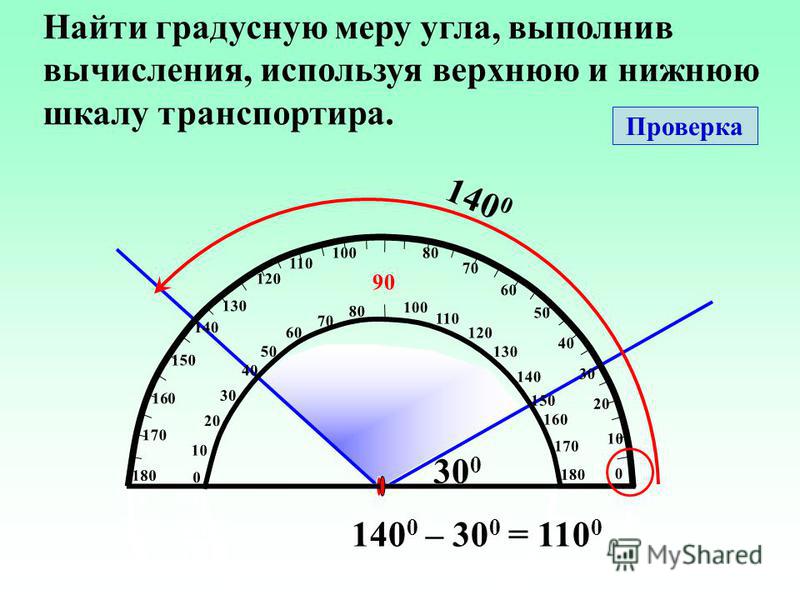 Знаки для их обозначения употребляются такие же (°, ‘ и ”) как и для угловых градуса, минуты и секунды. Недоразумения здесь быть не может, так как всегда видно, об измерении угла или дуги идет речь. Например,

∠AOB = 56° 8′ 24” и ◡MN = 17° 42′ 5”

(в первом случае угловые единицы, во втором — дуговые).

189. В том случае, когда две дуги одного круга или два угла несоизмеримы, отношение этих дуг или отношение этих углов признается нами равным какому-то иррациональному числу. Однако, мы не можем утверждать, что эти числа таковы же, как и те, которым равны отношения каких-либо двух отрезков: чтобы это утверждать, надо было бы убедиться, что для любой пары углов (или дуг одного круга) можно было бы построить два таких отрезка, чтобы можно было признать отношение двух углов (или дуг круга) равным отношению двух построенных отрезков, т. е. чтобы быть убежденным, что всякое рациональное число, большее одного из этих отношений, больше и другого, и всякое рациональное число, меньшее одного из этих отношений, меньше и другого.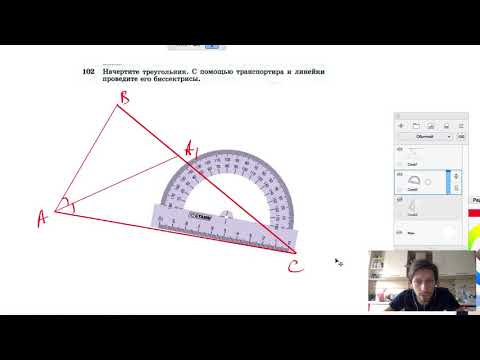 Геометрического решения указанного вопроса (построить требуемые два отрезка) вообще не возможно, но общая теория иррациональных чисел позволяет утверждать, что отношение двух несоизмеримых значений одной и той же системы величин (напр., углов) дает иррациональное число, которое можно рассматривать, как отношение двух несоизмеримых отрезков.

190. В частном случае мы можем легко усмотреть, что отношение двух углов равно отношению двух определенных дуг.

Построим круг O (чер. 194) и два центральных угла ∠AOB и ∠COD, которые опираются соответственно на дуги AB и CD. Рассмотрим два отношения ∠AOB/∠COD и ◡AB/◡CD. Найдем самое большое число со знаменателем n, чтобы оно было меньше первого отношения. Для этого разделим ∠COD на n равных частей (выполнить на самом деле такое построение мы можем лишь тогда, когда число n есть степень числа 2, т. е. 4, 8, 16, 32 …, если же число n какое-либо иное число, то все дальнейшее должно основываться на допущении, что существует угол, хотя мы его построить и не умеем, составляющий 1/n часть данного ∠COD) и станем такие углы укладывать на угле AOB, – допустим, что их уложится m с остатком KOB (∠KOB

Как измерить угол между стен.

Несколько способов.

Какой угол образуют стены. Первый способ – измерение.

Для проектирования мебели мы не только должны измерять длину и высоту стен в квартире или доме, но и необходимо измерить угол в который будет установлена мебель.

Для чего это нужно делать? – чтобы не возникали проблемы с монтажем, чтобы избежать огромные боковые щели, и для того чтобы еще на производстве можно было проводить необходимые корректировки.

К примеру развернутый угол не позволит смонтировать угловую кухню без дополнительных подрезов внутренних угловых модулей и столешницы. Острый угол может потянуть выход корпуса мебели за габариты установочных размеров, потому что в влотную в угол невозможно установить мебельный модуль.

Собственно, когда причины выяснили и необходимость измерения угла очевидна – дело за малым – измерить угол.
Если у Вас имеется в домашнем арсенале угломер – тогда без проблем, а если нет, то нижеописанный способ всегда прийдет на помощь.

Первое что необходимо сделать – это отметить две точки на стенах в одном уровне (на высоте где будет установлен мебельный модуль) следующим образом:

• От угла рулеткой отмеряете по левой и правой стене размер к примеру 500мм. и ставите точки.
• Далее измеряете диагональ – т.е. расстояние между точками.

Итак например у нас есть три размера – катет 500мм., 500мм. и диагональ 700мм.

Следующий этап -это построение угла на шаблоне из любого материала. В нашем случае я покажу как это сделать в программе autоcad, но тоже можно сделать имея циркуль, линейку, транспортир и материал для шаблона.

1. Чертим горизонтально отрезок 500мм. с точками “АБ”. (см. чертеж ниже.)
2. Чертим окружность с радиусом 500мм. с центром в точке “В”.
3. Чертим вторую окружность с радиусом 700мм. с центром в точке “А”.
4. В точке пересечения окружностей ставим точку “С”.
5. Соединяем точки “В” и “С” отрезком и получаем наш угол.
6. Далее остается измерить угол транспортиром на шаблоне или специальным инструментом в программе autоcad. и уже имеющийся чертеж применить для проектирования.

Когда чертеж построен, мы можем в заключении сделать вывод – измеряемый угол 89градусов, угол острый и негативно повлиять на установку мебели он не сможет, т.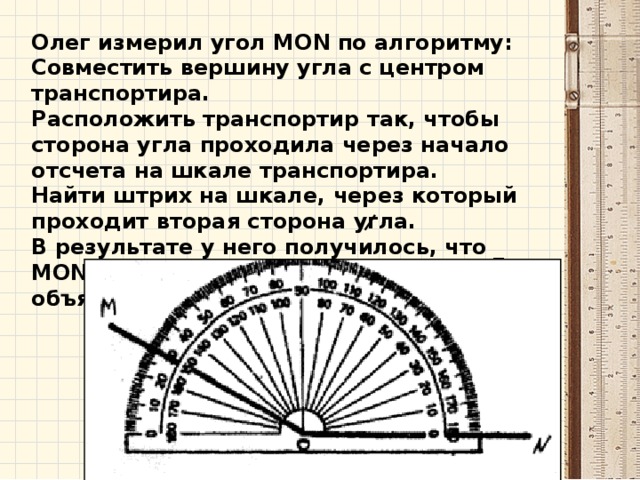 к. 1 градус величина довольно малая.

Какой угол образуют стены. Второй способ – расчёт.

1. От угла отмеряем 1000 мм (чем больше, тем лучше – погрешность меньше… конечно если вы для полочки 400*400 мм, то больше чем 400 мм отмерять не надо) на обеих стенах, и ставим отметки (если обои то можно иголками),
2. Замеряем расстояние между отметками (лучше делать это вдвоем, опять же из соображений точности), допустим у нас получилось 1500 мм.

Осталось рассчитать, сколько градусов в вашем угле по формуле: cos(γ) = (a 2 + b 2 – c 2 ) / (2 • a • b)

Получив cos(γ) угла, далее через функцию

arccos узнаём сколько это будет в градусах: arccos (cos(γ)) = угол.

Т.е. по примеру это: (1000 2 + 1000 2 – 1500 2 ) / (2 • 1000 • 1000) = -0.125 отсюда arccos (-0.125)= 97.18 градусов.

Теги: #Как высчитать градусы угла

Угол.

Градусная мера угла.

• Альфашкола
• Статьи
• Угол

Понятие угла является одним из наиболее важных определений в геометрии.  У́гол  — геометрическая фигура, образованная двумя лучами, сторонами угла, выходящими из одной точки, которая называется вершиной угла. Понятия равенства и суммы углов часто используется в  тригонометрии. Например, углы \(15,30,45\) градусов.

Наиболее распространенными единицами измерения угла являются градус и радиан. Один градус —  это «\(\frac{1}{360}\)» полного круга. \(90\) градусов — это четверть круга, \(180\) – половина круга, \(270\) — три четверти круга и \(360\) это целый круг. Прямой угол равен \(90\) градусов, острый угол больше \(0\) и меньше \(90\) градусов и тупой угол  больше \(90\) градусов и  меньше \(180\) градусов.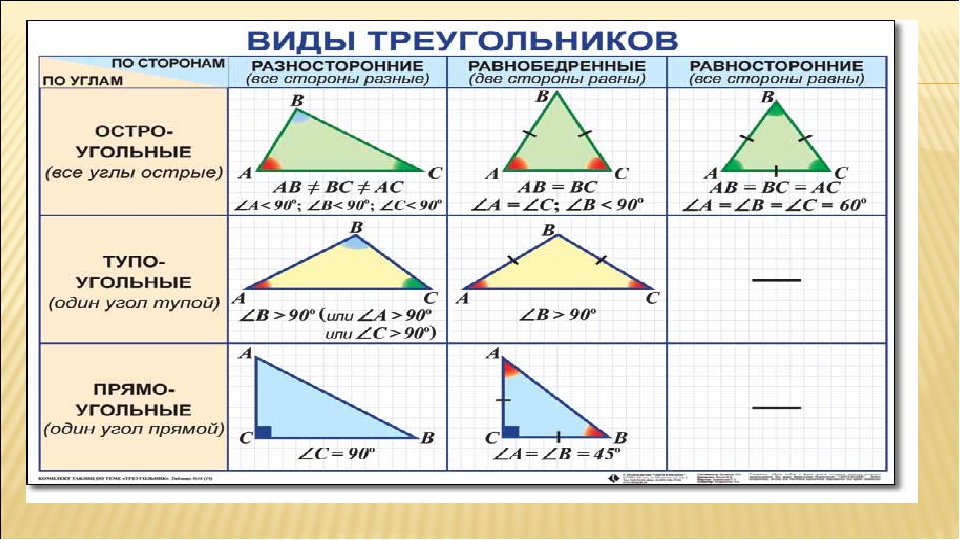 Развернутый угол равен  \(180\) градусам.

Мы изучаем углы от \(0\)° до \(360\)°, но есть углы больше \(360\)° и отрицательные углы.

Градусы могут быть разделены на минуты и секунды. Каждый градус делится на \(60\) равных частей, которые называются минутами. Так семь с половиной градусов можно сказать \(7\) градусов и \(30\) минут и записать \(7\) ° \(30\)’. Каждая минута делится на \(60\) равных частей, каждая из которых равна одной секунде. Например, \(2\) градуса \(5\) минут \(30\) секунд записывается \(2\)° \(5\)’ \(30\)». Деление градуса на минуты и секунды  аналогично делению часа на минуты и секунды времени.

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Эмма Акоповна Акопян

Репетитор по математике

Стаж (лет)

Образование:

Пятигорский государственный институт иностранных языков

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Надежда Геннадьевна Зубкова

Репетитор по математике

Стаж (лет)

Образование:

Астраханский педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Ирина Владимировна Милёшина

Репетитор по математике

Стаж (лет)

Образование:

Куйбышевский государственный педагогический институт

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Репетитор по алгебре
• Репетитор по химии для подготовки к ЕГЭ
• Репетитор для подготовки к ЕГЭ по физике
• Репетитор по грамматике русского языка
• ВПР по математике
• ВПР по физике
• Репетитор для подготовки к ВПР по обществознанию
• Репетитор по географии для подготовки к ЕГЭ
• Репетитор по информатике для подготовки к ОГЭ
• Scratch

Похожие статьи

• Объем и площадь параллелепипеда
• МИФИ: Программная инженерия
• МФТИ: факультеты и специальности, проходной балл, вступительные испытания
• ЕГЭ по математике, базовый уровень. Задачи на исследование функций (вариант 4)
• Как школьнику выстроить идеальные отношения с родителями
• Что делать, если школьник придумывает истории и жалуется родителям на преподавателя?
• Что такое новогодний адвент-календарь, как его сделать и зачем он нужен?
• Новогодние блюда, которые подойдут детям и тем, кто на диете

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Как рассчитать угол в градусах?

Угол измеряется в градусах (°) и радианах. Он образуется между двумя соседними сторонами многоугольника. Каждый многоугольник имеет разные стороны и разное количество углов.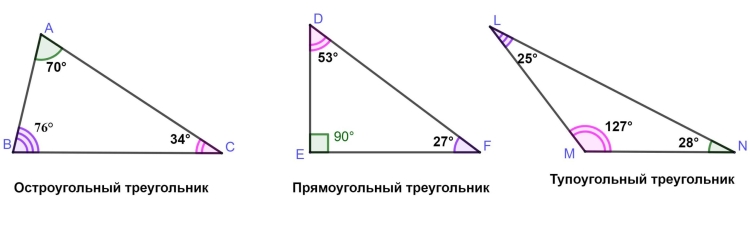 Формула для нахождения углов в градусах полезна в геометрии и тригонометрии. Важно понимать другие понятия математики, такие как дуга, центральный угол окружности и т. д.  

1. Полный круг = 360°
2. Прямая линия = 180°
3. Полуокружность = 180°
4. Четверть окружности = 90°

Вычисление углов в градусах

Существует три различных метода нахождения углов в градусах:

1. Использование протектора D
2. Теорема Пифагора и тригонометрическая функция в прямоугольном треугольнике  
3. Использование формулы суммы углов
4. Центральный угол окружности

Использование протектора D

сантиметры или миллиметры. Протектор, используемый для измерения углов, имеет форму буквы «D» со значением угла, отмеченным от 0 до 180 ° в любом направлении (вправо или влево). Нам нужно выровнять ось с линией на D, чтобы измерить угол. Средняя окружность протектора совмещена с вершиной измеряемого угла. Лучи, проходящие через вершину угла, помогут найти угол в градусах.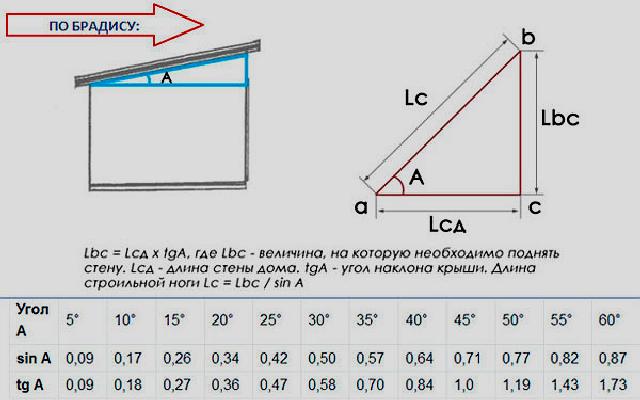

Использование теоремы Пифагора и тригонометрической функции в прямоугольном треугольнике  

В тригонометрии есть шесть функций: синус, кос, косек, тангенс, кот, и сек. Прямоугольный треугольник имеет три стороны, основание, перпендикуляр и гипотенузу.

• Основание: Сторона, примыкающая к углу 90°.
• Перпендикуляр: Также является прилежащей стороной к углу 90°.
• Гипотенуза: Сторона, противоположная углу 90°.

Прямоугольный треугольник представлен углом 90° как одним из углов. Сумма всех углов треугольника равна 180°.

• Cosecθ: Представляется гипотенузой, деленной перпендикуляром.

Cosecθ =

• Cotθ: Представляется как основание, разделенное перпендикуляром.

Cotθ =

Остальные тригонометрические функции представлены как:

sinθ =

cosθ =

tanθ =

secθ =

cosecθ также может быть представлен как 1/ sinθ

Secθ также может быть представлен как 1/ cosθ

Cotθ также может быть представлен как 1/ tanθ

Где,

Θ угол  

Теорема Пифагора

Если известны две стороны прямого угла, мы можем легко вычислить третью сторону прямоугольного треугольника.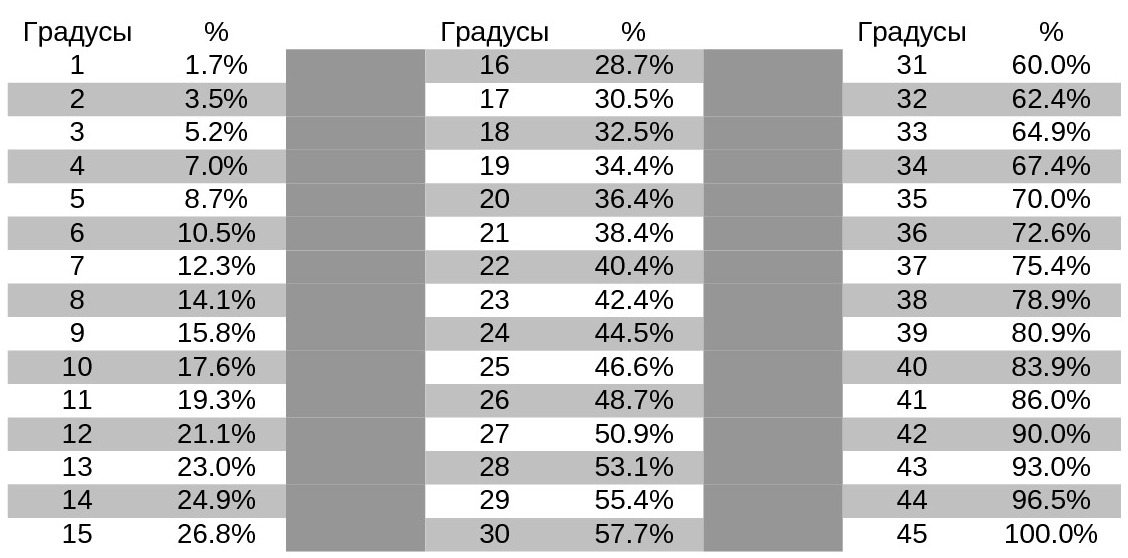 В прямоугольном треугольнике теорема Пифагора дается формулой:

(гипотенуза) ² = (основание) ² + (перпендикуляр) ²

Формула суммы углов, образующих сумму внутренних углов многоугольника

между двумя сторонами. Если у многоугольника шесть сторон, то и углов примерно шесть. Это помогает найти угол, если известны другие углы и сумма углов многоугольника.

Формула для нахождения суммы углов многоугольника:

Общая сумма углов = 180 (n — 2)

Где,

N — количество сторон полигона

Пример:

• , если n = 4,

5

9

Сумма углов = 180 (4 – 2)

= 180 (2)

= 360°

Если n = 5,

Сумма углов = 180 (5 – 2)

= 3)

= 540°

• Если n = 6

Сумма углов = 180 (6 – 2)

= 180 (4)

= 720°

Центральный угол окружности точка.

Расстояние между центральной точкой и границей называется радиусом окружности. Угол, образованный двумя радиусами окружности, называется центральным углом. Значение центрального угла окружности лежит в пределах от 0 до 360 градусов.

Формула для расчета центрального угла окружности:

Длина дуги = 2πr × (θ/360)

Θ = 360L/2πr

Где

r — радиус окружности

AB — дуга

Тета — угол в градусах.

L = длина дуги  

Примеры задач

Вопрос 1. Найдите центральный угол окружности радиусом 2 м с длиной дуги 4 м?

Решение : 

Формула для расчета центрального угла окружности:

Θ = 360L/2πr

Где

r — радиус окружности

Тета — угол в градусах.

L = длина дуги

Θ = угол в градусах

r = 2 м

L = 4 м

Θ = 360 × 4 /2× π × 2

Θ = 190,6 центрального угла 0° окружность 114,6°.

Вопрос 2: Найдите центральный угол окружности радиусом 10см с длиной дуги 18см?

Решение :

Формула для расчета центрального угла окружности: в градусах.

L = Длина дуги

R = 10 см

L = 18 см

θ = угол в градусах

θ = 360 × 18 /2 × π × 10

θ = 103.13 °

Таким образом окружность 103,13°.

Вопрос 3: Найдите угол параллелограмма, если три других угла равны 80°, 95° и 105°?

Решение : 

В параллелограмме четыре стороны с суммой углов 360°.

Формула для нахождения суммы углов = 180 (n – 2)

Где

n количество сторон многоугольника

Здесь n = 4,

Сумма углов = 180 (4 – 2)

= 180 (2)

= 360°

Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4

360 = 80+ 95+ 105+ Угол 4

360 = 280 + Угол 4

Угол 4 = 360 – 280

Угол 9 °

Вопрос 4: Найдите угол А на данном рисунке.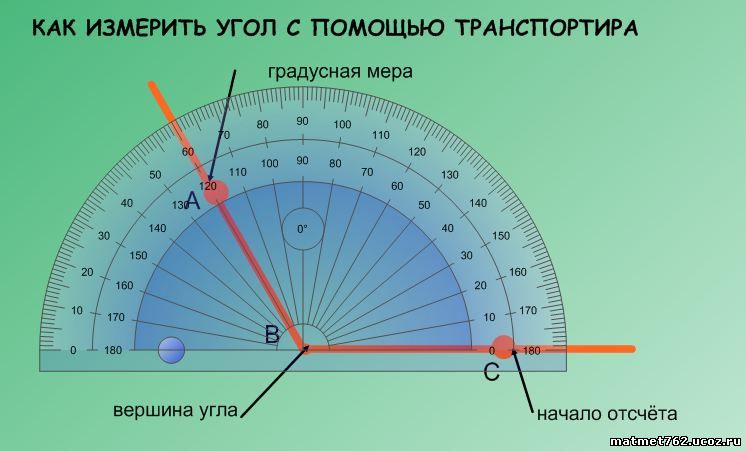

Решение :

Дано: Гипотенуза = 12

Перпендикуляр = 6

Тригонометрическая функция для вычисления угла определяется как:

2 sinA

03

A = 30°

Вопрос 5: Найдите угол A на данном рисунке.

Решение :

Дано: Гипотеновая

Вопрос 6: Найдите угол пятиугольника, если остальные четыре угла равны 115°, 100°, 105° и 100°?

Решение : 

В пятиугольнике пять сторон с суммой углов 540°.

Формула для нахождения суммы углов = 180 (n – 2)

Где

n – количество сторон многоугольника

Здесь n = 5,

Сумма углов = 180 (5 – 2)

= 180 (3)

= 540°

Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4 + Угол 5

540 = 115° + 100° + 105°+100° + Угол 5

540 = 420 + Угол 5

Угол 5 = 540 – 420

Угол 5 = 120°

Вопрос 7: Найдите угол A на данном рисунке.

Решение :

Дано: База = √3

Перпендикуляр = 1

Функция тригонометрии для расчета угла задается:

=

= 1/√3

. A = 30°

Вопрос 8. Найдите угол параллелограмма, если три других угла равны 100°, 70° и 80°?

Решение :

У параллелограмма четыре стороны с суммой углов 360°.

Формула для нахождения суммы углов = 180 (n – 2)

Где

n – количество сторон многоугольника

Здесь n = 4,

Сумма углов = 180 (4 – 2)

= 180 (2)

= 360°

Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4

360 = 100 + 70 + 80 + Угол 4

Угол 4 = 360 – 250

Угол 4 = 110°

Таким образом, второй угол равен 110°.

Вопрос 9: Найдите угол шестиугольника, если остальные пять углов равны 120°, 115°, 110°, 125° и 105°?

Решение : 

В шестиугольнике шесть сторон с суммой углов 720°.

Формула для нахождения суммы углов = 180 (6 – 2)

Где,

n – количество сторон многоугольника

Здесь, n = 6,

Общая сумма углов = 180 (6 – 2)

= 180 (4)

= 720°

Общая сумма = Угол 1 + Угол 2 + Угол 3 + Угол 4 + Угол 5 + Угол 6

720 = 120 + 115 + 110 + 125 + 105 + Угол 6

720 = 575 + Угол 6

Угол 6 = 720 – 575

Угол 6 = 0002°, шестиугольника составляет 145°.

Как рассчитать угол в градусах

••• joxxxxjo/iStock/GettyImages

Обновлено 13 марта 2018 г.

Автор Susan Revermann

Углы и вычисление градусов являются основополагающими понятиями в геометрии и тригонометрии, но эти знания также полезны в таких областях, как астрономия, архитектура и инженерия. Умение находить градусы угла — необходимый навык, которым вы должны овладеть, прежде чем углубляться в более сложные понятия, такие как радианы, длина дуги и площадь сектора. В зависимости от уровня математики, на котором вы находитесь, и конкретного угла, с которым вы имеете дело, вы можете вычислить градусы угла несколькими различными методами.

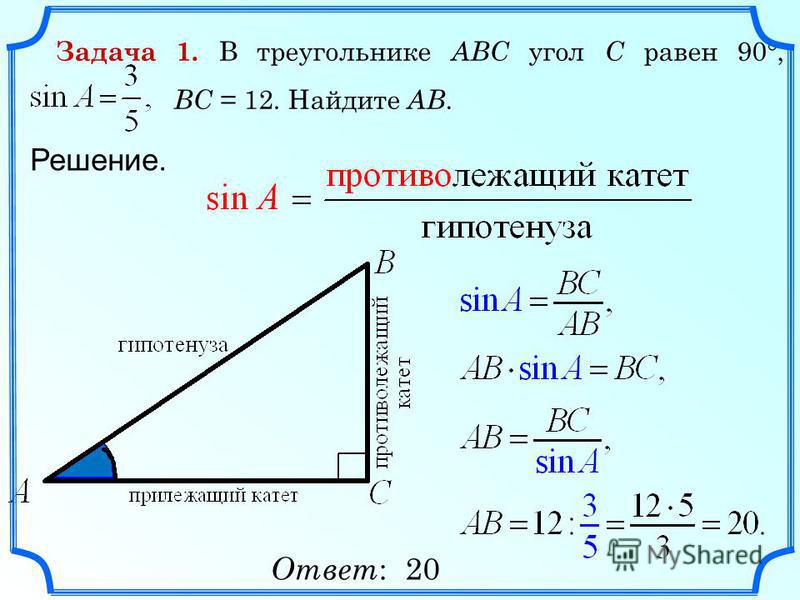
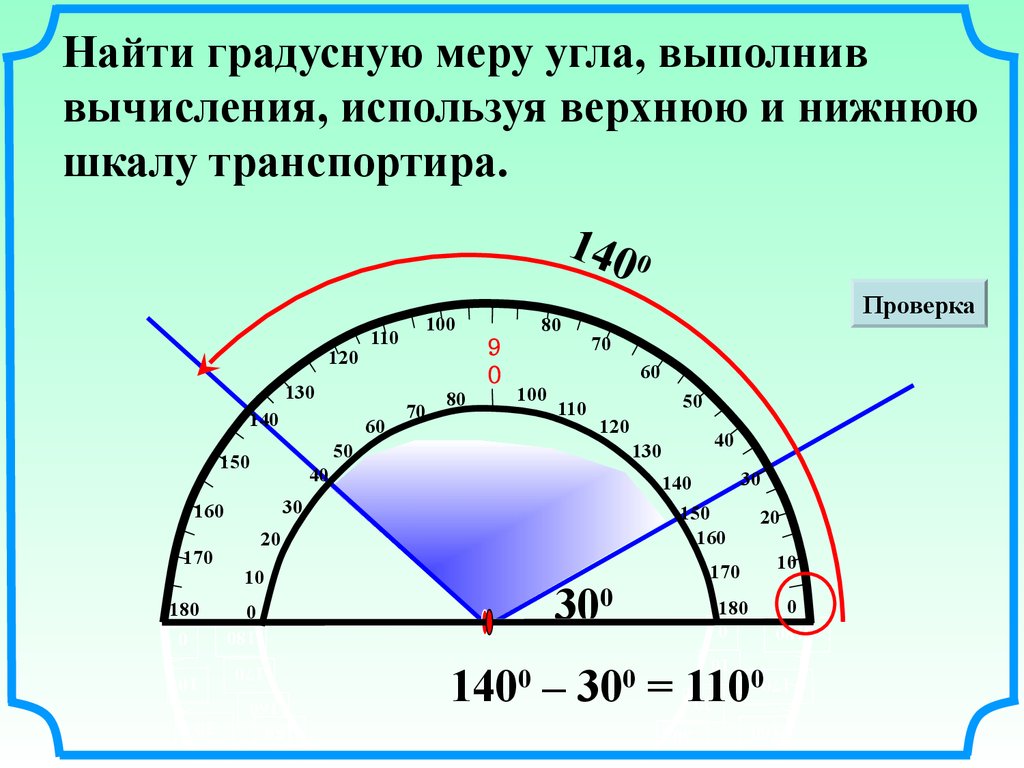
Использование транспортира

Транспортир используется для измерения углов так же, как линейка для измерения длины. Это пластиковый или металлический полукруг с градациями через равные промежутки времени от 0 до 90 градусов вправо и влево от нулевого положения. Он прост в использовании: совместите градацию «0» на транспортире с одним из лучей угла и расположите средний круг на транспортире на вершине угла. Обратите внимание, где другой луч угла совпадает с транспортиром — это даст вам градусы угла.

Треугольники предсказуемы

Треугольник всегда имеет три угла, и их сумма всегда равна 180 градусам. Зная это, всегда можно вычислить значение одного из углов, если известны значения двух других. Просто сложите эти два значения и вычтите из 180. Однако это не поможет, если вы не знаете значений ни одного из углов. В таком случае может помочь тригонометрия прямоугольных треугольников.

Тригонометрия в помощь

Прямоугольный треугольник — это треугольник, содержащий 9Угол 0 градусов. Таким образом, два других угла в сумме составляют 90 градусов, поэтому, если вы сможете найти один из них, вы узнаете и другой. В любой неправильный треугольник можно вписать прямоугольный треугольник и определить один из углов по таблицам синусов и косинусов.

Значение любого угла в прямоугольном треугольнике можно определить по длинам образующих его линий, которые можно измерить. Деление длины линии, противоположной углу, на гипотенузу дает дробь, известную как «синус» угла, а деление длины линии, прилегающей к углу, на гипотенузу дает «косинус». Вы можете посмотреть обе эти дроби на диаграммах, чтобы найти угол.

Пример

У вас есть треугольник с тремя неизвестными углами. Вы проводите линию, перпендикулярную одной из линий в треугольнике, чтобы разделить один из углов пополам, таким образом образуя прямоугольный треугольник. Как только вы измерите длины линий, у вас будет все необходимое для определения значений всех углов.

Легче всего определить угол, который вы не делили пополам.