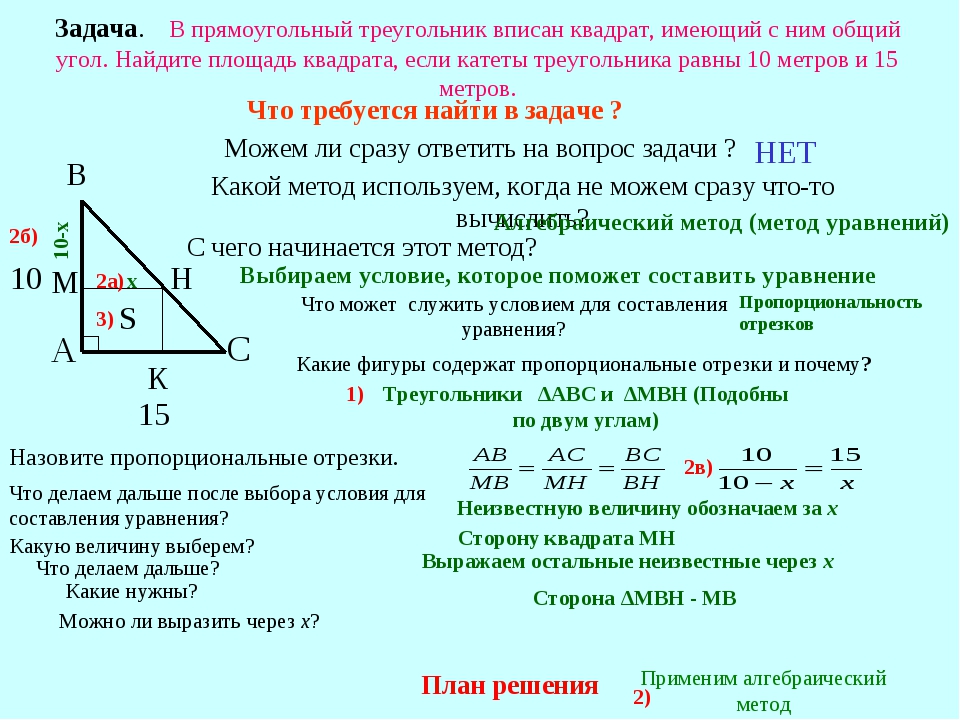
Как высчитать квадратуру треугольника: Площадь треугольника

Содержание

Площадь треугольника

Какие размеры треугольника известны:

Основание и высота Три стороны

Укажите размеры:

Площадь:

Решение:

Отправить ссылку в:

Треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

По типовым особенностям формы, треугольники бывают разносторонние, прямоугольные, равнобедренные, равносторонние.

Формула площади треугольника

Посчитать площадь треугольника можно разными способами.

Это зависит от формы треугольника и известных размеров. Так есть типовые расчёты площади для прямоугольного, равнобедренного и равностороннего треугольников.

Площадь треугольника расчитывается по размерам трёх сторон по формуле Герона или через основание и высоту треугольника.

Через основание и высоту:

S = \dfrac{1}{2} ah

S — площадь треугольника
h — высота
a — основание

По трём сторонам через полупериметр —

формула Герона:

S = \sqrt{p(p — a)(p — b)(p — c)}

p = \dfrac{a + b + c}{2}

S — площадь треугольника
p — полупериметр треугольника
a, b, c — стороны треугольника

Формулы площади треугольника

Подождите пару секунд пока подгрузятся формулы

Внимание! Десятичную дробь надо писать с точкой(. ), а не с запятой!

Через основание и высоту

$$S= \frac{1}{2} ah $$ $S$ — площадь треугольника

$a$ — основание

$h$ — высота

$a =$ $h =$

Через две стороны и угол

$$S= \frac{1}{2} ab sin \alpha $$ $S$ — площадь треугольника

$a$ — сторона

$b$ — сторона

$ \alpha $ — угол между сторонами $a$ и $b$

$a =$ $b =$ $ \alpha =$

Формула Герона

$$S= \sqrt{p(p-a)(p-b)(p-c)} $$ $S$ — площадь треугольника

$a$ — сторона

$b$ — сторона

$c$ — сторона

$p$ — полупериметр, $p= \frac{a+b+c}{2}$

$a =$ $b =$ $c =$

Через радиус вписанной окружности

$$S= rp $$ $S$ — площадь треугольника

$r$ — радиус вписанной окружности

$a$ — сторона

$b$ — сторона

$c$ — сторона

$p$ — полупериметр, $p= \frac{a+b+c}{2}$

$r =$ $p =$

Через радиус описанной окружности

$S= \frac{abc}{4R} $

$S$ — площадь треугольника

$R$ — радиус описанной окружности

$a$ — сторона

$b$ — сторона

$c$ — сторона

$a =$ $b =$

$c =$ $R =$

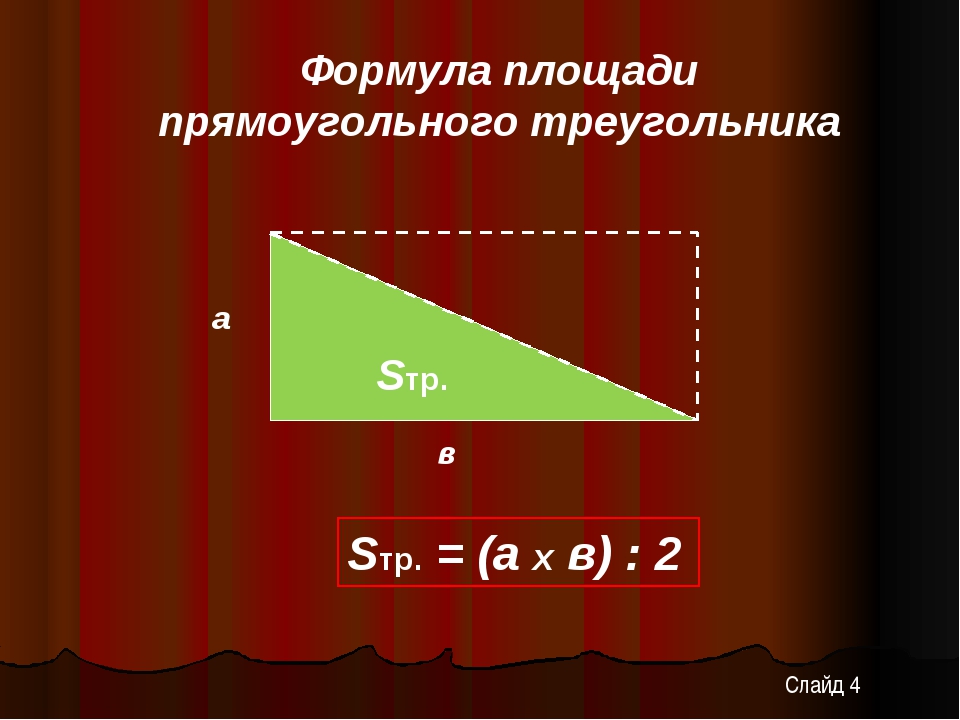
Площадь прямоугольного треугольника

$$S= \frac{1}{2} ab $$ $S$ — площадь треугольника

$a$ — сторона

$b$ — сторона

$a =$ $b =$

Площадь прямоугольного треугольника

$$S= de $$ $S$ — площадь треугольника

$d =$ $e =$

Формула Герона для прямоугольного треугольника

$$ S= (p-a)(p-b) $$ $S$ — площадь треугольника

$a$ — сторона

$b$ — сторона

$p$ — полупериметр, $p= \frac{a+b+c}{2}$

$a =$ $b =$ $p =$

Площадь равнобедренного треугольника

$$S= \frac{1}{2} a^2 sin \alpha$$ $S$ — площадь треугольника

$a$ — сторона

$\alpha$ — угол между боковыми сторонами

$a =$ $ \alpha =$

Площадь равнобедренного треугольника

$a$ — сторона

$b$ — сторона

$\alpha$ — угол между боковыми сторонами и основанием

$a =$ $b =$ $ \alpha =$

Площадь равнобедренного треугольника

$$S= \frac{b^2}{4tg \frac{ \alpha }{2}} $$ $S$ — площадь треугольника

$b$ — сторона

$\alpha$ — угол между боковыми сторонами и основанием

$b =$ $\alpha =$

Формула Герона для равнобедренного треугольника

a = b =

Площадь равностороннего треугольника

$$S= \frac{ \sqrt{3}a^2}{4} $$ $S$ — площадь треугольника

$a$ — сторона

$a =$

Площадь равностороннего треугольника

$$S= \frac{3 \sqrt{3}R^2}{4}$$ $S$ — площадь треугольника

$R$ — радиус описанной окружности

$R =$

Площадь равностороннего треугольника

$$S= 3 \sqrt{3}r^2 $$ $S$ — площадь треугольника

$r$ — радиус вписанной окружности

$r =$

Площадь равностороннего треугольника

$$S= \frac{h^2}{\sqrt{3}}$$ $S$ — площадь треугольника

$h$ — высота

$h =$

Расчет периметра и площади треугольника

Треугольник имеет три угла или вершины, и три стороны, которые являются прямыми отрезками.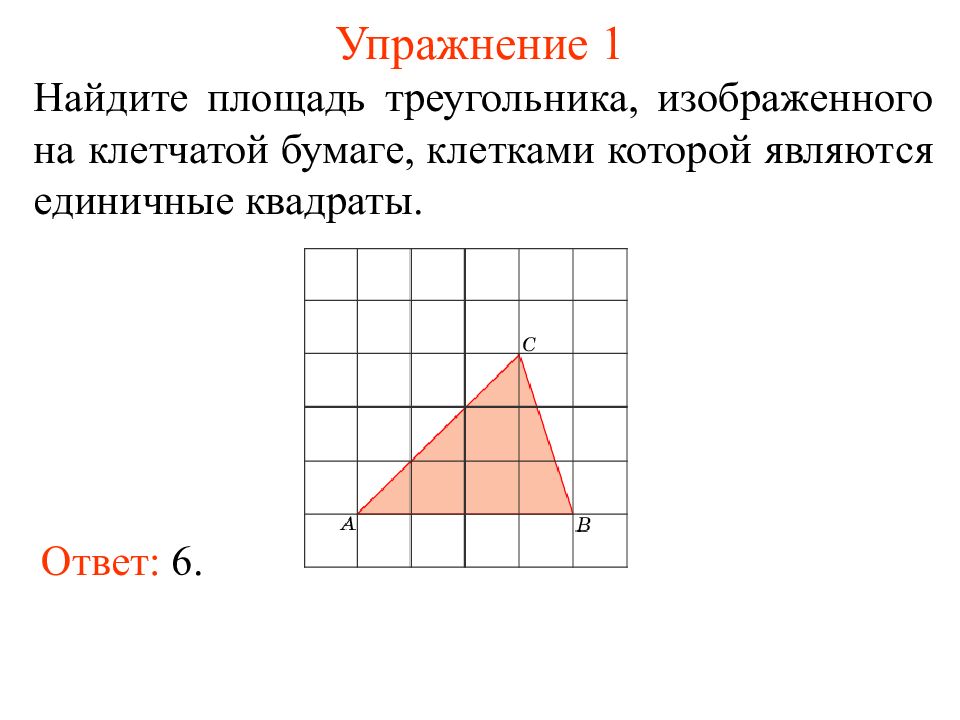

Равносторонним треугольником является треугольник, который имеет равную длину всех трех сторон.

Если две стороны треугольника и два прилегающих к ним угла равны между собой — такой треугольник называется равнобедренным

Площадь треугольника через основание и высоту: a×h/2

Периметр треугольника: (a + b + c)

Площадь равностороннего треугольника: (√(3)/4)×a²

Площадь равнобедренного треугольника(2 стороны и угол): ½×a×b×SinC

Формулы площади треугольника:

Площадь треугольника = a * h/2
Периметр треугольника = a + b + c
Площадь равностороннего треугольника = (√(3) / 4) * a²
Площадь равнобедренного треугольника = ½ * a * b * SinC

где,

h — высота треугольника,
a, b, c = стороны треугольника

Примеры :

Задача 1: Найдите площадь треугольника у которого высота = 3, а длина основания = 4.
Шаг 1: Найдем площадь.
Площадь = h * b/2 = 3 * 4/2 = 12/2 = 6.

Задача 2: Найдите периметр треугольника, если известна длина его трех сторон = 1, 2, 3.

Шаг 1: Найдем периметр.
Периметр = a + b + c = 1 + 2 + 3 = 6.

Задача 3: Найдите площадь равностороннего треугольника, если длина его стороны равна 3.

Шаг 1: Найдем площадь.
Площадь = (√(3) / 4) * a² = (1.73 / 4) * 3² = 0.43 * 9 = 3.87.

Задача 4: Найдите площадь равнобедренного треугольника если сторона его равна 3, основание = 4 и угол между ними 28.

Шаг 1: Найдем площадь.
Площадь = ½ * a * b * SinC = 0.5 * 3 * 4 * Sin(28) = 6 * 0.27 = 1.62.

Приведенные выше примеры показывают, как вычислить площадь и периметр треугольника, равностороннего треугольника,
равнобедренного треугольника вручную.

Площадь треугольника

Ниже приведены формулы нахождения площади произвольного треугольника которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров.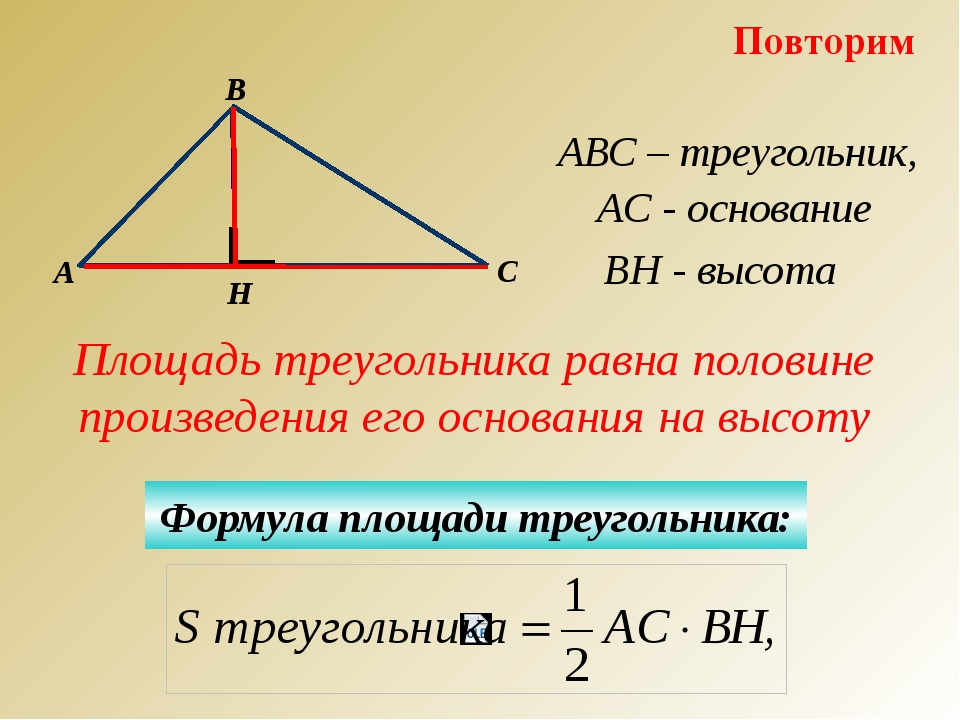 Формулы представлены в виде картинки, здесь же приведены пояснения по применению или обоснованию их правильности. Также на отдельном рисунке указаны соответствия буквенных обозначений в формулах и графических обозначений на чертеже.

Примечание. Если же треугольник обладает особыми свойствами (равнобедренный, прямоугольный, равносторонний), можно использовать формулы, приведенные ниже, а также дополнительно специальные, верные только для треугольников с данными свойствами, формулы:

Формулы площади треугольника

Пояснения к формулам:
a, b, c — длины сторон треугольника, площадь которого мы хотим найти
r — радиус вписанной в треугольник окружности
R — радиус описанной вокруг треугольника окружности
h — высота треугольника, опущенная на сторону
p — полупериметр треугольника, 1/2 суммы его сторон (периметра)
α — угол, противолежащий стороне a треугольника
β — угол, противолежащий стороне b треугольника
γ — угол, противолежащий стороне c треугольника
h_a,h_b_, h_c— высота треугольника, опущенная на сторону a, b, c

Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.

Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2 ) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу

Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)
Формула Герона (6) — это представление той же самой формулы без использования понятия полупериметра, только через длины сторон

Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов. (Формула 8)
Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
Формула 11 позволяет вычислить площадь треугольника по координатам его вершин, которые заданы в виде значений (x;y) для каждой из вершин. Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений

См. также площадь равнобедренного треугольника.

Примечание. Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет — пишите об этом в форуме. В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Иногда для простых подкоренных выражений может использоваться символ √

Задача. Найти площадь по двум сторонам и углу между ними

Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника.

Решение.

Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ

Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60

В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов. Он будет равен корню из трех на два.
S = 15 √3 / 2

Ответ

: 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)

Задача. Найти площадь равностороннего треугольника

Найти площадь равностороннего треугольника со стороной 3см.

Решение.

Площадь треугольника можно найти по формуле Герона:

S = 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )

Поскольку a = b = c формула площади равностороннего треугольника примет вид:

S = √3 / 4 * a²

S = √3 / 4 * 3²

S = 9 √3 / 4

Ответ: 9 √3 / 4.

Задача. Изменение площади при изменении длины сторон

Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?

Решение.

Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.

Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.

Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:

S = 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
(см. первую строку рисунка внизу)

Длины сторон произвольного треугольника заданы переменными a, b, c.

Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:

S₂ = 1/4 sqrt( ( 4a + 4b + 4c)(4b + 4c — 4a)(4a + 4c — 4b)(4a + 4b -4c) )
(см. вторую строку на рисунке внизу)

Как видно, 4 — общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда

S₂ = 1/4 sqrt( 4 * 4 * 4 * 4 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — на третьей строке рисунка
S₂ = 1/4 sqrt( 256 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — четвертая строка

Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня
S₂ = 16 * 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
S₂ = 4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
(см. пятую строку рисунка внизу)

Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.

S₂ / S = 16
(см. внизу подробнее запись в виде дроби и ее сокращения — в последней строке)

На рисунке логика вычисления решения, описанного выше, приведена уже в виде формул (одна за другой)

Ответ: Площадь треугольника увеличится в 16 раз

Сумма углов треугольника | Описание курса | Медиана треугольника

Площадь равнобедренного треугольника — формула, пример расчета, калькулятор

Равнобедренным треугольником называется фигура с двумя равными сторонами. В этом случае третья сторона считается основанием, а равные стороны – боковыми.

Если все стороны треугольника равны, то он считается правильным. Правильный треугольник также является равнобедренным.
Равнобедренный треугольник отличается следующими свойствами:

Углы (α) при основании равны;
Биссектрисы, медианы и высоты, исходящие из этих углов также равны между собой;
Центры описанной и вписанной окружности лежат на одной прямой;
Биссектриса, медиана и высота, проведенные из угла β к основанию b, равны между собой.

Существует множество способов нахождения площади равнобедренного треугольника. Для начала рассмотрим классический метод, для которого потребуется высота и основание. Зная эти параметры можно применить формулу площади равнобедренного треугольника:

То есть площадь равнобедренного треугольника равняется произведению высоты на половину длины основания.

Рассмотрим пример расчета площади равнобедренного треугольника.
Задача: дан треугольник, в котором основание равно 4 см, а высота 6 см. Найдите площадь.
Подставляем данные в формулу:

Площадь треугольника равняется 12 кв. см

Также найти площадь можно по формуле площади через три стороны, или как еще говорят – формуле Герона. Во многих случаях это значение находится через радиус вписанной окружности.
Найти площадь фигуры через стороны, применив метод Герона, можно по этой формуле.

Это выражение можно преобразовать в сокращенную формулу:

Рассмотрим на примере.
В равнобедренном треугольнике основание b= 3 см, а сторона a= 6 см.

Подставим значения в формулу:
или
Зная стороны, мы легко определили, что S = 8,7 кв. см

Для вычислений можно использовать две равные стороны и угол между ними.

И снова смотрим пример:
Стороны a = 6 см., а угол между ними 45°. По таблице синусов синус 45° равен 0.7071.
Рассчитываем площадь:
Площадь такого равнобедренного треугольника будет равна 12,6 квадратных сантиметра

Площадь треугольника – прямоугольного или равнобедренного, формула

Необходимость вычисления площади различных фигур, в том числе и треугольных, возникла за несколько веков до нашей эры. Над этим задумывались ученые и астрономы Древнем Египте.

В жизни иногда встречаются ситуации, когда требуется искать в закромах памяти знания из далеких школьных лет: подошла очередь ремонта в доме и нужно рассчитать количество необходимого материала, или потребовалось узнать площадь земельного участка в виде треугольника.

Вычисление площадей в Древнем Египте

Человеческая память не может сразу воспроизвести убранные за ненадобностью школьные знания, что вполне естественно.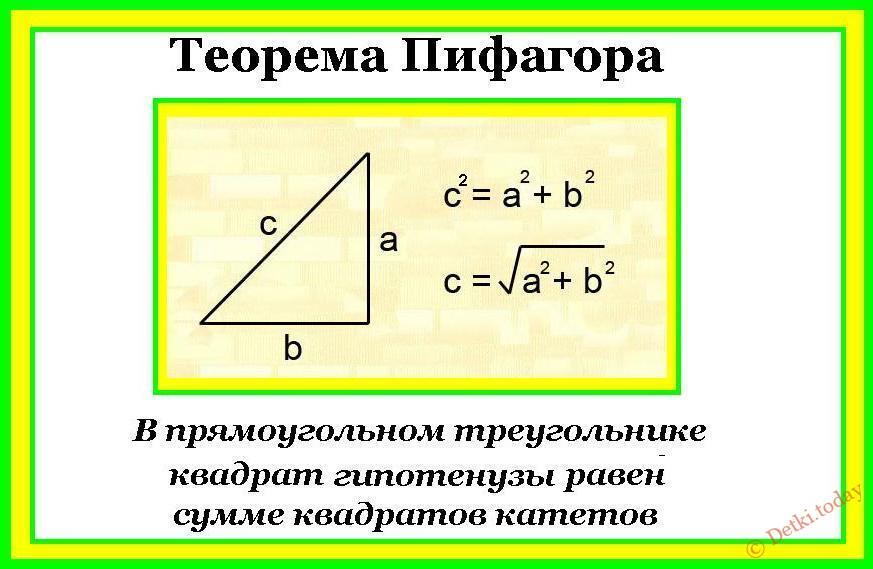 Поэтому здесь собраны основные методы для расчета площади большинства видов треугольника.

Вычислить площадь треугольника можно различными вариантами, применяя определенные формулы. Методы расчета зависят от типов треугольных фигур и от того, какие вычислительные данные известны.

Треугольник: определение и виды фигуры

Из курса геометрии известно, что треугольник представляет собой многоугольную фигуру, которая имеет три лежащие на разных линиях точки, соединенные между собой отрезками. Размер площади треугольника выражается количеством заключенных в ней квадратных единиц и представляет собой положительное число, которое показывает размер фигуры, в части поверхности, ограниченной тремя отрезками в замкнутый контур.

Треугольник

В зависимости от длины сторон и величины угла выделяется несколько разновидностей треугольников:

прямоугольный, имеющий один прямой угол;
остроугольный, все углы которого острые, то есть меньше 90 градусов;
тупоугольный, содержащий один тупой угол в диапазоне от 90 до 180 градусов;
равнобедренный, имеющий две равные по длине боковые стороны;
равносторонний, у которого все три стороны имеют одинаковое значение.

Для расчета площади каждого типа треугольной фигуры используется специальная формула.

Как вычислить площадь треугольника?

Классические формулы расчета площади треугольных фигур соотносятся с видами треугольников. Приведенные ниже формулы определения площади произвольного треугольника подойдут для установления площади, вне зависимости от его характеристик, углов или размеров.

Прямоугольный треугольник

Прямоугольный треугольник характеризуется наличием прямого угла. Две его стороны, образующие этот угол носят название катетов. Противоположная прямому углу сторона треугольника именуется гипотенузой.

Прямоугольный треугольник

Основная формула расчета площади прямоугольного треугольника основывается на значениях катетов фигуры.

Формула:

где a, b – катеты треугольника.

Расчет:

Перемножаются величины двух катетов.
Полученное значение делится на два.

Вычислить площадь прямоугольного треугольника можно по другой формуле, где за основу берется величина гипотенузы и высота, проведенная к ней.

Формула:

где c – гипотенуза, hc – высота, проведенная к гипотенузе.

Расчет:

Умножается длина гипотенуза на величину высоты, идущей от противоположной вершины.
Полученное значение уменьшается вдвое.

Равнобедренный треугольник

В равнобедренном треугольнике две боковые стороны равны по значению, отличающаяся размерами сторона называется основанием.

Равнобедренный треугольник

Площадь равнобедренного треугольника рассчитывается по формуле:

где а – равные стороны треугольника, b – основание.

Расчет:

Определяется разница из четырехкратного квадратного корня равных сторон и квадратного корня основания.
Из полученного значения извлекается квадратный корень.
Результат умножается на величину основания, уменьшенную в 4 раза.

Равносторонний треугольник

Частным случаем равнобедренного треугольника является равносторонний, отличающийся тем, что все стороны и углы фигуры равны по значению.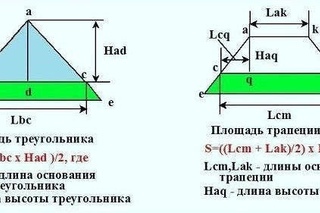

Равносторонний треугольник

Площадь равностороннего треугольника определяется по формуле:

где a – сторона равностороннего треугольника.

Определение площади треугольника с неизвестными данными

Классические формулы расчета площади треугольника могут выручить не всегда. Существует ряд ситуаций, когда неизвестны необходимые для подстановки в формулу величины. При этом используют другие методы для расчета площади треугольника, напрямую зависящие от того, какие данные известны. Все варианты предусматривают конкретную формулу и определенный порядок проведения расчетов.

Известны основание и высота

Площадь треугольника определяется как половина произведения высоты фигуры и длины основания, то есть той стороны треугольника, к которой проведена высота.

Формула:

где b – длина основания; h – высота.

Расчет:

Умножается высота на длину основания, получается площадь многоугольника.
Для получения площади треугольника полученный результат делится на 2.

Известны величины трех сторон

Площадь треугольника рассчитывается по формуле Герона. Для облегчения формулы метод предусматривает предварительный расчет величины полупериметра.

Формула Герона:

где p – величина полупериметра; a, b, c – значения длины сторон треугольника.

Расчет:

Вычисление полупериметра по формуле

Расчет площади фигуры по формуле Герона.

Известны две стороны и угол между ними

Площадь треугольника рассчитывается как произведение двух сторон, умноженное на синус угла, расположенного между этими сторонами. Угол – геометрическая фигура, полученная из двух лучей, исходящих из одной точки (вершины угла).

Пирамида

Формула:

где a, b – стороны треугольника, C – угол между сторонами.

Расчет:

Перемножение двух сторон.
Определение синуса угла – тригонометрической функции, в прямоугольном треугольнике равной отношению противолежащего катета к гипотенузе.
Умножение произведения двух сторон на синус угла.
Полученный результат делится пополам.

Известны одна сторона и прилежащие к ней углы

Площадь подобного треугольника равна половине квадрата известной стороны, умноженной на дробь, с числителем, выражающим произведение синусов прилежащих углов, и знаменателем, указывающим синус противолежащего угла.

Формула:

Расчет:

Рассчитывается квадрат известной стороны и делится на 2.
Перемножаются синусы прилежащих углов и делятся на синус противолежащего. Вычисляется противолежащий угол по формуле:

γ= 180°−(α+ β)

β= 180°−(α+ γ)

α= 180°−(β+ γ)

Перемножаются полученные значения.

Известны радиус вписанной окружности и полупериметр

Площадь треугольника определяется как произведение радиуса вписанной окружности на его полупериметр. Окружность называется вписанной, если имеет одну общую с многоугольником точку с каждой стороны фигуры. Центральная точка вписанной в треугольник окружности всегда располагается в точке, где пересекаются биссектрисы его внутренних углов.

Окружность, вписанная в треугольник

Формула:

S = p * r, где p – полупериметр треугольника, r – радиус вписанной окружности.

Расчет:

1. Полупериметр определяется как половина суммы всех сторон треугольника по формуле:

где a, b, c – стороны треугольника.

2. Перемножаются полупериметр треугольника и радиус вписанной окружности.

Известны радиус описанной окружности и периметр

Треугольник называется описанным вокруг окружности, если его стороны соприкасаются с кругом, а сам он находится снаружи. Площадь треугольника определяется как половина произведения периметра треугольника и радиуса описанной окружности.

Треугольник, вписанный в окружность

Формула:

где r – радиус описанной окружности, a, b, c – стороны треугольника.

Расчет:

Определяется периметр треугольника как сумма всех его сторон.
Умножается величина радиуса описанной окружности на величину периметра треугольника.
Полученный результат делится пополам.

Знание формул вычисления площади треугольника поможет при определении площади объемных фигур, в основе граней которых лежат треугольные фигуры, таких, как например, пирамида.

Площадь треугольника

Площадь треугольника. Во многих задачах по геометрии связанных с вычислением площадей используются формулы площади треугольника. Их существует несколько, здесь мы рассмотрим основные. Перечислить эти формулы было бы слишком просто и пользы ни какой. Мы разберём происхождение основных формул, тех что используются наиболее чаще.

Перед тем как ознакомиться с выводом формул обязательно посмотрите статью о площади параллелограмма. После изучения материала вы без труда сможете восстановить формулы в памяти (если вдруг они «вылетят» в нужный вам момент).

Первая формула

Диагональ параллелограмма разбивает его на два равных по площади треугольника:

Следовательно площадь треугольника будет равна половине площади параллелограмма:

Площадь треугольника формула

*То есть если нам будет известна любая сторона треугольника и высота опущенная на эту сторону, то мы всегда сможем вычислить площадь этого треугольника.

Формула вторая

Как уже было изложено в статье о площади параллелограмма формула имеет вид:

Площадь треугольника равна половине его площади, значит:

*То есть если будут известны любые две стороны в треугольнике и угол между ними, мы всегда сможем вычислить площадь такого треугольника.

Формула Герона (третья)

Данную формулу выводить сложно и вам это ни к чему. Посмотрите какая она красивая, можно сказать, что сама запоминается.

*Если даны три стороны треугольника, то по данной формуле мы всегда можем вычислить его площадь.

Формула четвёртая

где r – радиус вписанной окружности

*Если известны три стороны треугольника и радиус вписанной в него окружности, то мы всегда можем найти площадь этого треугольника.

Формула пятая

где R – радиус описанной окружности.

*Если известны три стороны треугольника и радиус описанной около него окружности, то мы всегда можем найти площадь такого треугольника.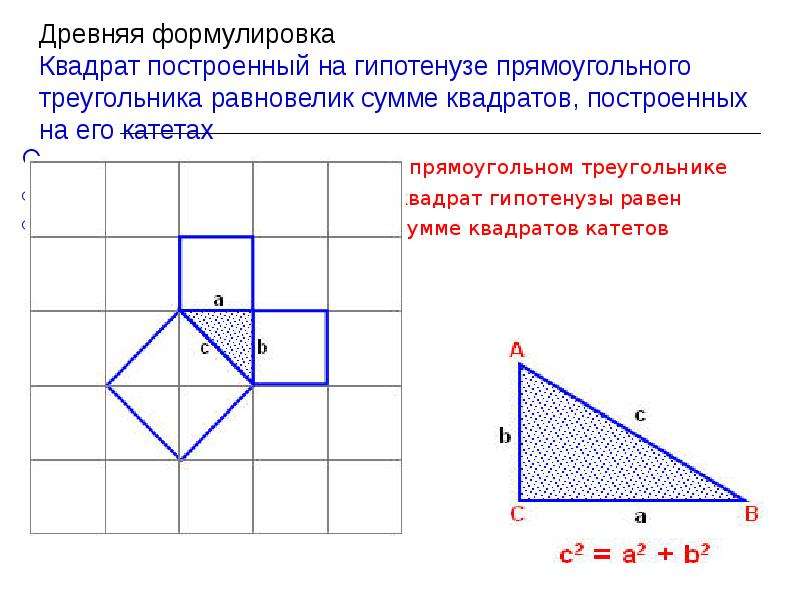

Возникает вопрос: если известны три стороны треугольника, то не проще ли его площадь найти по формуле Герона!

Да, бывает проще, но не всегда, иногда возникает сложность. Это связано с извлечением корня. Кроме того, данные формулы очень удобно применять в задачах, где дана площадь треугольника, его стороны и требуется найти радиус вписанной или описанной окружности. Такие задания имеются в составе ЕГЭ.

Давайте отдельно рассмотрим формулу:

Она является частным случаем формулы площади многоугольника, в который вписана окружность:

Рассмотрим её на примере пятиугольника:

Соединим центр окружности с вершинами данного пятиугольника и опустим из центра перпендикуляры к его сторонам. Получим пять треугольников, при чём опущенные перпендикуляры являются радиусами вписанной окружности:

Площадь пятиугольника равна:

Теперь понятно, что если речь идёт о треугольнике, то данная формула приобретает вид:

Формула шестая

Пусть сторона треугольника равна a, из противоположной вершины к этой стороне проведён произвольный отрезок образующий с ней угол (фи):

Тогда

Данная формула используется очень редко на практике, возможно вы её видите впервые, ну так просто написал, чтобы знали. Её ещё можно вывести преобразовав формулу площади четырёхугольника:

Также она является следствием из формулы:

Что добавить? Есть ещё формулы треугольника связанные с координатами вершин, векторами на которых он построен. Об этом будет статья в будущем, не пропустите!

Площадь прямоугольного треугольника. Тут всё просто — она равна половине площади прямоугольника, то есть одной второй произведения катетов.

На этом всё! Успеха Вам!

С уважением, Александр Крутицких

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

QUADRATURE_RULES_TRI — Квадратурные правила для треугольников

QUADRATURE_RULES_TRI это каталог набора данных, который содержит примеры квадратурных правил для треугольной области. Квадратурное правило — это набор из n точек (x, y) и связанных весов w , так что интеграл функции f (x, y) над треугольником T можно аппроксимировать следующим образом:

        Интеграл f (x, y) dx dy = Area (T) * Sum (1 <= i <= n) w (i) * f (x (i), y (i))

Площадь треугольника равна интегралу функции е (х, у) = 1.Это означает, что каждое полезное квадратурное правило должен удовлетворить

        Сумма (1 <= i <= n) w (i) = 1

Тот факт, что веса должны быть в сумме равными 1, дает простую проверку расчеты.

(Другие таблицы квадратурных правил для треугольников могут последовать другое соглашение, в котором сумма весов равна 1/2. Такой соглашение упрощает интегрирование по единичному треугольнику, но немного сложнее интегрировать по общему треугольнику.У меня сложилось впечатление, что сумма всех квадратурных правил должна быть равна 1, так что зависимость от площади региона обособленная и очевидная.)

Квадратурные правила для треугольника обычно определяются по T1, единичный треугольник с вершинами (0,0), (1,0), (0,1). Отсюда следует, что для интеграла по T1 имеем:

        Интеграл f (x, y) dx dy = Area (T1) * Sum (1 <= i <= n) w (i) * f (x (i), y (i))
                              = 1/2 * Sum (1 <= i <= n) w (i) * f (x (i), y (i))

Существует стандартная методика преобразования квадратурного правила если его нужно применить к общему треугольнику.

Для этого каталога квадратурное правило хранится в виде трех файлов, содержащий веса w, точки (x, y) и вершины, которые определяют треугольная область (обычно (0,0), (1,0), (0,1)).

Пример:

Вот пример квадратурного правила для единичного треугольника: порядка 6.

Вот текст X-файла, в котором хранятся абсциссы такого правила:

 
        0.6522374092 0,231933368553031
        0,6522374092 0,10903
72877
        0,231933368553031 0,6522374092
        0,231933368553031 0,10903
72877
        0,10903
72877 0,6522374092
        0,10903
72877 0,231933368553031

Вот текст файла "W", в котором хранятся веса такого правила.

 
        0,16666666666666666667
        0,16666666666666666667
        0,16666666666666666667
        0.16666666666666666667
        0,16666666666666666667
        0,16666666666666666667

которые в сумме равны 1.

Вот текст файла "R", в котором хранятся вершины треугольника:

площадь которого равна 1/2.

Лицензирование:

Компьютерный код и файлы данных, описанные и доступные на этой веб-странице распространяются по лицензия GNU LGPL.

Связанные данные и программы:

ДУНАВАН, библиотека FORTRAN90, которая определяет правила Дюнавана для квадратуры на треугольнике.

ФЕКЕТ, библиотека FORTRAN90, которая определяет правила Фекете для квадратуры или интерполяции по треугольнику.

GM_RULE, библиотека FORTRAN90, которая определяет Grundmann-Moeller правила квадратуры над треугольником, тетраэдром или общим M-мерный симплекс.

NCC_TRIANGLE, библиотека FORTRAN90, которая определяет замкнутую квадратуру Ньютона-Котеса правила на треугольнике.

NCO_TRIANGLE, библиотека FORTRAN90, которая определяет открытую квадратуру Ньютона-Котеса правила на треугольнике.

QUADRATURE_RULES_PYRAMID, каталог набора данных, который содержит квадратурные правила для пирамиды с квадратным основанием.

QUADRATURE_RULES_TET, каталог набора данных, который содержит квадратурные правила для тетраэдров, хранится в виде файла абсцисс, файла весов, и массив вершин.

QUADRATURE_RULES_WEDGE, каталог набора данных, который содержит квадратурные правила для клина (треугольник x линия).

КВАДРЕЛЬ, библиотека FORTRAN90, которая определяет различные квадратурные правила.

SIMPACK, библиотека FORTRAN77, которая аппроксимирует интеграл функции или вектор функций над многомерным симплексом или областью, которая является сумма многомерных симплексов.

ШТАНГ, библиотека FORTRAN90, которая определяет квадратурные правила для множества геометрических фигур.

TEST_TRI_INT, библиотека FORTRAN90, которая может использоваться для тестирования алгоритмов для квадратуры над треугольником.

TRIANGLE_EXACTNESS, программа FORTRAN90, которая исследует полиномиальную точность квадратурного правила для треугольника.

Образцы файлов:

CENTROID , правило центроида, порядок 1, степень точности 1.

GAUSS4X4 , порядок 16, степень точности 7, (по сути, продукт двух 4-точечных одномерных правил Гаусса-Лежандра).

GAUSS8X8 , порядок 64, точность 15, (по сути, продукт двух 8-балльных одномерных правил Гаусса-Лежандра).

SEVEN_POINT , порядок 7, степень точности 3.

STRANG1 , порядок 3, степень точности 2.

STRANG2 , порядок 3, степень точности 2.

STRANG3 , порядок 4, степень точности 3.

STRANG4 , порядок 6, степень точности 3.

STRANG5 , порядок 6, степень точности 4.

STRANG6 , порядок 7, степень точности 4.

STRANG7 , порядок 7, степень точности 5.

STRANG8 , порядок 9, степень точности 6.

STRANG9 , порядок 12, степень точности 6.

STRANG10 , порядок 13, степень точности 7.

TOMS584_19 , порядок 19, степень точности 8, правило от Алгоритм ACM TOMS # 584.

TOMS612_19 , порядок 19, степень точности 9, линейка от Алгоритм ACM TOMS №612.

TOMS612_28 , порядок 28, степень точности 11, правило от Алгоритм ACM TOMS №612.

TOMS706_37 , порядок 37, степень точности 13, правило от Алгоритм ACM TOMS №706.

VERTEX , правило вершин, порядок 3, степень точности 1.

Вы можете подняться на один уровень до страницу НАБОРЫ ДАННЫХ.2 $. Следовательно, $ \ xi_2 = \ sqrt {3} / 6 $. Резюмируя: $$ (w_1, w_2) = (\ frac {1} {2}, \ frac {1} {2}) \ quad \ mbox {и} \ quad (\ xi_1, \ xi_2) = (- \ frac {\ sqrt { 3}} {6}, + \ frac {\ sqrt {3}} {6}) $$ В культуре конечных элементов иногда используется сокращенная интеграция , что означает, что в нашем случае $ f (\ xi) $ должен быть проинтегрированным, как если бы это был только многочлен степени $ 1 $, который является линейным. В этом случае мы имеем только уравнения (1) и (2), которые должны быть выполнены: $ 1 = w_1 + w_2 $ и $ 0 = w_1. \ Xi_1 + w_2. \ Xi_2 $. Есть множество решений для это сделать.2 \ times \ begin {cases} 1/6 \\ 1/4 \\ 0 \ end {cases} $$ Вопрос: какой из них лучший? Все эти схемы интеграции на первый взгляд кажутся одинаково хорошими. На первый взгляд, потому что необходимо рассмотреть еще одну проблему: стабильность / надежность .

Следующую книгу можно загрузить из Интернета. Речь идет о методах конечного объема, но в нем также содержатся важные рекомендации для метода конечных элементов.

Сухас В. Патанкар, Численное моделирование теплопередачи и потока жидкости.2 \ раз C исключение будучи $ \, C = \ color {green} {0} $, что оказывается: интегрирование (точек) в вершинах элемента !
Это видно на следующем рисунке для нашей постоянной $ p = 100 $ и количества узлов $ N = 20 $. Обратите внимание на разные цвета:

Таким образом, мы можем заключить, что случай с $ \, \ color {red} {C = 1/4} \, $ (т.е. интегрирование центроидов) наихудший, а случай с $ \ color {green} {C = 0} $ ( т.е. интеграция вершин) лучше всего.
Коэффициенты уравнений могут сильно различаться от места к месту, особенно в задачах более высокой размерности.Так что надежность (то есть безусловная стабильность) - это не роскошь, и уж точно не в 2-D и 3-D.
Двумерный
Но это еще не все. Альтернативные схемы интеграции в FEM - это своего рода врата для включения знаний других численные методы, такие как метод конечных объемов. Как показано здесь, например: В этом ответе не упоминалось, что точки интегрирования в четырехугольном конечном элементе фактически взяты в узловых точках , т.е.е. вершины, как было предложено в вопросе OP:

В результате четырехугольник разбивается на четыре линейных треугольника:

Наконец, эти треугольники составляют эквивалентный метод конечных объемов для задачи диффузии в контексте конечных элементов. Гораздо более полное изложение этой теории можно найти в другом месте, поскольку оно слишком велико, чтобы вписаться в рамки MSE: 2-D элементарные подструктуры .
Трехмерный
Чем выше размерность, тем сложнее сформулировать лаконичный ответ.Но повсюду одна и та же история: точки интегрирования в вершинах (кирпича в трехмерном пространстве) - лучший вариант, гарантирующий безусловную устойчивость конечного элемента. схемы. При этом следует подчеркнуть, что числовые схемы не обязательно должны быть одинаковыми для разных членов частичного дифференциальное уравнение. Результатом исследования, приведенного ниже, стала публикация статьи Хорста Фихтнера, этого автора и другие. Название статьи: Продольные градиенты распределения аномальных космических лучей во внешней гелиосфере . 2 \ right) $$ где мы заметили, что подынтегральное выражение является квадратичной функцией на $ A_i $, так что стандартная квадратурная формула выборки средней точки для треугольников дает интеграл ровно .2, {x, 0, 1}, PlotStyle -> Красный, Эпилог -> {Пунктирный, Зеленый, Толщина -> 0,0005, Строка [{{1, 0}, {1, 1}, {0, 1}}], синяя, линия [{{0, 1/4}, {1, 1/4}}]}, Заливка -> 0,25, Стиль заливки -> Директива [Синий, Непрозрачность [0,38]], AxesStyle -> Arrowheads [.035], PlotRangePadding -> Scaled [.1], Соотношение сторон -> 1, AxesLabel -> (Style [#, 15, FontFamily -> «Times New Roman», курсив, Жирный] & / @ {"x", "y"})]
% PDF-1.3 % 802 0 объект > эндобдж xref 802 83 0000000016 00000 н. 0000002011 00000 н. 0000002111 00000 п. 0000002619 00000 н. 0000002849 00000 н. 0000003285 00000 н. 0000003381 00000 н. 0000004480 00000 н. 0000004752 00000 п. 0000004774 00000 н. 0000005075 00000 н. 0000005097 00000 н. 0000005974 00000 п. 0000005997 00000 н. 0000007105 00000 н. 0000007127 00000 н. 0000008115 00000 п. 0000008138 00000 п. 0000009264 00000 н. 0000009286 00000 п. 0000010227 00000 п. 0000010495 00000 п. 0000010781 00000 п. 0000010803 00000 п. 0000011802 00000 п. 0000011823 00000 п. 0000011844 00000 п. 0000011867 00000 п. 0000012960 00000 п. 0000012982 00000 п. 0000014052 00000 п. 0000014074 00000 п. 0000014987 00000 п. 0000015010 00000 п. 0000016645 00000 п. 0000016668 00000 п. 0000019394 00000 п. 0000019415 00000 п. 0000019713 00000 п. 0000019735 00000 п. 0000020771 00000 п. 0000020793 00000 п. 0000021998 00000 п. 0000022020 00000 н. 0000022848 00000 н. 0000022871 00000 п. 0000024264 00000 п. 0000024287 00000 п. 0000025793 00000 п. 0000025816 00000 п. 0000027220 00000 н. 0000027243 00000 п. 0000030093 00000 п. 0000030116 00000 п. 0000035043 00000 п. 0000035066 00000 п. 0000039223 00000 п. 0000039246 00000 п. 0000040677 00000 п. 0000040699 00000 п. 0000041473 00000 п. 0000041496 00000 п. 0000045587 00000 п. 0000045610 00000 п. 0000049546 00000 п. 0000049569 00000 п. 0000054216 00000 п. 0000054239 00000 п. 0000058437 00000 п. 0000058460 00000 п. 0000062599 00000 н. 0000062622 00000 п. 0000065792 00000 п. 0000065815 00000 п. 0000070594 00000 п. 0000070617 00000 п. 0000073406 00000 п. 0000073429 00000 п. 0000075444 00000 п. 0000075465 00000 п. 0000075756 00000 п. 0000002175 00000 н. 0000002597 00000 н. трейлер ] >> startxref 0 %% EOF 803 0 объект > эндобдж 804 0 объект > эндобдж 883 0 объект > поток Hb``pa`g`a` ؿ Ab @ ̱IIII! ΨMp? V] L [zBGGG [GT ״ 9 OM R: LZ ڌ j`
(PDF) Квадратура Гаусса Лежандра над треугольником
Дж.Индийский институт Наук, сентябрь – октябрь. 2004, 84, 183–188
© Индийский институт науки.
* Автор для переписки.
Краткое сообщение
Квадратура Гаусса Лежандра над треугольником
HT RATHOD
1
*, KV NAGARAJA
2
, B. VENKATESUDU
3
AND NL
4 0003 Отделение математики, кампус Центрального колледжа, Бангалорский университет, Бангалор 560 001, Индия.
2
Департамент математики, Технологический и научный институт Амрита, Бангалор 560 037, Индия.
3
Математический факультет Оксфордского инженерного колледжа, Бангалор 560 068, Индия.
4
Департамент математики, Технологический институт М. С. Рамая (MSRIT), Бангалор 560 068, Индия.
адреса электронной почты:
1
[email protected];
2
[email protected];
3
venkateshoxford123 @ yahoo.com;
4
[email protected]; Телефоны:
1
+ 91-80-23591441;
2
+ 91-80-26538093;
3
+ 91-80-26680523;
4
+ 91-80-23621607.
Поступило 17.11.2003 г .; Пересмотрена 06 апреля 2004 г.
Abstract
В данной статье представлен квадратурный метод Гаусса-Лежандра для численного интегрирования по стандартной треугольной поверхности
: {(x, y)
xyxy
в декартовой двумерной (x , y) пробел.Математическое преобразование
из пространства (x, y) в пространство (ξ, η) отображает стандартный треугольник в пространстве (x, y) в стандартный двумерный квадрат в пространстве (ξ, η)
: {(ξ , η) | –1 ≤ ξ, η ≤ 1}. Это преодолевает трудности, связанные с получением новых весовых коэффициентов
и точек выборки, и дает точные и надежные результаты. Результаты, полученные с новыми формулами
, сравниваются с существующими формулами.
Ключевые слова: метод конечных элементов, численное интегрирование, квадратура Гаусса Лежандра, треугольные элементы, стандарт
2-квадрат, расширенное численное интегрирование.
1. Введение
В последние годы метод конечных элементов (МКЭ) стал очень мощным инструментом для приближенного решения
краевых задач, управляющих различными физическими явлениями.
Его широко используют в промышленности и исследованиях, и без него многие практические проблемы в науке и технике не могут быть решены. Треугольные элементы с прямыми или изогнутыми сторонами
очень широко используются в конечно-элементном анализе.Универсальность
этих треугольных элементов может быть дополнительно увеличена за счет улучшенного численного интегрирования схем
. В FEM различные интегралы должны определяться численно при оценке
матрицы жесткости, матрицы масс, вектора объемной силы и т. Д.
Основная проблема интегрирования произвольной функции двух переменных по поверхности треугольника
заключалась в следующем. впервые дано Хаммером и др. [1] и Хаммер и Страуд [2, 3]. С появлением
метода конечных элементов треугольные элементы оказались универсальными.Значительный интерес вызывает
схем численного интегрирования по треугольникам. Каупер [4]
предоставил таблицу квадратурных формул Гаусса для симметрично расположенных точек интегрирования.
Симметричные квадратурные правила для треугольников.
TRIANGLE_SYMQ_RULE - Симметричные квадратурные правила для треугольников.
TRIANGLE_SYMQ_RULE это библиотека C ++, которая возвращает симметричные квадратурные правила, с точностью до общей степени 50, над внутренностью произвольного треугольника в 2D, Хун Сяо и Жидрунас Гимбутас.
Исходный исходный код, из которого была разработана эта библиотека, можно получить в Лаборатории математики и вычислений Куранта по адресу: http://www.cims.nyu.edu/cmcl/quadratures/quadratures.html,
Лицензирование:
Компьютерный код и файлы данных, доступные на этом веб-страницы распространяются под лицензия GNU LGPL.
Языки:
TRIANGLE_SYMQ_RULE доступен в версия C и версия C ++ и версия FORTRAN90 и версия MATLAB.
Связанные данные и программы:
ANNULUS_RULE, библиотека C ++, которая вычисляет квадратурное правило для оценки интегралов функции над внутренней частью кругового кольца в 2D.
CUBE_FELIPPA_RULE, библиотека C ++, которая возвращает точки и веса квадратурного правила Фелиппа над внутренней частью куба в 3D.
ГНУПЛОТ, Программы на C ++, которые проиллюстрировать, как программа может записывать данные и командные файлы так что gnuplot может создавать графики результатов программы.
PYRAMID_FELIPPA_RULE, библиотека C ++, которая возвращает квадратурные правила Фелиппы для аппроксимации интегралов над внутренней частью пирамиды в 3D.
SIMPLEX_GM_RULE, библиотека C ++, которая определяет квадратурные правила Грундмана-Меллера над внутренней частью симплекса в размерах M.
SQUARE_FELIPPA_RULE, библиотека C ++, которая возвращает точки и веса квадратурного правила Фелиппа над внутренней частью квадрата в 2D.
SQUARE_SYMQ_RULE, библиотека C ++, которая возвращает симметричные квадратурные правила, с точностью до общей степени 20, над внутренней частью симметричного квадрата в 2D, Хун Сяо и Жидрунас Гимбутас.
ШТАНГ, библиотека C ++, которая определяет квадратурные правила для множества M-мерных областей, включая внутреннюю часть квадрата, куба и гиперкуба, пирамиды, конус и эллипс, шестиугольник, М-мерный октаэдр, круг, сфера и гиперсфера, треугольник, тетраэдр и симплекс, и поверхность круга, сферы и гиперсферы.
TETRAHEDRON_FELIPPA_RULE, библиотека C ++, которая возвращает квадратурные правила Фелиппы для аппроксимации интегралов над внутренней частью тетраэдра в 3D.
TOMS886, г. библиотека C ++, которая определяет точки Падуи для интерполяции в 2D области, включая прямоугольник, треугольник и эллипс, Марко Калиари, Стефано де Марчи, Марко Вианелло. Это версия алгоритма 886 ACM TOMS.
TRIANGLE_ANALYZE, программа на C ++, которая считывает треугольник, определенный в файле, и использует функцию triangle_properties () библиотека для вычисления углов, площади, центроида, описанной окружности, длин ребер, вписанная окружность, ориентация, ортоцентр и качество.
TRIANGLE_DUNAVANT_RULE, библиотека C ++, которая определяет правила Дюнавана для квадратуры над внутренней частью треугольника в 2D.
TRIANGLE_FEKETE_RULE, библиотека C ++, которая определяет правила Фекете для интерполяции или квадратуры над внутренней частью треугольника в 2D.
TRIANGLE_FELIPPA_RULE, библиотека C ++, которая возвращает квадратурные правила Фелиппы для аппроксимации интегралов над внутренней частью треугольника в 2D.
TRIANGLE_INTEGRALS, библиотека C ++, которая возвращает точное значение интеграла любого одночлена над внутренней частью единичного треугольника в 2D.
TRIANGLE_LYNESS_RULE, библиотека C ++, которая возвращает квадратурные правила Лайнесса-Джесперсена над внутренней частью треугольника в 2D.
TRIANGLE_MONTE_CARLO, библиотека C ++, которая использует метод Монте-Карло для оценки интеграла функции над внутренней частью единичного треугольника в 2D.
TRIANGLE_NCC_RULE, библиотека C ++, которая определяет квадратурные правила Ньютона-Котеса (NCC) над внутренней частью треугольника в 2D.
TRIANGLE_NCO_RULE, библиотека C ++, которая определяет квадратурные правила Newton-Cotes Open (NCO) над внутренней частью треугольника в 2D.
TRIANGLE_WANDZURA_RULE, библиотека C ++, которая возвращает квадратурные правила точности 5, 10, 15, 20, 25 и 30 над внутренней частью треугольника в 2D.
WEDGE_FELIPPA_RULE, библиотека C ++, которая возвращает квадратурные правила для аппроксимации интегралов над внутренней частью клина агрегата в 3D.
Справка:
Хун Сяо, Жидрунас Гимбутас,
Численный алгоритм построения эффективной квадратуры правила в двух и более высоких измерениях,
«Компьютеры и математика с приложениями»,
Том 59, 2010 г., страницы 663-676.
Исходный код:
Примеры и тесты:
EQUI08 - это правило восьмой степени в равностороннем треугольнике.
SIMP08 - это симплексное правило степени 8.
USER08 - это правило степени 8 в указанном пользователем треугольнике в (1,0), (4,4), (0,3).
Список программ:
KJACOPOLS2 вычисляет многочлены Якоби и производные.
KJACOPOLS вычисляет многочлены Якоби.
KLEGEYPOLS3 вычисляет масштабированные полиномы Лежандра и производные.
KLEGEYPOLS вычисляет масштабированные полиномы Лежандра.
ORTHO2EVA0 вычисляет ортонормированные полиномы на треугольнике.
ORTHO2EVA30: ортонормированных многочленов и производных на треугольнике.
ORTHO2EVA3: значений ортогональных полиномов и производных, справочный треугольник.
ORTHO2EVA вычисляет ортогональные многочлены на контрольном треугольнике.
QUAECOPY2 копирует квадратурное правило в пользовательские массивы X, Y и W.
QUAECOPY копирует квадратурное правило в пользовательские массивы Z и W.
QUAEINSIDE проверяет, находится ли точка внутри треугольника.
QUAENODES2 расширяет узлы с 1/6 до 1/3 треугольника.
КВАЭНОДЫ расширяет узлы до ссылочного треугольника.
QUAEQUAD0 возвращает запрошенное квадратурное правило.
QUAEQUAD возвращает симметричную квадратурную формулу для ссылочного треугольника.
QUAEROTATE применяет ротацию.
R8VEC_COPY копирует R8VEC.
R8VEC_UNIFORM_01 возвращает единичный псевдослучайный R8VEC.
REF_TO_KOORN отображает точки из ссылки на треугольник Коорнвиндера.
REF_TO_TRIANGLE отображает точки из контрольного треугольника в треугольник.
RULE_COMPRESSED_SIZE возвращает сжатый размер запрошенного квадратурного правила.
RULE_FULL_SIZE возвращает полный размер запрошенного квадратурного правила.
RULE01 возвращает правило степени 1.
RULE02 возвращает правило степени 2.
RULE03 возвращает правило степени 3.
RULE04 возвращает правило степени 4.
RULE05 возвращает правило степени 5.
RULE06 возвращает правило степени 6.
RULE07 возвращает правило степени 7.
RULE08 возвращает правило степени 8.
RULE09 возвращает правило степени 9.
RULE10 возвращает правило степени 10.
RULE11 возвращает правило степени 11.
RULE12 возвращает правило степени 12.
ПРАВИЛО13 возвращает правило степени 13.
RULE14 возвращает правило степени 14.
RULE15 возвращает правило степени 15.
RULE16 возвращает правило степени 16.
RULE17 возвращает правило степени 17.
RULE18 возвращает правило степени 18.
ПРАВИЛО19 возвращает правило степени 19.
RULE20 возвращает правило степени 20.
ПРАВИЛО21 возвращает правило степени 21.
RULE22 возвращает правило степени 22.
ПРАВИЛО23 возвращает правило степени 23.
RULE24 возвращает правило степени 24.
RULE25 возвращает правило степени 25.
RULE26 возвращает правило степени 26.
ПРАВИЛО27 возвращает правило степени 29.
RULE28 возвращает правило степени 28.
ПРАВИЛО29 возвращает правило степени 29.
RULE30 возвращает правило степени 30.
ПРАВИЛО31 возвращает правило степени 31.
RULE32 возвращает правило степени 32.
RULE33 возвращает правило степени 33.
RULE34 возвращает правило степени 34.
RULE35 возвращает правило степени 35.
RULE36 возвращает правило степени 36.
RULE37 возвращает правило степени 37.
ПРАВИЛО38 возвращает правило степени 38.
RULE39 возвращает правило степени 39.
RULE40 возвращает правило степени 40.
RULE41 возвращает правило степени 41.
RULE42 возвращает правило степени 42.
ПРАВИЛО 43 возвращает правило степени 43.
RULE44 возвращает правило степени 44.
RULE45 возвращает правило степени 45.
ПРАВИЛО46 возвращает правило степени 46.
RULE47 возвращает правило 47 степени.
RULE48 возвращает правило 48 степени.
RULE49 возвращает правило степени 49.
RULE50 возвращает правило степени 50.
SIMPLEX_TO_TRIANGLE отображает точки симплекса в треугольник.
TIMESTAMP распечатывает текущую дату YMDHMS в качестве отметки времени.
TRIANGLE_AREA возвращает площадь треугольника.
TRIANGLE_TO_REF отображает точки из любого треугольника в контрольный треугольник.
TRIANGLE_TO_SIMPLEX отображает точки любого треугольника на симплекс.
TRIANMAP отображает правила из справочного треугольника в пользовательский треугольник.
TRIASIMP отображает точку опорного треугольника на симплекс.
TRIASYMQ возвращает симметричную квадратурную формулу для пользовательского треугольника.
TRIASYMQ_GNUPLOT: устанавливает график GNUPLOT для правила квадратуры треугольника.
Вы можете подняться на один уровень до исходные коды C ++.
Последний раз редактировалось 30 июня 2014 г.
научных статей, журналов, авторов, подписчиков, издателей
Как крупный международный издатель академических и исследовательских журналов Science Alert издает и разрабатывает названия в партнерстве с самыми престижные научные общества и издатели.Наша цель заключается в том, чтобы максимально широко использовать качественные исследования. аудитория.
Мы прилагаем все усилия, чтобы поддержать исследователей которые публикуют в наших журналах. Есть масса информации здесь, чтобы помочь вам публиковаться вместе с нами, а также ценные услуги для авторов, которые уже публиковались у нас.
2021 цены уже доступны. Ты может получить личную / институциональную подписку перечисленных журналы прямо из Science Alert. В качестве альтернативы вы возможно, пожелает связаться с выбранным вами агентством по подписке. Направляйте заказы, платежи и запросы в службу поддержки. в службу поддержки клиентов журнала Science Alert.
Science Alert гордится своей тесные и прозрачные отношения с обществом. В виде некоммерческий издатель, мы стремимся к самым широким возможное распространение публикуемых нами материалов и на предоставление услуг высочайшего качества нашим издательские партнеры.
Здесь вы найдете ответы на наиболее часто задаваемые вопросы (FAQ), которые мы получили по электронной почте или через контактную форму в Интернете.В зависимости от характера вопросов мы разделили часто задаваемые вопросы на разные категории.
Азиатский индекс научного цитирования (ASCI) стремится предоставить авторитетный, надежный и значимая информация по освещению наиболее важных и влиятельные журналы для удовлетворения потребностей мировых научное сообщество.
Разное
Навигация по записям
« Композитные трубы для отопления – преимущества и недостатки, сравнительный анализ, особенности установки в отопительных системах
Пол в бане своими руками – Пол в бане своими руками »
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Поиск
Search for:
Рубрики
Виды
Виды отопления
Заливка
Ленточный фундамент
Советы строителя
Столбчатый фундамент
Строение
Фундамент
Разное
© 2024 SeaSide-Home
Карта сайта

Площадь треугольника

Формула площади треугольника

Через основание и высоту:

По трём сторонам через полупериметр —

Похожие калькуляторы:

Формулы площади треугольника

Формулы площади треугольника

Через основание и высоту

Через две стороны и угол

Формула Герона

Через радиус вписанной окружности

Через радиус описанной окружности

Площадь прямоугольного треугольника

Площадь прямоугольного треугольника

Формула Герона для прямоугольного треугольника

Площадь равнобедренного треугольника

Площадь равнобедренного треугольника

Площадь равнобедренного треугольника

Формула Герона для равнобедренного треугольника

Площадь равностороннего треугольника

Площадь равностороннего треугольника

Площадь равностороннего треугольника

Площадь равностороннего треугольника

Расчет периметра и площади треугольника

Площадь треугольника через основание и высоту: a×h/2

Периметр треугольника: (a + b + c)

Площадь равностороннего треугольника: (√(3)/4)×a²

Площадь равнобедренного треугольника(2 стороны и угол): ½×a×b×SinC

Формулы площади треугольника:

Примеры :

Площадь треугольника

Формулы площади треугольника

Задача. Изменение площади при изменении длины сторон

Площадь равнобедренного треугольника — формула, пример расчета, калькулятор

Площадь треугольника – прямоугольного или равнобедренного, формула

Треугольник: определение и виды фигуры

Как вычислить площадь треугольника?

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Определение площади треугольника с неизвестными данными

Известны основание и высота

Известны величины трех сторон

Известны две стороны и угол между ними

Известны одна сторона и прилежащие к ней углы

Известны радиус вписанной окружности и полупериметр

Известны радиус описанной окружности и периметр

Площадь треугольника

Площадь треугольника формула

QUADRATURE_RULES_TRI — Квадратурные правила для треугольников

Пример:

Лицензирование:

Связанные данные и программы:

Рекомендации:

Образцы файлов:

Двумерный

Трехмерный

(PDF) Квадратура Гаусса Лежандра над треугольником

Симметричные квадратурные правила для треугольников.

Лицензирование:

Языки:

Связанные данные и программы:

Справка:

Исходный код:

Примеры и тесты:

Список программ:

научных статей, журналов, авторов, подписчиков, издателей

Добавить комментарий Отменить ответ