Калькулятор развертки конуса: Онлайн калькулятор: Развертка (выкройка) конуса

Развертка усеченного и прямого конуса

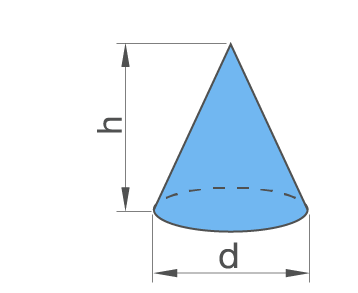
Расчёт развёртки конуса

Введите размеры в мм, и тип конуса:

Результат расчёта:

Скачать, сохранить результат

Выберите способ сохранения

Информация

Часто в строительной практике или даже повседневной жизни приходится сталкиваться с необходимостью построения конуса. Процесс построения требует определенных знаний и высокой точности, иначе конус будет иметь определенные отклонения от необходимых параметров и это может привести к тем или иным неприятным последствиям. Расчет развертки конуса является важнейшей частью при создании выкройки для конуса. Данный показатель относительный и при его расчете необходимо знать ряд других параметров. При этом, необходимо понимать, что существует два вида конусов. Первый вид называется «Прямой конус», то есть классическом его понимании. Второй вид называется «Усеченный конус» — часть конуса, которая заключается между основанием и секущей плоскостью, параллельной его основанию. Расчет развертки прямого конуса отличается от того, как производится расчет развертки усеченного конуса. Отличие заключается в том, что у усеченного конуса появляется еще одна переменная и по итогу расчета калькулятор сообщает в расчете не только расстояние и угол, но и два радиуса.

Наш онлайн калькулятор имеет встроенные формулы, что позволяет производить расчет данных показателей, просто выбрав вид конуса и введя абсолютные значения в соответствующие ячейки. Возможности и принцип построения системы калькулятора исключают допущение ошибок при расчетах, и избавляют пользователя от необходимости в самостоятельном детальном изучении методик расчета.

Преимущества, которые дает онлайн калькулятор

• Большая экономия времени;
• Гарантированно правильный и предельно точный расчет;
• Удобный интерфейс, который будет понятен даже новичку;
• Открытый доступ к калькулятору для всех пользователей.

Таким образом, можно сделать вывод, что расчет развертки конуса требует концентрации внимания на многих деталях, и самостоятельный его расчет является достаточно трудоемким. Наш онлайн калькулятор является инструментом, который упростит Вашу жизнь при точном расчете данного показателя. Также Вам доступна информация о том, какая формула применяется при расчете и определенная справочная информация.

поделиться и оценить

Смотрите также:

Добавить комментарий

Развертка конуса — онлайн калькулятор

Данный калькулятор может пригодится инженерам-технологам или инженерам-конструкторам, то есть всем тем, кому часто приходится рассчитывать развертку прямого конуса обычного и усеченного.

Сам калькулятор ниже, он может рассчитать все необходимые параметры развертки прямого кругового конуса.

Калькулятор рассчитывает параметры развертки прямого кругового конуса на плоскости — визуально это можно посмотреть на рисунке внизу.

The field is not filled.

‘%1’ is not a valid e-mail address.

Please fill in this field.

The field must contain at least% 1 characters.

The value must not be longer than% 1 characters.

Field value does not coincide with the field ‘%1’

An invalid character. Valid characters:’%1′.

Expected number.

It is expected a positive number.

Expected integer.

It is expected a positive integer.

The value should be in the range of [%1 .. %2]

The ‘% 1’ is already present in the set of valid characters.

The field must be less than 1%.

The first character must be a letter of the Latin alphabet.

Su

Mo

Tu

We

Th

Fr

Sa

January

February

March

April

May

June

July

August

September

October

November

December

century

B.C.

%1 century

An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3

Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

s.sh.

u.sh.

v.d.

z.d.

yes

no

Wrong file format. Only the following formats: %1

Please leave your phone number and / or email.

Калькуляторы расчета размеров развертки конуса

Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты  и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами

Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Шаг 1 – определение длины образующей L

(Если она уже известна – шаг пропускается)

Перейти к расчётам

Шаг 2 – определение радиусов внутренней и внешней дуги развертки

Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.

Шаг 3 – определение величины центрального угла f

Перейти к расчётам

*  *  *  *  *  *  *

Итак, все данные имеются. Остается на листе бумаги циркулем провести две дуги рассчитанных радиусов. А затем из точки центра с помощью транспортира прочертить два луча под рассчитанным углом – они ограничат развертку по угловой длине.

Существуют и чисто геометрические методы построения довольно точной развертки конуса, без проведения расчётов. Один из них подробно описан в статье нашего портала «Как сделать абажур своими руками».

Объем прямого/усеченного конуса — калькулятор онлайн + формулы

Скачать, сохранить результат

Выберите способ сохранения

Информация

Математика является основой всего, что нас окружает. Она особенно важна в таких сферах деятельности, как технологии, строительство и техника. Еще в средней школе дети начинают изучать различные математические законы, формулы и много другое. Одной из важнейших формул выступает формула, по которой находится объем конуса. Данная формула применяется специалистами во многих видах деятельности. Также часто применяется формула, по которой вычисляют объем усеченного конуса.

В профессиональной деятельности у инженера или строителя нет права на допущение ошибки. Это связанно с тем, что их ошибка может стоить кому-нибудь жизни. Для того, чтобы облегчить и обезопасить расчеты в профессиональной деятельности, был создан такой инструмент, как онлайн-калькулятор. Он позволяет совершать вычислительные действия любых показателей, вводя исходные значения в формулу. Калькулятор выдает предельно точный результат и исключает возможность возникновения ошибки в процессе вычислений.

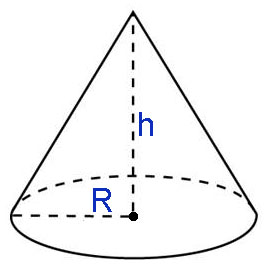
Для вычислений в данном калькуляторе используется три основные формулы:

1. Формула для вычисления объема конуса через радиус и высоту.
2. Формула отвечающая на вопрос « Как найти объем конуса через площадь его основания и высоту?».
3. Последняя формула позволяет найти объем усеченного конуса, зная радиус и высоту.

Используя наш онлайн-калькулятор, Вы получаете следующие выгоды:

• Точность и достоверность результатов проведенного вычисления, которая полностью исключает ошибки в процессе осуществления профессиональной деятельности.
• Экономия времени, благодаря исключению необходимости самостоятельных расчетов.
• Интерфейс нашего калькулятора разработан максимально простым и удобным.

Для того, чтобы использовать наш онлайн-калькулятор, необходимо совершить следующие действия:

• Выбрать вид конуса (прямой или усеченный).
• Ввести исходные данные (высота, радиус, площадь).
• Введя необходимы данные калькулятор автоматически сообщит, что объем конуса равен тому или иному значению.

поделиться и оценить

Смотрите также:

Добавить комментарий

Как сделать ровный конус из бумаги. Как сделать развертку – выкройку для конуса или усеченного конуса заданных размеров. Простой расчет развертки

Как сделать развертку – выкройку для конуса или усеченного конуса заданных размеров. Простой расчет развертки.

Иногда возникает задача – изготовить защитный зонт для вытяжной или печной трубы, вытяжной дефлектор для вентиляции и т.п. Но прежде чем приступить к изготовлению, надо сделать выкройку (или развертку) для материала. В интернете есть всякие программы для расчета таких разверток. Однако задача настолько просто решается, что вы быстрее рассчитаете ее с помощью калькулятора (в компьютере), чем будете искать, скачивать и разбираться с этими программами.

Начнем с простого варианта — развертка простого конуса. Проще всего объяснить принцип расчета выкройки на примере.

Допустим, нам надо изготовить конус диаметром D см и высотой H сантиметров. Совершенно понятно, что в качестве заготовки будет выступать круг с вырезанным сегментом. Известны два параметра – диаметр и высота. По теореме Пифагора рассчитаем диаметр круга заготовки (не путайте с радиусом готового конуса). Половина диаметра (радиус) и высота образуют прямоугольный треугольник. Поэтому:

Итак, теперь мы знаем радиус заготовки и можем вырезать круг.

Вычислим угол сектора, который надо вырезать из круга. Рассуждаем следующим образом: Диаметр заготовки равен 2R, значит, длина окружности равна Пи*2*R — т.е. 6.28*R. Обозначим ее L. Окружность полная, т.е. 360 градусов. А длина окружности готового конуса равна Пи*D. Обозначим ее Lm. Она, естественно, меньше чем длина окружности заготовки. Нам нужно вырезать сегмент с длиной дуги равной разности этих длин. Применим правило соотношения. Если 360 градусов дают нам полную окружность заготовки, то искомый угол должен дать длину окружности готового конуса.

Из формулы соотношения получаем размер угла X. А вырезаемый сектор находим путем вычитания 360 – Х.

Из круглой заготовки с радиусом R надо вырезать сектор с углом (360-Х). Не забудьте оставить небольшую полоску материала для нахлеста (если крепление конуса будет внахлест). После соединения сторон вырезанного сектора получим конус заданного размера.

Например: Нам нужен конус для зонта вытяжной трубы высотой (Н) 100 мм и диаметром (D) 250 мм. По формуле Пифагора получаем радиус заготовки – 160 мм. А длина окружности заготовки соответственно 160 x 6,28 = 1005 мм. В тоже время длина окружности нужного нам конуса — 250 x 3,14 = 785 мм.

Тогда получаем, что соотношение углов будет такое: 785 / 1005 x 360 = 281 градус. Соответственно вырезать надо сектор 360 – 281 = 79 градусов.

Расчет заготовки выкройки для усеченного конуса.

Такая деталь бывает нужна при изготовлении переходников с одного диаметра на другой или для дефлекторов Вольперта-Григоровича или Ханженкова. Их применяют для улучшения тяги в печной трубе или трубе вентиляции.

Задача немного осложняется тем, что нам неизвестна высота всего конуса, а только его усеченной части. Вообще же исходных цифр тут три: высота усеченного конуса Н, диаметр нижнего отверстия (основания) D, и диаметр верхнего отверстия Dm (в месте сечения полного конуса). Но мы прибегнем к тем же простым математическим построениям на основе теоремы Пифагора и подобия.

В самом деле, очевидно, что величина (D-Dm)/2 (половина разности диаметров) будет относиться с высотой усеченного конуса Н так же, как и радиус основания к высоте всего конуса, как если бы он не был усечен. Находим полную высоту (P) из этого соотношения.

Отсюда Р = D x H / (D-Dm).

Теперь зная общую высоту конуса, мы можем свести решение задачи к предыдущей. Рассчитать развертку заготовки как бы для полного конуса, а затем «вычесть» из нее развертку его верхней, ненужной нам части. А можем рассчитать непосредственно радиусы заготовки.

Получим по теореме Пифагора больший радиус заготовки — Rz. Это квадратный корень из суммы квадратов высоты P и D/2.

Меньший радиус Rm – это квадратный корень из суммы квадратов (P-H) и Dm/2.

Теперь осталось рассчитать угол сектора, который надо вырезать.

Длина окружности нашей заготовки равна 2 х Пи х Rz, или 6,28 х Rz. А длина окружности основания конуса – Пи х D, или 3,14 х D. Соотношение их длин и дадут соотношение углов секторов, если принять, что полный угол в заготовке – 360 градусов.

Т.е. Х / 360 = 3,14 x D / 6.28 x Rz

Отсюда Х = 180 x D / Rz (Это угол, который надо оставить, что бы получить длину окружности основания). А вырезать надо соответственно 360 – Х.

Например: Нам надо изготовить усеченный конус высотой 250 мм, диаметр основание 300 мм, диаметр верхнего отверстия 200 мм.

Находим высоту полного конуса Р: 300 х 250 / (300 – 200) = 600 мм

По т. Пифагора находим внешний радиус заготовки Rz: Корень квадратный из (300/2)^2 + 6002 = 618,5 мм

По той же теореме находим меньший радиус Rm: Корень квадратный из (600 – 250)^2 + (200/2)^2 = 364 мм.

Определяем угол сектора нашей заготовки: 180 х 300 / 618,5 = 87.3 градуса.

На материале чертим дугу с радиусом 618,5 мм, затем из того же центра – дугу радиусом 364 мм. Угол дуги может имеет примерно 90-100 градусов раскрытия. Проводим радиусы с углом раскрытия 87.3 градуса. Наша заготовка готова. Не забудьте дать припуск на стыковку краев, если они соединяются внахлест.

Константин Тимошенко © 31.07.2014 г.

Как вы решили этот пример? 300 х 250 / (300 – 200) = 600 мм

Калькуляторы расчета размеров развертки конуса

Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Шаг 1 – определение длины образующей L

(Если она уже известна – шаг пропускается)

Шаг 2 – определение радиусов внутренней и внешней дуги развертки

Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.

Построение развертки конуса

Развертка поверхности конуса — это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.

Варианты построения развертки:

Развертка прямого кругового конуса

Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.

В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.

1. Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
2. Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.

На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.

Рассмотрим треугольник S_{AB. Длины его сторон SA и SB равны образующей l конической поверхности. Величина AB соответствует длине A’B’. Для построения треугольника SAB в произвольном месте чертежа откладываем отрезок SA=l, после чего из точек S и A проводим окружности радиусом SB=l и AB= A’B’ соответственно. Соединяем точку пересечения окружностей B с точками A и S.}

Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
   Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’₁ занимает положение, при котором она параллельна фронтальной плоскости π₂. Соответственно, S’’5’’₁ – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S_{16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’1, 16=1’6’.}

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
3. Находим положение точек A_{, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.}
4. Соединяем точки A_{, B, C плавной линией.}

Развертка усеченного конуса

Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.

Источники:

http://samodel.pro/raznoe/raznoe19.html
http://stroyday.ru/kalkulyatory/obshhestroitelnye-voprosy/kalkulyatory-rascheta-razmerov-razvertki-konusa.html
http://ngeometry.ru/postroenie-razvertki-konusa.html

Выкройка для конуса | Математика для ювелиров

19.11.2012 // Владимир Трунов   

Вместо слова «выкройка» иногда употребляют «развертка», однако этот термин неоднозначен: например, разверткой называют инструмент для увеличения диаметра отверстия, и в электронной технике существует понятие развертки. Поэтому, хоть я и обязан употребить слова «развертка конуса», чтобы поисковики и по ним находили эту статью, но пользоваться буду словом «выкройка».

Построение выкройки для конуса — дело нехитрое. Рассмотрим два случая: для полного конуса и для усеченного. На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).

---

1. Полный конус

Обозначения:

• — диаметр основания конуса;
• — высота конуса;
• — радиус дуги выкройки;
• — центральный угол выкройки.

Параметры выкройки рассчитываются по формулам:
;
;
где .

---

2. Усеченный конус

Обозначения:

Формулы для вычисления параметров выкройки:
;
;
;
где .
Заметим, что эти формулы подойдут и для полного конуса, если мы подставим в них .

---

3. Угол при вершине конуса

Иногда при построении конуса принципиальным является значение угла при его вершине (или при мнимой вершине, если конус усеченный). Самый простой пример — когда нужно, чтобы один конус плотно входил в другой. Обозначим этот угол буквой (см. картинку).
В этом случае мы можем его использовать вместо одного из трех входных значений: , или . Почему «вместо«, а не «вместе«? Потому что для построения конуса достаточно трех параметров, а значение четвертого вычисляется через значения трех остальных. Почему именно трех, а не двух и не четырех — вопрос, выходящий за рамки этой статьи. Таинственный голос мне подсказывает, что это как-то связано с трехмерностью объекта «конус». (Сравните с двумя исходными параметрами двухмерного объекта «сегмент круга», по которым мы вычисляли все остальные его параметры в статье Геометрия круга.)

Ниже приведены формулы, по которым определяется четвертый параметр конуса, когда заданы три.

---

4. Методы построения выкройки

• Вычислить значения на калькуляторе и построить выкройку на бумаге (или сразу на металле) при помощи циркуля, линейки и транспортира.
• Занести формулы и исходные данные в электронную таблицу (например, Microsoft Exel). Полученный результат использовать для построения выкройки при помощи графического редактора (например, CorelDRAW).
• использовать мою программу Cones, которая нарисует на экране и выведет на печать выкройку для конуса с заданными параметрами. Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.

---

5. Не параллельные основания

Что касается усеченных конусов, то программа Cones пока строит выкройки для конусов, имеющих только параллельные основания.
Для тех, кто ищет способ построения выкройки усеченного конуса с не параллельными основаниями, привожу ссылку, предоставленную одним из посетителей сайта:
Усеченный конус с не параллельными основаниями.

прямой, наклонный и усеченный конус

Развертка поверхности конуса — это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.

Варианты построения развертки:

Развертка прямого кругового конуса

Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.

В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.

Алгоритм построения

1. Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
2. Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.

Пример

На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.

Рассмотрим треугольник S₀A₀B₀. Длины его сторон S₀A₀ и S₀B₀ равны образующей l конической поверхности. Величина A₀B₀ соответствует длине A’B’. Для построения треугольника S₀A₀B₀ в произвольном месте чертежа откладываем отрезок S₀A₀=l, после чего из точек S₀ и A₀ проводим окружности радиусом S₀B₀=l и A₀B₀= A’B’ соответственно. Соединяем точку пересечения окружностей B₀ с точками A₀ и S₀.

Грани S₀B₀C₀, S₀C₀D₀, S₀D₀E₀, S₀E₀F₀, S₀F₀A₀ пирамиды SABCDEF строим аналогично треугольнику S₀A₀B₀.

Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

Алгоритм

1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
   Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’₁ занимает положение, при котором она параллельна фронтальной плоскости π₂. Соответственно, S’’5’’₁ – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S₀1₀6₀, S₀6₀5₀, S₀5₀4₀, S₀4₀3₀, S₀3₀2₀, S₀2₀1₀. Построение каждого треугольника выполняется по трем сторонам. Например, у △S₀1₀6₀ длина S₀1₀=S’’1’’₀, S₀6₀=S’’6’’₁, 1₀6₀=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

Алгоритм

1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
3. Находим положение точек A₀, B₀, C₀ на соответствующих им ребрах пирамиды, откладывая на развертке отрезки S₀A₀=S’’A’’, S₀B₀=S’’B’’₁, S₀C₀=S’’C’’₁.
4. Соединяем точки A₀, B₀, C₀ плавной линией.

Развертка усеченного конуса

Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.

Алгоритм

1. Строим вспомогательный конус ε, подобный конусу ω, как это показано на рисунке выше. Для удобства построения величину диаметра d выбираем таким образом, чтобы соотношение t=D/d выражалось целым числом. В рассматриваемом примере t=2.
2. Строим развертку боковой поверхности конуса ε – S₀A₀1₀2₀3₀4₀5₀A₀ и на биссектрисе угла A₀S₀A₀ отмечаем точку O₀, выбрав ее расположение произвольно.
3. Проводим прямые O₀A₀, O₀1₀, O₀2₀, O₀3₀, O₀4₀, O₀5₀, O₀A₀ и на них откладываем отрезки [O₀A₁₀]=t×|O₀A₀|, [O₀1₁₀]= t×|O₀1₀|, [O₀2₁₀]=t×|O₀2₀|, [O₀3₁₀]=t×|O₀3₀|, [O₀4₁₀]=t×|O₀4₀|, [O₀5₁₀]=t×|O₀5₀|, [O₀A₁₀]=t×|O₀A₀| соответственно, где t=D/d. Соединяем точки A₁₀, 1₁₀, 2₁₀, 3₁₀, 4₁₀, 5₁₀, A₁₀ плавной линией.
4. Из точек A₁₀, 1₁₀, 2₁₀, 3₁₀, 4₁₀, 5₁₀, A₁₀ проводим лучи, которые параллельны соответственно прямым A₀S₀, 1₀S₀, 2₀S₀, 3₀S₀, 4₀S₀, 5₀S₀, A₀S₀, и на них откладываем отрезки A₁₀B₁₀, 1₁₀1₂₀, 2₁₀2₂₀, 3₁₀3₂₀, 4₁₀4₂₀, 5₁₀5₂₀, A₁₀B₁₀, равные l – образующей усеченного конуса. Проводим линию B₁₀1₂₀2₂₀3₂₀4₂₀5₂₀B₁₀.

Калькулятор конуса

, вы вводите любые три из следующих значений: диаметр малого конца, диаметр большого конца, длина канавки и конус / лапка, а мы предоставляем четвертый.

Калькулятор конуса: вы вводите любые три из следующих значений: диаметр малого конца, диаметр большого конца, длина канавки и конус / лапка, а мы предоставляем четвертый.

Вы вводите любые три малых диаметра конца, Большой диаметр конца, длина канавки и конус / лапка, и мы предоставляем четвертый.

Заполните 3 из 4 полей, перечисленных ниже, чтобы получить 4-е.

(Введите размеры 1, 2 и 3 в десятичных дюймах. Пример 1/4 «= 0,250)

спасибо Gammons за этот калькулятор

Вернуться к началу страницы

ссылка на продукт оглавление ссылка на «НОВОЕ» ссылка на прайс-лист

Newman Tools Inc.
185 Iber Road
Stittsville, Ottawa, Ontario, Canada K2S 1E7
Телефон: 1-613-836-6776 или 1-800-465-1384
Факс: 1-613-836 — 9070 или 1-800-605-2442

Newman Tools Inc.
151 New Park Avenue
Hartford, CT 06106, USA
Телефон: 1-800-465-1384
Факс: 1-800-605-2442

Электронная почта: [email protected]

---

Комментарии, вопросы, электронная почта присылайте по адресу [email protected] ( это электронное письмо будет возвращено с предложением повторно отправить электронное письмо на следующий адрес электронной почты)

spamfilter1 «в» newmantools «точка» com. Это обозначение предназначено для того, чтобы роботы не смогли получить это электронное письмо. адрес.

вернуться к Ньюману Домашняя страница инструментов.

---

Перейти … На главную Страница | марка Индекс имени | Товар список | технический информация | Цена список | ежемесячно специальные предложения $$$$ | Шутки | Последний добавления страниц | контакт Информация | Эл. адрес Boss

---

Обслуживание Канадские провинции Ньюфаундленд, Новая Шотландия, Нью-Брансуик, Остров Принца Эдуарда, Квебек, Онтарио, Манитоба, Саскачеван, Альберта, Британская Колумбия и штаты Алабама, Аляска, Аризона, Арканзас, Калифорния, Колорадо, Коннектикут, Делавэр, Флорида, Джорджия, Гавайи, Айдахо, Иллинойс, Индиана, Айова, Канзас, Кентукки, Луизиана, Мэн, Мэриленд, Массачусетс, Мичиган, Миннесота, Миссисипи, Миссури, Монтана, Небраска, Невада, Нью-Гэмпшир, Нью-Джерси, Нью-Мексико, Нью-Йорк, Северная Каролина, Северная Дакота, Огайо, Оклахома, Орегон, Пенсильвания, Род-Айленд, Южная Каролина, Южная Дакота, Теннесси, Техас, Юта, Вермонт, Вирджиния, Вашингтон, Западная Вирджиния, Висконсин, Вайоминг

---

обновлено в ноябре 2008 г.
Newman Tools Inc.
марта 2007 г.
Newman Tools Inc. ,

Калькулятор сна

• 8
• 9
• 10
• 11
• 12
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8

• 00
• 05
• 10
• 15
• 20
• 25
• 30
• 35
• 40
• 45
• 50
• 55
• 00
• 05
• 10
• 15
• 20
• 25
• 30
• 35
• 40
• 45
• 50
• 55
• 00

Если я сейчас пойду спать…

Среднему человеку требуется около 15 минут, чтобы заснуть.
Если вы ложитесь спать прямо сейчас, вам следует попытаться проснуться в один из следующих моментов:

• 22:45
• 00:15
• 1:45
• 3:15
• 4:45
• 6:15

Если вы проснетесь в один из этих периодов, вы проснетесь между 90-минутными циклами сна.Хороший ночной сон состоит из 5-6 полных циклов сна.
Попробуйте свет для пробуждения с имитацией восхода солнца, который обеспечивает приятное и естественное начало утра.

Рассчитать заново

Среднему человеку требуется около 15 минут, чтобы заснуть.
Чтобы проснуться отдохнувшим, вам следует лечь спать в один из следующих периодов:

• 22:45
• 00:15
• 1:45
• 3:15
• 4:45
• 6:15

Если вы проснетесь в один из этих периодов, вы проснетесь между 90-минутными циклами сна.Хороший ночной сон состоит из 5-6 полных циклов сна.
Попробуйте свет для пробуждения с имитацией восхода солнца, который обеспечивает приятное и естественное начало утра.

Рассчитать заново

,Калькулятор

: Кузнечное дело — The RuneScape Wiki

Из RuneScape Wiki, вики для всего, что связано с RuneScape

Для этого динамического калькулятора требуется JavaScript.

• При использовании ковки рекомендуется убедиться, что Result Sorting , Item Forged и Metal не установлены на «Все», так как список элементов очень обширен
• Для всех Сортировка результатов методов, кроме «Все», результаты ограничиваются 50 лучшими методами.
• Значения для автонагревателя и нулевой тепловой обработки немного искажены. Когда преимущество выравнивания для запуска при максимальном нагреве разблокировано, каждый новый созданный элемент позволит вам AFK на 33% (66% с формой перегрева) при сильном нагреве, а затем множитель среднего нагрева, прежде чем перейти к низкому нагреву. Калькулятор не учитывает это, вместо этого он всегда предполагает низкий множитель тепла (или средний множитель тепла с активной формой перегрева). Таким образом, если прогресс элемента достаточно низкий (т.е. бронза) вы всегда будете на сильном огне. Я попытаюсь исправить это, но пока предположим, что ставки немного выше (тем меньше, чем меньше предметов вы делаете в час; эффект должен быть незначительным для старшей руны, но весьма заметен для бронзы, однако низкий прогресс бронзы означает переключение на сильный нагрев даст более точную цифру).
• Hellion aura принимает плоские 10% и не учитывает импульсное ядро ​​(из-за того, что оно имеет собственное поле).
• Калькулятор учитывает обязательную потерю тиков (т.е. тики, что у есть , должны быть потрачены не из-за человеческой ошибки. Например, два тика потрачены на ковку предмета, тики потрачены впустую при повторном нагреве и т. Д.).
• Superheat item позволяет разогревать без потерь.
• «Свободных» слитков, выплавленных за час, означает, сколько дополнительных бесплатных слитков получено от «Двойного шанса плавки».

• 2-Ticking : заклинание Superheat Item после каждого удара с использованием перка Кузнечного мастерства. Калькулятор включает элемент перегрева, если выбран этот метод.
• High Heat : поддержание незавершенного нагрева повторно, чтобы температура никогда не опускалась ниже 66%. Форма перегрева позволяет игрокам упасть до 33%.
• AFK с автонагревателем : AFK с автонагревателем, использующим уголь. 100-300 угля в час.
• Обработка без нагрева : AFK без использования автонагревателя.

Добавить [

.

Калькулятор кроссовера — Хорошие калькуляторы

Этот калькулятор кроссовера может использоваться для расчета пассивных фильтров (первого, второго, третьего и четвертого порядка) в двух- и трехканальных сетях кроссовера. Он также создаст принципиальную схему и предоставит требуемые значения компонентов.

Инструкции: Выберите тип кроссовера (двухполосный или трехполосный), значения входного импеданса для твитера, вуфера и среднего диапазона (с трехполосным кроссовером), выберите порядок / тип фильтра, введите кроссовер частота и нажмите кнопку «Рассчитать».После этого калькулятор предоставит значения компонентов, необходимые для выбранного вами типа кроссовера.

В калькуляторе кроссовера используются следующие формулы:

Формулы проектирования сети с двусторонним кроссовером

	Баттерворта 1-го порядка	Solen Split 1-го порядка -6 дБ
C1 =	.159 / R H f	.1125 / (R H f)
L1 =	R L /6.28f	.2251R L / f

	2-й порядок Бессель	2-й порядок Баттерворт	2-й порядок Чебышев	2-й порядок Линквиц-Райли
C1 =	.0912 / (R H f)	.1125 / (R H f)	.1592 / (R H f)	.0796 / (R H е)
C2 =	.0912 / (R L f)	.1125 / (R L f)	. 1592 / (R L f)	. 0796 / (R L f)
L1 =	.2756R H / f	.2251R H / f	.1592R H / f	.3183R H / f
L2 =	.2756R L / f	.2251R L / f	.1592R L / f	.3183R L / f

	Баттерворта 3-го порядка	3-го порядка Бесселя
C1 =	.1061 / (R H f)	0,0791 / (R H f)
C2 =	. 3183 / (R H f)	.3953 / (R H f)
C3 =	. 2122 / (R L f)	. 1897 / (R L f)
L1 =	.1194R H / f	.1317R H / f
L2 =	.2387R L / f	.3294R L / f
L3 =	.0796R L / F	. 0659R L / F

	4-й порядок Бесселя	4-й порядок Баттерворта	4-й порядок Гауссиан
C1 =	.0702 / (R H f)	.1040 / (R H f)	.0767 / (R H f)
C2 =	. 0719 / (R H f)	. 1470 / (R H f)	.1491 / (R H f)
C3 =	. 2336 / (R L f)	. 2509 / (R L f)	. 2235 / (R L f)
C4 =	.0504 / (R L f)	.0609 / (R L f)	.0768 / (R L f)
L1 =	.0862R H / f	.1009R H / f	.1116R H / f
L2 =	.4983R H / f	.4159R H / f	.3251R H / f
L3 =	.3583R L / f	.2437R L / f	.3253R L / f
L4 =	.1463R L / f	.1723R L / f	.1674R L / f

	4-й порядок Legendre	4-й порядок Линейно-фазовый	4-й порядок Linkwitz-Riley
C1 =	.1104 / (R H f)	. 0741 / (R H f)	.0844 / (R H f)
C2 =	.1246 / (R H f)	.1524 / (R H f)	.1688 / (R H f)
C3 =	. 2365 / (R L f)	.2255 / (R L f)	. 2533 / (R L f)
C4 =	.0910 / (R L f)	.0632 / (R L f)	.0563 / (R L f)
L1 =	.1073R H / f	.1079R H / f	.1000R H / f
L2 =	.2783R H / f	.3853R H / f	.4501R H / f
L3 =	.2294R L / f	.3285R L / f	.3000R L / f
L4 =	.2034R L / f	. 1578R L / f	.1500R L / f

Примечание. Значения указаны в фарадах (C1 — Cn), Генри (L1 — Ln), герцах (f) и омах (R _H , R _L ).

Формулы проектирования трехполосной кроссоверной сети

	Нормальная полярность 1-го порядка f H / f L = 10	Нормальная полярность 1-го порядка f H / f L = 8
C1 =	.1590 / (R H f H )	. 1590 / (R H f H )
C2 =	.5540 / (R M f M )	. 5070 / (R M f M )
L1 =	.0458R M / f M	.0500R M / f M
L2 =	.1592R L / f L	.1592R L / f L

	2-й порядок (обратная полярность средних частот) f H / f L = 10	2-й порядок (обратная полярность средних частот) f H / f L = 8
C1 =	.0791 / (R H f H )	. 0788 / (R H f H )
C2 =	. 3236 / (R M f M )	. 3046 / (R M f M )
C3 =	.0227 / (R M f M )	.0248 / (R M f M )
C4 =	.0791 / (R L f L )	.0788 / (R L f L )
L1 =	.3202R H / f H	.3217R H / f H
L2 =	1.0291R M / f M	.9320R M / f M
L3 =	.0837R M / f M	.0913R M / f M
L4 =	. 3202R L / f L	.3217R L / f L
	Коэффициент усиления полосы пропускания = 2.08db	Bandpass Gain = 2,45 дБ

	Нормальная полярность 3-го порядка f H / f L = 10	Нормальная полярность 3-го порядка f H / f L = 8
C1 =	. 1138 / (R H f H )	.1158 / (R H f H )
C2 =	,2976 / (R H f H )	.2927 / (R H f H )
C3 =	. 0765 / (R M f M )	.0884 / (R M f M )
C4 =	. 3475 / (R M f M )	. 3112 / (R M f M )
C5 =	1.068 / (R M f M )	.9667 / (R M f M )
C6 =	.2127 / (R L f L )	. 2130 / (R L f L )
L1 =	.1191R H / f H	.1189R H / f H
L2 =	.0598R M / f M	.0634R M / f M
L3 =	.0253R M / f M	.0284R M / f M
L4 =	.3789R M / f M	.3395R M / f M
L5 =	.2227R L / f L	.2187R L / f L
L6 =	.0852R L / f L	.0866R L / f L
	Коэффициент усиления полосы пропускания = 0,85 дБ	Коэффициент усиления полосы пропускания = 0,99 дБ

	3-й порядок (обратная полярность средних частот) f H / f L = 10	3-й порядок (обратная полярность средних частот) f H / f L = 8
C1 =	.0995 / (R H f H )	0,0980 / (R H f H )
C2 =	.3402 / (R H f H )	.3459 / (R H f H )
C3 =	.0683 / (R M f M )	.0768 / (R M f M )
C4 =	. 3128 / (R M f M )	. 2793 / (R M f M )
C5 =	1.148 / (R M f M )	1.061 / (R M f M )
C6 =	. 2126 / (R L f L )	. 2129 / (R L f L )
L1 =	.1191R H / f H	.1190R H / f H
L2 =	.0665R M / f M	.0711R M / f M
L3 =	.0233R M / f M	.0254R M / f M
L4 =	.4285R M / f M	.3951R M / f M
L5 =	. 2546R L / f L	.2586R L / f L
L6 =	.0745R L / f L	.0732R L / f L
	Коэффициент усиления полосы пропускания = 1.6 дБ	Коэффициент усиления полосы пропускания = 2,1 дБ

	Нормальная полярность 4-го порядка f H / f L = 10	Нормальная полярность 4-го порядка f H / f L = 8
C1 =	. 0848 / (R H f H )	.0849 / (R H f H

.