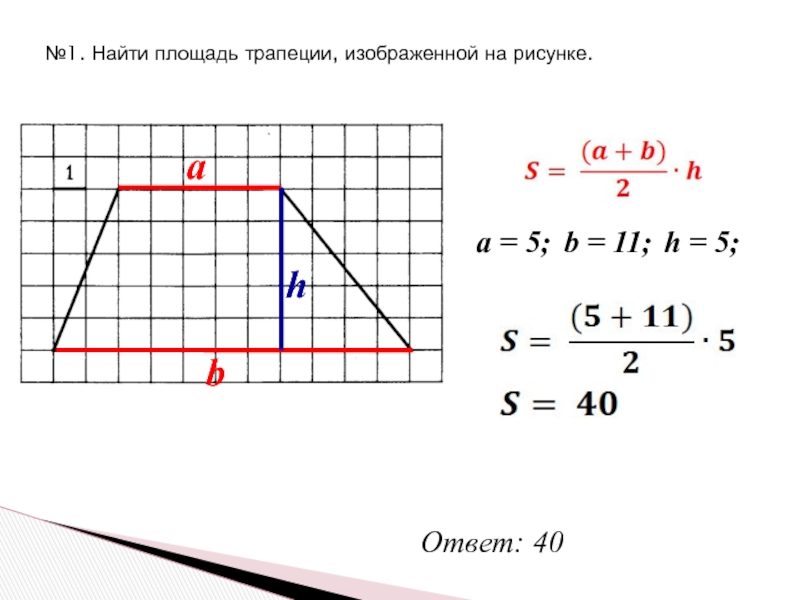
В центре Петербурга пройдет праздник «К Островскому на площадь Островского»
4 июня площадь перед Александринским театром и близлежащие к ней территории вдоль Екатерининского сквера превратятся в пространство творчества. Здесь состоится праздник «К Островскому на площадь Островского», посвященный 100-летию площади и 200-летию великого писателя.В этом году Площадь Островского празднует свой юбилей. 100 лет назад, 6 октября 1923 года, место перед Александринским театром получило новое название – площадь Островского. Изначально она была Аничковская. 13 августа 1832 года она стала Александринской. Именно столетию современного названия площади, а также 200-летию со дня рождения А.Н. Островского и будет посвящено действо.
В 12:00 начнется интерактивная театральная программа. Каждый сможет почувствовать себя героем пьес драматурга. На тротуарах расположатся театральные зоны, где все желающие смогут войти в образ, подобрав себе грим и костюм.
Одна зона будет посвящена трилогии о Мишеньке Бальзаминове, другая – пьесе «На всякого мудреца довольно простоты».Помимо участия в актерской импровизации, гости праздника смогут попробовать себя и в других театральных профессиях, например, в режиссуре или в художественном оформлении сцены. Интерактивная театральная программа пройдет с 12:00 до 17:00.
Параллельно с работой театральных зон начнется экскурсионная программа. Гиды расскажут об истории здания Александринского театра и самой площади, о личности Островского и его значении для петербургского театра. Спектакли по пьесам драматурга есть практически в каждом театре, и это неслучайно. Его произведения всегда актуальны, острохарактерны и дают актерам прекрасную возможность раскрыть свой творческий диапазон.
С 13:00 до 15:00 на Большой сцене праздника пройдет концерт «Необыкновенный Островский» с участием петербургских театров, имеющих в своем репертуаре постановки по пьесам драматурга.
Мероприятие проводит Некоммерческое партнерство содействия реализации культурных проектов «Искусство XXI век», Музыкальный театр им. Ф.И. Шаляпина и Театр-фестиваль «Балтийский дом» при поддержке Комитета по культуре Санкт-Петербурга.
Вход свободный.
Наш Telegram
в Петербурге пройдет театрализованный музыкальный праздник
Фото: Александр Глуз/ «Петербургский дневник»Четвертого июня в Петербурге пройдет общегородской театрализованный музыкальный праздник.
Его посвятят главному юбиляру года драматургу Александру Островскому, 200-летний юбилей которого отмечается в этому году, и 100-летию площади, названной в его честь.
«Будет масштабно, ярко, необычно!» – заверили устроители праздника. И пообещали, что его участники смогут почувствовать себя героями пьес Островского, отточить свое мастерство в Академии ремесел, совершить экскурсию в Александринку, увидеть спектакли ведущих театров и послушать музыку, навеянную пьесами драматурга.
Непростой выбор
Праздник, идею которого предложил председатель Комитета по культуре Федор Болтин, пройдет в Петербурге впервые. Но даже среди множества других мероприятий он едва ли затеряется – столько всего интересного и необычного ждет гостей в этот день.
Начнется торжество сразу после выстрела из пушки Петропавловской крепости. И тут придется делать выбор. Можно, например, заглянуть в Академию ремесел, появление которой на площади не случайно. Дело в том, что Островский страстно увлекался резьбой по дереву.
И в своем имении в Щелыково даже организовал столярную мастерскую.
На площади под руководством опытных мастеров можно будет освоить азы традиционных русских промыслов и собственными руками изготовить сувенир на память. А можно, если есть задатки актера, преобразиться в героев пьес Островского. Помогут в этом профессиональные костюмеры и гримеры.
Ну а те, кому мало школьных знаний о русском Шекспире, смогут совершить бесплатную экскурсию в Александринский театр. Специалисты расскажут о его истории и судьбе постановок по пьесам Островского. А ставили их здесь 244 раза!
Виртуальный памятник
Одним из главных событий праздника станет представление «Необыкновенный Островский». Впервые на одной сцене соберутся ведущие театры города, чтобы показать свои новые постановки.
Одно перечисление участников заставит биться сильнее сердце любого театрала. Молодежный театр на Фонтанке, Театр имени Ленсовета, Театр комедии имени Н. П. Акимова, драматический театр «На Литейном», театр «Русская антреприза» имени Андрея Миронова, Театр эстрады имени Аркадия Райкина, Драматический театр на Васильевском и один из организаторов праздника – театр-фестиваль «Балтийский дом».
Артисты покажут фрагменты из своих лучших спектаклей и создадут нерукотворный памятник драматургу.
«В Москве есть памятник Островскому, но нет площади его имени. А в Петербурге есть площадь, но нет памятника», – пошутил директор «Балтийского дома» Сергей Шуб. На празднике это положение исправят. Каждый театр, выходящий на сцену, внесет свой вклад в «строительство». И зрители увидят, как виртуальный памятник драматургу постепенно приобретает законченный вид.
Кульминация дня
В 17.00 пространство площади зальет музыка. На сцену выйдет оркестр Музыкального театра имени Ф. И. Шаляпина (театр «Мюзик-Холл») «Северная симфония» под управлением маэстро Фабио Мастранджело.
«Мы хотим подчеркнуть необыкновенную музыкальность Островского. Показать, как он представлен в музыке», – объяснила директор театра Юлия Стрижак.
Вместе с режиссером концерта Виктором Высоцким она пообещала, что творчество знаменитого драматурга предстанет в совершенно новом ракурсе, так как к известным монологам присоединится пение, балет и музыка.
Не все, к примеру, знают, что к сочинениям Островского не раз обращались великие композиторы. Именно с его пьес начинал свой путь Петр Чайковский (опера «Воевода»), а драма «Гроза» вдохновила чешского классика Леоша Яначека на оперу «Катя Кабанова». Более того, знаменитую «Снегурочку» Островского прославили в музыке сразу два гения – Петр Ильич и Римский-Корсаков.
Музыкальный спектакль станет кульминационной точкой праздника. На него прибудет сам драматург в исполнении Николая Смирнова. Вместе со своим коллегой Максимом Ханжовым они поговорят о жизни Островского и приоткроют секреты его творчества.
«Для Петербурга наследие Островского крайне важно. Свидетельство тому – план общегородских мероприятий, подписанный губернатором Александром Дмитриевичем Бегловым. В него вошло порядка 140 событий, которые состоятся в течение всего юбилейного года», – подытожил Федор Болтин.
Справка
Изначально площадь в центре Невского проспекта была обозначена как Аничковская.
«Зенит» пропустил от «Сочи» уже на 34-й секунде, но отыгрался и довел матч до ничьей
Завершение квадрата
» Завершение Квадрата » вот где мы…
| … возьмем квадратное уравнение следующим образом: | и превратите его в это: | |
| топор 2 + Ьх + с = 0 | а(х+ d ) 2 + е = 0 |
Для тех из вас, кто торопится, могу сказать, что: d = b 2a
и: e = c − b 2 4a
Но если у вас есть время, позвольте мне показать вам, как « Заполнить Квадрат » самостоятельно.
Завершение квадрата
Скажем, у нас есть простое выражение вида x 2 + bx. Наличие x дважды в одном и том же выражении может усложнить жизнь. Что мы можем сделать?
Что ж, немного вдохновившись геометрией, мы можем преобразовать его вот так:
Как видите x 2 + bx можно переставить почти в квадрат…
… и мы можем завершить квадрат с помощью (b/2) 2
В алгебре это выглядит так:
| x 2 + шт | + (б/2) 2 | = | |
| «Заполните квадрат » |
Итак, сложив (b/2) 2 , мы можем завершить квадрат.
Результат (x+b/2) 2 имеет x только один раз , что проще в использовании.
Сохранение равновесия
Теперь… мы не можем просто добавить (b/2) 2 без вычесть тоже! В противном случае меняется все значение.
Итак, давайте посмотрим, как это сделать правильно на примере:
| Начните с: | |
| (в данном случае «b» равно 6) | |
| Заполните квадрат: | |
| Также вычесть новый срок |
Упростите это, и все готово. | |
Результат:
x 2 + 6x + 7 = (x+3) 2 − 2
И теперь x появляется только один раз, и наша работа выполнена!
Быстрый подход
Вот быстрый способ получить ответ.
Вам может понравиться этот метод.
Сначала подумайте о желаемом результате: (x+d) 2 + e
После расширения (x+d) 2 получаем: x 2 + 2dx + d 2 + e
Теперь посмотрим, сможем ли мы преобразовать наш пример в эту форму, чтобы обнаружить d и e
Пример: попробуйте уместить x
2 + 6x + 7 в x 2 + 2dx + d 2 + eТеперь мы можем «форсировать» ответ:
- Мы знаем, что 6x должно закончиться как 2dx, поэтому d должно быть 3
- Далее мы видим, что 7 должно стать d 2 + e = 9 + e, поэтому e должно быть −2
И мы получаем тот же результат (x+3) 2 − 2, что и выше!
Теперь давайте рассмотрим полезное приложение: решение квадратных уравнений…
Решение общих квадратных уравнений путем заполнения квадрата
Мы можем дополнить квадрат до решить квадратное уравнение (найти где оно равно нулю).
Но общее квадратное уравнение может иметь коэффициент а перед х 2 :
топор 2 + Ьх + с = 0
Но с этим легко справиться… просто сначала разделите все уравнение на «а», а затем продолжайте:
х 2 + (б/а)х + с/а = 0
шагов
Теперь мы можем решить квадратное уравнение за 5 шагов:
- Шаг 1 Разделите все члены на a (коэффициент x 2 ).
- Шаг 2 Переместите числовое выражение ( c/a ) в правую часть уравнения.
- Шаг 3 Заполните квадрат в левой части уравнения и сбалансируйте его, добавив такое же значение в правую часть уравнения.
Теперь у нас есть что-то похожее на (x + p) 2 = q, которое можно довольно легко решить:
- Шаг 4 Извлеките квадратный корень из обеих частей уравнения.
- Шаг 5 Вычтите число, оставшееся в левой части уравнения, чтобы найти x .
Примеры
Хорошо, несколько примеров помогут!
Пример 1: решить x
2 + 4x + 1 = 0Шаг 1 можно пропустить в этом примере, так как коэффициент x 2 равен 1
Шаг 2 Переместите числовой член в правую часть уравнения: 900 05
x 2 + 4x = -1
Шаг 3 Заполните квадрат в левой части уравнения и уравновесьте его, добавив то же число в правую часть уравнения.
(б/2) 2 = (4/2) 2 = 2 2 = 4
x 2 + 4x + 4 = -1 + 4
(x + 2) 2 = 3
Шаг 4 Извлеките квадратный корень из обеих частей уравнения:
х + 2 = ±√3 = ±1,73 (до 2 знаков после запятой)
Шаг 5 Вычтите 2 с обеих сторон:
x = ±1,73 – 2 = -3,73 или -0,27
А вот еще интересная и полезная штука. В конце шага 3 у нас было уравнение: (х + 2) 2 = 3 Это дает нам вершину (точка поворота) x 2 + 4x + 1: (-2, -3) |
Пример 2: решить 5x
2 – 4x – 2 = 0Шаг 1 Разделить все члены на 5
Шаг 2 Переместите числовой член в правую часть уравнения:
x 2 – 0,8x = 0,4
Шаг 3 Заполните квадрат в левой части уравнения и уравновесьте его, добавив то же самое число в правой части уравнения:
(b/2) 2 = (0,8/2) 2 = 0,4 2 = 0,16
x 2 – 0,8x + 0,16 = 0,4 + 0,16
(x – 0,4) 2 = 0,56
Шаг 4 Извлеките квадратный корень из обеих частей уравнения:
x – 0,4 = ±√0,56 = ±0,748 (до 3 знаков после запятой)
Шаг 5 Вычтите (-0,4) с обеих сторон (другими словами, прибавьте 0,4):
x = ±0,748 + 0,4 = — 0,348 или 1,148
Почему «Завершить квадрат»?
Зачем заполнять квадрат, если мы можем просто использовать квадратную формулу, чтобы решить квадратное уравнение?
Ну, одна причина указана выше, где новая форма не только показывает нам вершину, но и упрощает решение.
Бывают также случаи, когда форма ax 2 + bx + c может быть частью более крупного вопроса , и перестановка его в виде a(x+ d ) 2 + e упрощает решение, потому что x появляется только один раз.
Например, «x» может быть функцией (например, cos(z) ), и ее изменение может открыть путь к лучшему решению.
Также завершение квадрата является первым шагом в выводе квадратичной формулы
Думайте об этом как о еще одном инструменте в вашем наборе математических инструментов.
364, 1205, 365, 2331, 2332, 3213, 3896, 3211, 3212, 1206
Сноска: значения «d» и «e»
Как я получил значения d и e из верхней части страницы?
| Начните с | |
| Разделить уравнение на a | |
| Положить c/a на другую сторону | |
| Добавить (b/2a) 2 на обе стороны | |
| «Заполни квадрат» | |
Теперь верни все обратно. .. | |
| … на левую сторону | |
| … к исходному множителю a x 2 | |
И вы заметите, что у нас есть:
a(x+d) 2 + e = 0
Где:d = б 2а
и: е = с — б 2 4a
Как вверху страницы!
Квадратное число — Элементарная математика
Неформально: когда вы умножаете целое число («целое» число, положительное, отрицательное или ноль) на себя, полученное произведение называется квадратным числом, или совершенным квадратом, или просто «квадратом». ” Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — все числа квадратные.
Более формально: квадратное число — это число вида n × n или n 2 , где n — любое целое число.
Объекты, расположенные в виде квадратного массива
Название «квадратное число» происходит от того факта, что эти определенные количества объектов могут быть расположены так, чтобы заполнить идеальный квадрат.
Дети могут поэкспериментировать с монетками (или квадратными плитками), чтобы увидеть, какое их число можно расположить в идеально квадратном ряду.
Четыре пенни могут:
Девять пенни могут:
И шестнадцать пенни тоже могут:
Но семь пенни или двенадцать пенни не могут быть расположены таким образом. Числа (объектов), которые можно расположить в виде квадратного массива, называются «квадратными числами».
Квадратные массивы должны быть заполнены, если мы хотим подсчитать число как квадратное число. Здесь 12 копеек расположены в виде квадрата, но не полного квадратного массива, поэтому 12 не является квадратным числом.
Число 12 не квадратное.
Детям может понравиться изучение того, сколько копеек можно разложить на таком открытом квадрате. Их не называют «квадратными числами», но они следуют интересному шаблону.
Квадраты из квадратных плиток тоже интересно делать. Число квадратных плиток, которые вписываются в квадратный массив, является «квадратным числом».
Вот две доски, 3×3 и 5×5 . Сколько красных плиток в каждой? Черный? Желтый?
Есть ли какие-либо из этих квадратных чисел?
Что, если таким же образом замостить доску 4 × 4 или 6 × 6 ?
Можете ли вы предсказать количество плиток на доске 7 × 7 или 10 × 10 ?
Квадратные числа в таблице умножения
Квадратные числа расположены по диагонали стандартной таблицы умножения.
Соединения с треугольными числами
Если вы посчитаете зеленые треугольники в каждом из этих рисунков, вы увидите последовательность чисел: треугольные числа.
Если посчитать белые треугольники, находящиеся в «пробелах» между зелеными, последовательность чисел начинается с 0 (поскольку в первом дизайне нет пробелов) и продолжается: 1, 3, 6, 10, 15, …, опять треугольные числа!
Удивительно, но если вы посчитаете все крошечные треугольники в каждом дизайне — и зеленые, и белые — цифры будут квадратными!
Связь между квадратными и треугольными числами, увиденная с другой стороны
Постройте ступенчатое расположение стержней Кюизенера, скажем, W, R, G. Затем постройте следующую ступеньку: W, R, G, P.
Каждый является «треугольным» (если не учитывать ступенчатое ребро). Сложите два последовательных треугольника вместе, и они образуют квадрат: . Этот квадрат такого же размера, как 16 белых палочек, расположенных в квадрате. Число 16 — это квадратное число, «4 в квадрате», квадрат длины самого длинного стержня (измеренного белыми стержнями).
Вот еще пример: . Если их сложить вместе, они образуют квадрат, площадь которого равна 64, что опять-таки является квадратом длины (в белых стержнях) самого длинного стержня.
(Коричневый стержень имеет длину 8 белых стержней, а 64 — это 8, умноженное на 8, или «8 в квадрате».)
Лестничные ступени из квадратных чисел
Лестничные ступени, которые поднимаются, а затем снова опускаются, как здесь, также содержат квадратное число плиток. Когда плитки расположены в шахматном порядке, как здесь, дополнительное предложение, описывающее количество красных плиток (10), количество черных плиток (6) и общее количество плиток (16), снова показывает связь между треугольные числа и квадратные числа: 10 + 6 = 16.
Предлагая детям 2-го (или даже 1-го) класса построить узоры в виде ступенек и написать числовые предложения, описывающие эти узоры, — хороший способ дать им возможность попрактиковаться с описательными числовыми предложениями. а также подружиться с квадратными числами.
Вот два примера. Цвет используется здесь, чтобы помочь вам увидеть то, что описывается. Детям нравится цвет, но он им не нужен, и они часто видят творческие способы описания узоров ступеней, которые они построили из одноцветных плиток.