Объем емкости онлайн калькулятор: Расчет объема емкости в литрах

Онлайн-калькулятор расчета объема цилиндра: через диаметр, радиус

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В публикации представлены онлайн-калькуляторы и формулы для расчета объема цилиндра через площадь основания/радиус/диаметр и высоту.

• Расчет объема
  • Через площадь основания и высоту
  • Через радиус основания и высоту
  • Через диаметр основания и высоту

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислен объем фигуры с учетом указанных данных.

Через площадь основания и высоту

Формула расчета

Через радиус основания и высоту

Формула расчета

Через диаметр основания и высоту

Формула расчета

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

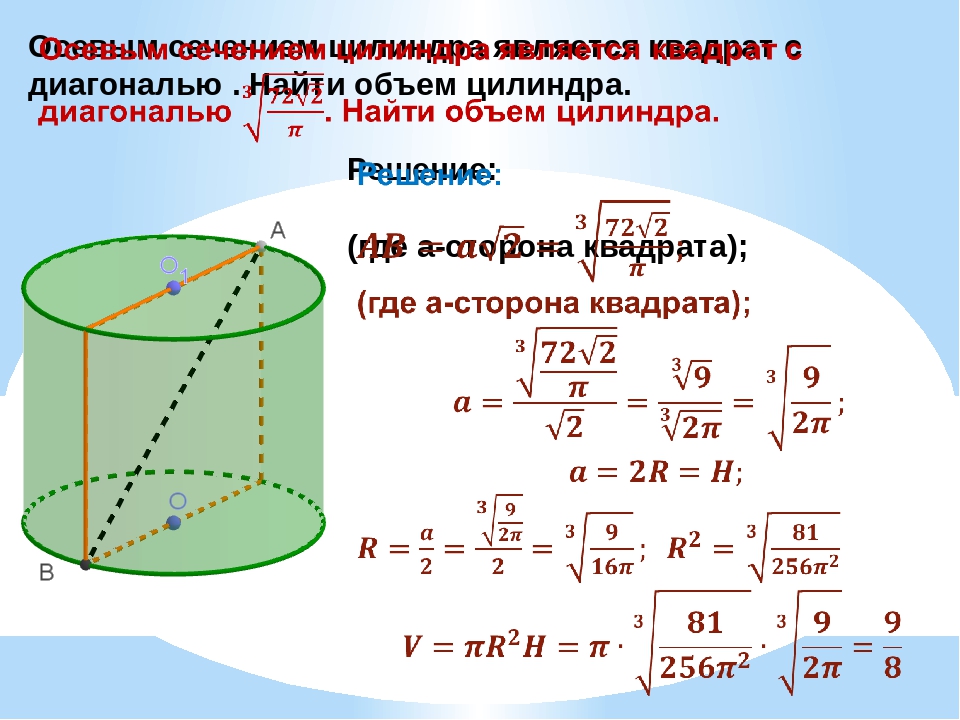
Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Объём стенки цилиндра — онлайн калькулятор

1. Главная
2. /
3. Математика
4. /
5. Геометрия
6. /
7. Объём стенки цилиндра

Чтобы посчитать объём стенки цилиндра, то есть объём полого цилиндра, воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Найти чему равен объём полого цилиндра (V_ст) можно зная (либо-либо):

• Высоту цилиндра h, внешний радиус r₁ и внутренний радиус r₂
• Высоту цилиндра h, внешний диаметр d₁ и внутренний диаметр d₂
• Высоту цилиндра h, внешний радиус r₁ и толщину стенки δ
• Высоту цилиндра h, внутренний радиус r₂ и толщину стенки δ
• Высоту цилиндра h, внешний диаметр d₁ и толщину стенки δ
• Высоту цилиндра h, внутренний диаметр d₂ и толщину стенки δ

Зная оба радиуса (диаметра)

Чему равен объём стенки цилиндра V_ст если:

Внешний радиус r1диаметр d1 =
Внутренний радиус r2диаметр d2 =
Высота цилиндра h =
Ответ: V

ст =

Зная толщину стенки

Чему равен объём стенки цилиндра V_ст если:

Внешний радиус r1 Внутренний радиус r2 Внешний диаметр d1 Внутренний диаметр d2 =
Толщина стенки δ =
Высота цилиндра h =
Ответ: V_ст =

Теория

Чему равен объём полого цилиндра V_ст если:

Формулы

Через радиусы или диаметры цилиндра

V_ст = π ⋅ (r₁² — r₂²) ⋅ h , где r₁ — внешний радиус, r₂ — внутренний радиус , а h — высота

V_ст = π ⋅ ((^d₁/₂)² — (^d₂/₂)²) ⋅ h , где d₁ — внешний диаметр, d₂ — внутренний диаметр, а h — высота

Через толщину стенки цилиндра

V_ст = π ⋅ (d₂ ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, d₂ — внутренний диаметр, а h — высота

V_ст = π ⋅ ((d₁ — 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, d₁ — внешний диаметр, а h — высота

V_ст = π ⋅ (2 ⋅ r₂ ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, r₂ — внутренний радиус, а h — высота

V_ст = π ⋅ ((2 ⋅ r₁ — 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, r₁ — внешний радиус, а h — высота

Пример №1

К примеру, посчитаем каков объём металла в трубе, если её длинна 3 метра, внешний диаметр d₁=5 см, а внутренний d₂=4. 5 см?

V_ст = 3.14 ⋅ ((⁵/₂)² — (^4.5/₂)²) ⋅ 300 = 3.14 ⋅ (6.25 — 5.0625) ⋅ 300 ≈ 1119 см³

Пример №2

Теперь посчитаем объём металла в этой же 3-х метровой трубе, но возьмём внутренний радиус r₂ = 2.25 см и толщину стенки δ = 0.25 см (при этом у нас должен получится тот же ответ, что и в предыдущем примере):

V_ст = 3.14 ⋅ (2 ⋅ 2.25 ⋅ 0.25 + 0.25²) ⋅ 300 = 3.14 ⋅ 1.1875 ⋅ 300 ≈ 1119 см³

См. также

Расчет объема

Расчет объема

ДЕП Дом	Вода/сточные воды Математический калькулятор Танк Калькулятор объема Возврат в информационный центр оператора
Формула: Д х Ш x D = кубических футов *** Кубический футов x 7,47 = галлонов	Объем квадратного или прямоугольного резервуара или отстойника Пожалуйста введите данные о длине, ширине и глубине боковой воды. Бак Д Длина (футы) введите длину Бак Ш ширина (футы) введите ширину Боковой Вода D Высота (фут) введите глубину Нажмите на кнопку для расчета кубических футов Нажмите на кнопку для расчета галлонов
Формула: 3. 1417 x R x D = кубические футы **** Кубический футов х 7,47 = Галлоны	Объем круглого бака или очистителя Пожалуйста введите данные для радиуса резервуара (радиус составляет 1/2 диаметра) и стороны глубина воды. Бак R радиус (фут): введите радиус (1/2 диаметра) Бак Боковая вода D epth (ft): введите глубину Нажмите на кнопку, чтобы рассчитать куб. футов Нажмите на кнопка для расчета объема воды (галлоны)

 

Container Loading Calculator — расчет вместимости контейнера (штабелирование, стафировка). Контейнерный калькулятор.

Используйте этот калькулятор, чтобы легко рассчитать, сколько предметов определенных размеров можно поместить в контейнер. Калькулятор штабелирования контейнеров.

    Быстрая навигация:

1. Использование калькулятора контейнеров
2. Список стандартных типов контейнеров
3. Загрузка контейнера: расчет внутреннего штабелирования
4. Использование контейнера и простота внутреннего штабелирования

    Использование калькулятора контейнеров

Это довольно простой калькулятор загрузки контейнеров: он позволяет вам рассчитать, сколько предметов одинаковых размеров и веса (опционально) можно поместить в один транспортный контейнер . В настоящее время он поддерживает только простую укладку, что означает, что каждый элемент будет размещен рядом с другим, без сложных поворотов или упорядочения. В то время как сложное упорядочение может в некоторых случаях привести к укладке немного большего количества предметов, людям, заполняющим контейнеры, также сложнее точно следовать.

Для вашего удобства мы ввели 8 наиболее часто используемых размеров контейнеров в международных перевозках, чтобы вы могли быстрее произвести расчеты. Для каждого из них у нас также есть оценка максимальной загрузки, поэтому, если вы введете вес предмета, мы также рассчитаем общий вес груза и предупредим вас, если он превысит максимальную грузоподъемность контейнера. Ниже приведен список стандартных размеров и максимального веса груза.

    Список стандартных типов контейнеров

В таблице представлены размеры 8 стандартных типов контейнеров, предварительно определенных в нашем калькуляторе. Внутренние размеры немного отличаются от минимального внутреннего размера в стандарте ISO 668:2013, поскольку на практике большинство производителей поставляют контейнеры с большими внутренними размерами (большая вместимость, больший внутренний объем), чем минимальные спецификации. Максимальная полезная нагрузка рассчитывается на основе стандарта ISO за вычетом общего веса тары.

Так как каждый производитель выпускает немного разные контейнеры, если вы знаете точные размеры и максимальную грузоподъемность, то лучше указать их с помощью опции «Индивидуальный» нашего калькулятора контейнеров.

Размеры стандартных контейнеров

Тип контейнера	Внутренние размеры (Ширина x Длина x Высота)	Макс. вес груза
45 футов, стандарт	2 340 x 13 550 x 2 360 мм = 2,34 x 13,55 x 2,36 м (7,677 x 44,455 x 7,74 фута)	28 000 кг (61 729 фунтов)
Высокий куб 45 футов	2 340 x 13 550 x 2 655 мм = 2,34 x 13,55 x 2,655 м = (7,677 x 44,455 x 8,71 фута)	27 800 кг (61 288 фунтов)
40 футов, стандарт	2 350 x 12 030 x 2 390 мм = 2,35 x 12,03 x 2,39 м = (7,71 x 39,47 x 7,84 фута)	28 800 кг (63,493 фунта)
Высокий куб 40 футов	2 350 x 12 030 x 2 655 мм = 2,35 x 12,03 x 2,655 м = (7,71 x 44,455 x 8,71 фута)	28 600 кг (63 052 фунта)
30 футов, стандарт	2340 x 8940 x 2360 мм = 2,34 x 8,94 x 2,36 м = (7,677 x 29,33 x 7,74 фута)	28 400 кг (62 611 фунтов)
Высокий куб 30 футов	2 340 х 8 940 х 2 655 мм = 2,34 х 8,94 х 2,655 м = (7,677 х 29,33 х 8,71 фута)	28 200 кг (62 170 фунтов)
20-футовый стандартный	2350 x 5900 x 2390 мм = 2,35 x 5,9 x 2,39 м = (7,71 x 19,357 x 7,84 фута)	28 200 кг (62 170 фунтов)
Высокий куб 20 футов	2350 x 5900 x 2655 мм = 2,35 x 5,9 x 2,655 м = (7,71 x 19,357 x 8,71 фута)	28 000 кг (61 729 фунтов)

    Загрузка контейнера: расчет внутреннего штабелирования

Чтобы оценить, сколько предметов вы можете разместить, вам необходимо определить оптимальный способ их штабелирования, чтобы свести к минимуму неиспользуемый объем в контейнере. Это трудная для решения проблема, так называемая NP-сложная задача (NP-проблема означает «недетерминированные полиномиально приемлемые проблемы»), что означает, что их нельзя решить за полиномиальное время.

Однако, если мы ограничимся простым упорядочиванием предметов, в котором все предметы ориентированы одинаково по отношению к внутренней части контейнера , тогда есть только шесть способов расположить набор предметов с 3 измерениями ( груз ) в трехмерном ящике ( контейнер ) . Вы можете использовать наш Калькулятор комбинаций, чтобы проверить, что если вы не уверены — 3 объекта, выберите по 2 из каждого. Если мы обозначим ширину, высоту и длину каждого предмета с помощью w, h и l, а соответствующие размеры контейнера с помощью W, H и L, то они будут выглядеть так:0009

• Ориентация w вдоль W, h вдоль L, l вдоль H
• Ориентация w вдоль W, l вдоль L, h вдоль H
• Ориентация h вдоль W, w вдоль L, l вдоль H
• Ориентация h вдоль W, l вдоль L, w вдоль H
• Ориентация l вдоль W, w вдоль L, h вдоль H
• Ориентация l вдоль W, h вдоль L, w вдоль H

Как только вы узнаете выравнивание, вы можете рассчитать для каждого из шести порядков укладки, сколько предметов вы можете поместить в объем, итеративно добавляя элементы в каждом измерении контейнера, пока не закончится место в этом направлении. Затем вы можете сравнить общий используемый объем (или количество элементов, если элементы одинаковы) в каждом из шести случаев и выбрать вариант, который наилучшим образом использует доступное пространство. Или вместо того, чтобы выполнять всю эту тяжелую работу, вы можете позволить нашим 9Контейнерный калькулятор 0025 сделает всю работу за вас.

    Использование контейнеров в сравнении с простотой внутренней укладки изобретение Малкольма Маклина. Заметив, что значительная часть времени и затрат на перевозку грузов связана с портовыми расходами (некоторые анализы конца XIX в.50-е говорят, что 60-70%, другие находят более низкие цифры ~ 40% от общих затрат), Маклин изобрел транспортный контейнер, чтобы сократить время и стоимость доставки. Следует отметить, что затраты были не только прямые, но и убытки из-за повреждения груза при обработке, погрузке и выгрузке. Первые контейнеры компании McLean отправились в путь 26 апреля 1956 года. С тех пор стоимость погрузки упала с 5,86 до 0,16 доллара за тонну (снижение на 97 %)! Время погрузки сократилось с 1,3 тонны в час в 19от 65 до 30 тонн в час в 1970 году и до более чем 74 тонн в час к 1980 году. В середине 1980-х годов некоторые азиатские порты загружали 24 контейнера в час ^[3] ! (каждый из которых может быть загружен в разной степени, но возможно 28 тонн в контейнере)

До этого у вас были ящики, коробки, мешки, ящики, связки, бочки, канистры, бочки, ящики, катушки и т. д. Вам приходилось тратить огромное количество времени на ручную обработку всех этих мелких предметов разного размера и веса. Теперь, когда у вас есть контейнер, вам больше не нужно это делать, но если вы хотите максимально использовать его, это может означать увеличение объема ручной работы и ее сложности (и, следовательно, времени выполнения). В то время как для операторов портов и судов все зависит от того, сколько тонн они могут переместить в час, для людей, занимающихся перевозкой содержимого контейнеров, простота внутреннего штабелирования может иметь существенное значение, поэтому проконсультируйтесь с ними, если вы рассматриваете более сложную схему, которая будет использовать немного более высокий процент объема.