Правила как найти площадь: Как найти площадь фигуры, формула

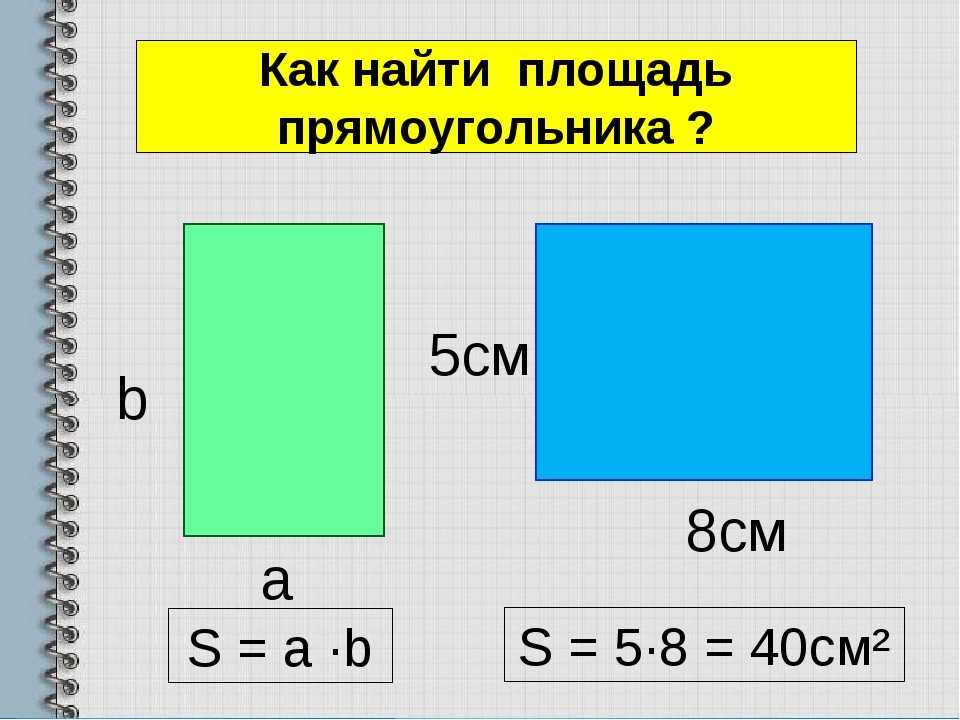
формула по длине стороны, диагонали

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади квадрата: формула и примеры

Квадрат – это геометрическая фигура; правильный четырехугольник, т.е. четырехугольник, имеющий равные стороны и углы (90°).

• Формула вычисления площади
• Примеры задач

Формула вычисления площади

1. По длине стороны: 

Площадь квадрата (S) равняется квадрату длины его стороны:

S = a²

Данная формула следует из того, что квадрат является частным случаем прямоугольника, площадь которого находится путем умножения его смежных сторон:

S = a*b

А т.к. все стороны квадрата равны, то вместо стороны b мы снова подставляем в формулу сторону a, т. е. S = a*a = a².

2. По по длине диагонали

Площадь квадрата равняется половине квадрата длины его диагонали:

S = d²/2

Соотношение стороны и диагонали квадрата: d=a√2.

Примеры задач

Задание 1
Найдите площадь квадрата, сторона которого равна 7 см.

Решение:
Используем формулу по длине стороны, т.е. S = 7² = 49 см².

Задание 2
Найдите площадь квадрата, диагональ которого равняется 4 см.

Решение 1:
Воспользуемся второй формулой (по длине диагонали): S = 4²/2 = 8 см².

Решение 2:
Мы можем выразить длину стороны через диагональ: a = 4/√2. И тогда, используя первую формулу, S = (4/√2)² = 8 см².

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Формулы площади.

Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса. Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Онлайн калькуляторы для вычисления площадей плоских фигур

Формулы площади треугольника

1. Формула площади треугольника по стороне и высоте
   Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

   S =	1	a · h
   	2

2. Формула площади треугольника по трем сторонам

   Формула Герона

   S = √p(p — a)(p — b)(p — c)

3. Формула площади треугольника по двум сторонам и углу между ними
   Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

   S =	1	a · b · sin γ
   	2

   S =	1	a · c · sin β
   	2

   S =	1	b · c · sin α
   	2

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности

   S =	a · b · с
   	4R

5. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
   Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

   S = p · r

   где S — площадь треугольника,
   a, b, c — длины сторон треугольника,
   h — высота треугольника,
   γ — угол между сторонами a и b,
   r — радиус вписанной окружности,
   R — радиус описанной окружности,
   

   p =	a + b + c	— полупериметр треугольника.
   	2

Вы можете воспользоваться онлайн калькулятором для расчета площади треугольника.

Формулы площади квадрата

1. Формула площади квадрата по длине стороны
   Площадь квадрата равна квадрату длины его стороны.

   S = a²

2. Формула площади квадрата по длине диагонали
   Площадь квадрата равна половине квадрата длины его диагонали.

   S =	1	d2
   	2

   где S — площадь квадрата,
   a — длина стороны квадрата,
   d — длина диагонали квадрата.

Вы можете воспользоваться онлайн калькулятором для расчета площади квадрата.

Формулы площади параллелограмма

1. Формула площади параллелограмма по длине стороны и высоте
   Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

   S = a · h

2. Формула площади параллелограмма по двум сторонам и углу между ними
   Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

   S = a · b · sin α

3. Формула площади параллелограмма по двум диагоналям и углу между ними
   Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

   S =	1	d1d2 sin γ
   	2

   где S — Площадь параллелограмма,
   a, b — длины сторон параллелограмма,
   h — длина высоты параллелограмма,
   d₁, d₂ — длины диагоналей параллелограмма,
   
   α — угол между сторонами параллелограмма,
   γ — угол между диагоналями параллелограмма.

Вы можете воспользоваться онлайн калькулятором для расчета площади параллелограмма.

Формулы площади ромба

1. Формула площади ромба по длине стороны и высоте
   Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

   S = a · h

2. Формула площади ромба по длине стороны и углу
   Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

   S = a² · sin α

3. Формула площади ромба по длинам его диагоналей
   Площадь ромба равна половине произведению длин его диагоналей.

   S =	1	d1 · d2
   	2

   где S — Площадь ромба,
   a — длина стороны ромба,
   h — длина высоты ромба,
   α — угол между сторонами ромба,
   d₁, d₂ — длины диагоналей.

Вы можете воспользоваться онлайн калькулятором для расчета площади ромба.

Формулы площади трапеции

1. Формула Герона для трапеции

   S =	a + b	√(p-a)(p-b)(p-a-c)(p-a-d)
   	|a — b|

2. Формула площади трапеции по длине основ и высоте
   Площадь трапеции равна произведению полусуммы ее оснований на высоту

   S =	1	(a + b) · h
   	2

   где S — площадь трапеции,
   a, b — длины основ трапеции,
   c, d — длины боковых сторон трапеции,
   

   p =	a + b + c + d	— полупериметр трапеции.
   	2

Вы можете воспользоваться онлайн калькулятором для расчета площади трапеции.

Формулы площади выпуклого четырехугольника

1. Формула площади четырехугольника по длине диагоналей и углу между ними

   Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

   S =	1	d 1 d2 sin α
   	2

   где S — площадь четырехугольника,
   d₁, d₂ — длины диагоналей четырехугольника,
   α — угол между диагоналями четырехугольника.

2. Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)

   Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

   S = p · r

3. Формула площади четырехугольника по длине сторон и значению противоположных углов

   S = √(p — a)(p — b)(p — c)(p — d) — abcd cos²θ

   где S — площадь четырехугольника,

   a, b, c, d — длины сторон четырехугольника,

   p = a + b + c + d2 — полупериметр четырехугольника,

   θ = α + β2 — полусумма двух противоположных углов четырехугольника.

   
   

4. Формула площади четырехугольника, вокруг которого можно описать окружность

   S = √(p — a)(p — b)(p — c)(p — d)

Вы можете воспользоваться онлайн калькулятором для расчета площади четырехугольника.

Формулы площади круга

1. Формула площади круга через радиус
   Площадь круга равна произведению квадрата радиуса на число пи.

   S = π r²

2. Формула площади круга через диаметр
   Площадь круга равна четверти произведения квадрата диаметра на число пи.

   S =	1	π d2
   	4

   где S — Площадь круга,
   r — длина радиуса круга,
   d — длина диаметра круга.

Вы можете воспользоваться онлайн калькулятором для расчета площади круга.

Все таблицы и формулы

Как найти площадь прямоугольника?

Площадь прямоугольника — один из самых важных и популярных параметров прямоугольника. В этой статье мы рассмотрим основные теории и математические формулы, связанные с площадью прямоугольника, например, площадь прямоугольника, формулу площади прямоугольника и ее применение в повседневной жизни.

Все ли мы знаем, что такое прямоугольник? Во-первых, давайте разберемся с некоторыми фундаментальными понятиями, связанными с прямоугольником. Прямоугольник — это замкнутая фигура, состоящая из 4 сторон, как и квадрат. Но, в отличие от квадрата, у прямоугольника не все стороны равны. Прямоугольник – это четырехсторонняя фигура, у которой противоположные стороны равны и параллельны. Чтобы понять это, посмотрите на рисунок ниже:

Вы можете видеть, что сторона, отмеченная как A, противоположна стороне, отмеченной как C, и равна стороне, отмеченной как C. Точно так же сторона, отмеченная как B, равна и противоположна стороне, отмеченной как D. Следовательно, ABCD — прямоугольник.

«Вы также можете заметить, что квадрат — это частный случай прямоугольников, у которых все противоположные стороны равны».

В повседневной жизни мы можем встретить прямоугольники повсюду. Блокноты, на которых вы пишете книги, которые вы изучаете, представляют собой прямоугольники. Некоторыми прекрасными примерами прямоугольных форм являются плитка, установленная в вашем доме, школьная доска, которую учитель использует в школе, обеденный стол, форма вашего телевизионного экрана и многое другое.

Давайте теперь изучим некоторые математические термины и понятия, связанные с прямоугольником:

• У прямоугольника только противоположные стороны равны и параллельны. Две смежные стороны никогда не бывают равными в случае прямоугольника.
• Прямоугольник — это параллелограмм. Это означает, что противоположные стороны прямоугольника равны и параллельны друг другу, или противоположные стороны никогда не пересекаются.
• Диагональ прямоугольника делит его на два равновеликих треугольника.
• Периметр прямоугольника: Расстояние, пройденное границей прямоугольника, называется периметром прямоугольника. Это математически формулируется как

P (прямоугольник) = 2 (длина + ширина)

Теперь, когда мы хорошо разобрались с основами прямоугольника, давайте узнаем площадь прямоугольника и формулу площади прямоугольника.

Какова площадь прямоугольника?

Все ли мы знакомы с определением «площади», прежде чем углубляться в площадь прямоугольника? Пространство, заметаемое или покрываемое любой замкнутой фигурой, называется площадью. Площадь фигуры – это площадь, которая лежит внутри границ этой фигуры. Это приводит нас к выводу, что площадь прямоугольника относится к области, которую он заметает или покрывает. Другими словами, площадь прямоугольника — это двумерная область, расположенная внутри его периметра.

Ниже приведен рисунок. Площадь прямоугольника обозначена закрашенной желтой областью, а его граница обозначена красной линией.

Далее в этой статье мы увидим формулу площади прямоугольника. Используя эту формулу, вы даже можете определить площадь пола вашего дома, площадь экрана вашего компьютера или мобильного телефона и т. д.

Как найти площадь прямоугольника?

Количество единичных квадратов, которые идеально помещаются внутри прямоугольника, дает площадь этого прямоугольника. Вы могли запутаться с этим определением, не так ли? Не волнуйся; давайте проясним это для вас.

Например, давайте сделаем прямоугольник с длиной = 2 см и шириной = 3 см. Попробуем теперь поместить внутри этого прямоугольника квадраты длины 1 единица.

«Единичная длина: 1 известна как единичная длина. Единицами измерения могут быть см, дюймы, м, футы и т. д., но помните, что всякий раз, когда пишется единица измерения длины, всегда понимайте ее как 1».

Таким образом, квадраты единичной длины означают, что длина каждой стороны квадрата равна единице. Как мы видим на рисунке ниже, 6 квадратов единичной длины могут легко поместиться внутри этого прямоугольника, поэтому мы можем сказать, что площадь прямоугольника равна 6 единицам. Также мы знаем, что стороны прямоугольника в см; следовательно, площадь прямоугольника изменится с 6 единиц на 6 см.

Мы завершили все концептуальные занятия в области прямоугольника. Далее изучим и выведем формулу площади прямоугольника.

Формула площади прямоугольника

Формула, которую мы сейчас изучим, является одной из самых простых формул в математике. Несмотря на простоту, это одна из самых мощных формул. Площадь найдена по этой формуле только от изучаемой вами таблицы до жилой комнаты.

Площадь прямоугольной формулы определяется как:

Площадь = длина x ширина или длина x дыхание

Произведение длины и ширины прямоугольника дает нам формулу площади этого прямоугольника. Пусть размер прямоугольника будет «а», а дыхание — «b»; поэтому площадь «А» записывается как 

A = a x b (квадратные единицы)

Пример: Длина прямоугольной крыши 12 м, а ширина 7 м. Найдите площадь дерева, которой можно было бы покрыть всю крышу.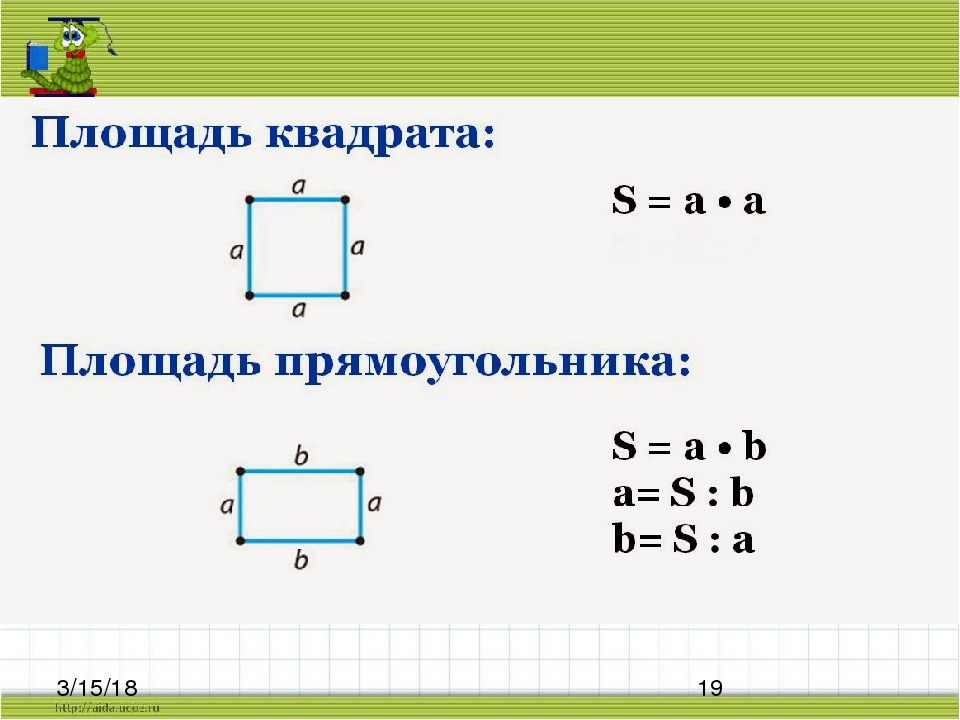

Решение: Указанная длина м ²

Теперь, когда мы узнали формулу площади прямоугольника, давайте научимся ее вычислять.

Как вычислить площадь прямоугольника?

Шаги по вычислению площади прямоугольника приведены ниже. Если вы правильно выполните эти шаги, вы никогда не получите ошибок в своих решениях.

Шаг 1: Запишите размеры данного прямоугольника из вопросов.

Шаг 2: Поместите значения в область формулы прямоугольника, т. е. длину x ширину.

Шаг 3: Умножьте значения и получите произведение.

Шаг 4: Запишите результат в квадратных единицах

Чтобы лучше понять, как вычислить площадь прямоугольника, рассмотрим следующий пример. Вычислим площадь прямоугольника длиной 20 единиц и шириной 5 единиц.

Шаг 1: Длина прямоугольника = 20 единиц, ширина прямоугольника = 5 единиц

Шаг 2: Формула площади прямоугольника = длина x ширина 100

Шаг 4: Площадь прямоугольника 100 квадратных единиц.

Доказательство площади прямоугольника?

На протяжении всей статьи мы вычисляли площадь прямоугольника как «длина × ширина». Но когда-нибудь задумывались, почему это формула? В этом разделе выведем формулу площади прямоугольника.

См. приведенный ниже рисунок. Мы видим прямоугольник KLMN с диагональю KM. Эта диагональ разделила прямоугольник на два равновеликих треугольника. Следовательно, площадь прямоугольника = 2 х площадь 1 треугольника.

Возьмем треугольник KMN. Основание KN треугольника — это длина прямоугольника, скажем, «а», а MN ширина прямоугольника — это высота треугольника, скажем, «b». Поскольку KMN является прямоугольным треугольником (поскольку смежные стороны прямоугольника перпендикулярны друг другу)

Мы знаем, что площадь треугольника равна ½ x основание x высота 

Следовательно, площадь KMN = ½ x a x b

Также , площадь прямоугольника = 2 x (площадь KMN)

                                                 = 2 x ½ x a x b

                                         = a x b 

Отсюда доказано, что площадь прямоугольника всегда равна его длине x ширине.

Предположим теперь, что нам не известны размеры длины какого-либо прямоугольника; вместо этого нам дана длина любой из диагоналей и ширина. Как узнать площадь? Узнаем в следующем разделе этой статьи.

Площадь прямоугольника по диагонали

Как упоминалось ранее, диагональ делит прямоугольник на два прямоугольных треугольника. Мы воспользуемся теоремой Пифагора, чтобы найти формулу для нахождения площади прямоугольника с помощью диагоналей.

Согласно теореме Пифагора:

(Гипотенуза) ² = (Основание) ² + (Перпендикулярная высота) ²

В этом случае:

а ширина будет ‘b’.

(диагональ) ² = (длина) ² + (ширина) ²

(D) ² = (L) ² + (b) ²

(l) ^{. 2 = (г) 2 – (б) 2}

л = √(г) ² — (B) ²

Заменить значение L в основной формуле

Площадь прямоугольника = L x B

= {(D) ² — (b) ² } x B

Таким образом, площадь прямоугольника, если известны длина одной диагонали и размер ширины, равна {(d) ² – (b) ² } x b = {(Диагональ) ² – (Ширина) ² } x Ширина 

Таким образом, вы можете использовать любой из методов, чтобы найти площадь прямоугольника в зависимости от данных, которые вам даны.

Решенные примеры для площади прямоугольника 

Пример 1. Прямоугольная ферма имеет длину и ширину 80 ярдов и 60 ярдов соответственно. Найдите площадь фермы.

Решение: 

Ферма имеет длину 80 ярдов и ширину 60 ярдов.

Площадь фермы A: A = l w

= 60 ярдов x 80 ярдов

= 4800 квадратных ярдов

В результате площадь фермы составляет 4800 квадратных ярдов.

Пример 2: Прямоугольный экран имеет длину 15 см. Его площадь составляет 180 квадратных сантиметров. Найдите его ширину.

Решение:

180 квадратных сантиметров — это размер экрана.

15 см — длина экрана.

Площадь прямоугольника = длина x ширина.

Следовательно, площадь/длина=ширине

Следовательно, ширина экрана равна 180/15, или 12 см.

Часто задаваемые вопросы

1. Что такое площадь прямоугольника в геометрии?

Ответ. Площадь прямоугольника — это простая формула, с помощью которой можно найти площадь прямоугольника. Он использует длину и ширину прямоугольника, которые являются его сторонами.

2. Какая формула площади прямоугольника?

Ответ. Формула площади прямоугольника: A = l * w, где l — длина, а w — ширина.

3. Что такое единица площади прямоугольника?

Ответ. Единицей площади прямоугольника являются квадратные метры.

4. Почему мы вычисляем площадь прямоугольника?

Ответ. Площадь прямоугольника вычисляется путем умножения ширины прямоугольника на его длину.

5. Как найти площадь прямоугольника, используя его диагональ?

Ответ. Вы можете найти площадь прямоугольника, используя его диагональ. Просто разделите количество квадратных единиц на количество диагональных единиц. Например, 4×5 имеет площадь 20 и диагональ 10, поэтому мы разделим 20 на 10, чтобы получить 2, что и является нашим ответом.

Как рассчитать площадь?

Геометрия рассматривается в школе как набор формул, отвечающих на вопрос как вычислить площадь? Геометрия — это гораздо больше: она включает в себя всю часть математики, которая решает проблемы пространства, отвечает на вопросы о форме плоских и трехмерных фигур и, она идет намного дальше, пытаясь ответить на форму нашей вселенной… Но давайте не будем заходить так далеко, прежде чем ответить на этот вопрос, важно, чтобы мы знали, что мы имеем в виду, когда спрашиваем себя о площади многоугольника.

Путаница между площадью и периметром

Когда нас спрашивают о площади, нас спрашивают о поверхности, а не о том, что ее окружает. Очень типичная путаница заключается в том, что вместо измерения или расчета поверхности мы измеряем «то, что ее окружает», периметр.

В прямоугольной картине с тонкой металлической или деревянной рамой площадь будет окрашенной частью, холстом или бумагой, а периметром будет длина рамы.

В видео ниже используется другой пример, огород с несколькими поверхностями, на которых будут высаживаться разные культуры. В их вершинах размещаются колья, а веревки ограничивают их. В этом сценарии длина этих веревок будет периметром.

Периметр всегда является мерой длины.

Видеоруководство по вычислению периметра любой фигуры

В этом видеоруководстве Smartick вы можете простым способом научиться вычислять периметр любой фигуры.

 

Прояснив, надеюсь, возможную путаницу, рекомендую прочитать: Как вычислить периметр? Если это то, что вас интересует.

Как рассчитать площадь многоугольника на сетке?

Если многоугольник, площадь которого вы хотите узнать, находится в сетке, есть очень простой способ вычислить его площадь: посчитайте квадраты, которые он покрывает. Но будьте осторожны, площади являются мерами поверхности, поэтому вы также должны указать единицы измерения. Это могут быть квадратные метры, квадратные сантиметры… они всегда будут квадратными единицами, потому что они исходят из квадратного счета, о котором мы писали.

Теперь посмотрите на следующий пример, потому что есть деталь, которую вы не можете упустить:

Под сеткой есть маленький квадратик, который говорит нам, насколько велик каждый квадрат, это легенда этой цифры и говорит нам, что каждый квадрат равен одному квадратному сантиметру .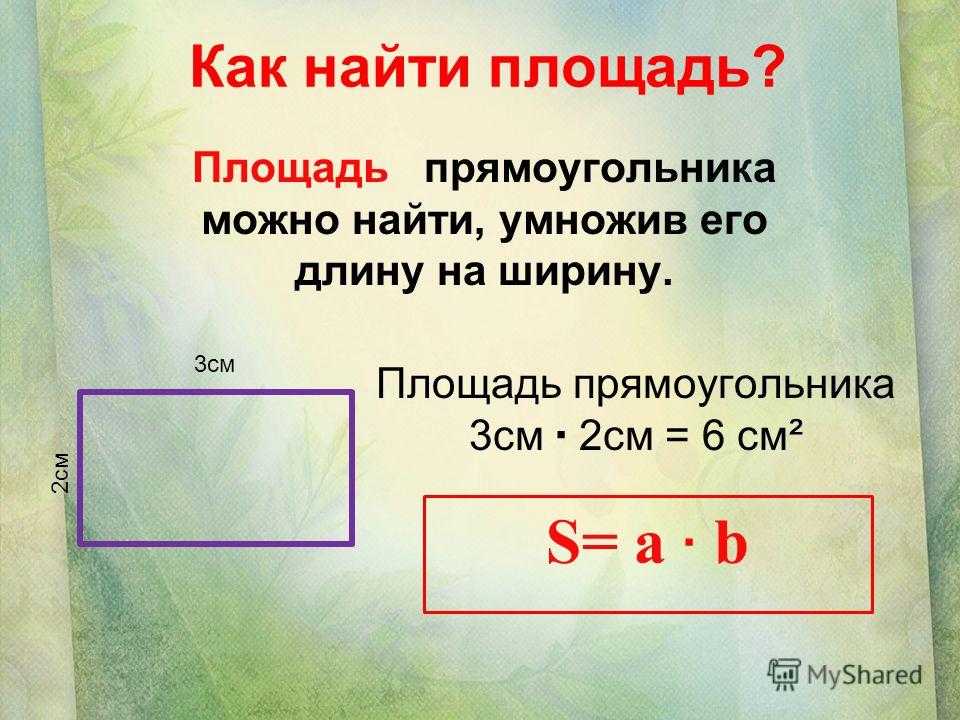 Но оно могло быть и другим и могло быть равно квадратному метру (если это был план комнаты) или квадратному километру (если это была карта региона), а могло быть так, что каждый квадрат был равен 2 см² и тогда площадь прямоугольника будет 28 на 2, 56 см².

Этот простой способ ответить на вопрос, как вычислить площадь, можно применить, когда фигура состоит из нескольких многоугольников, что называется составным многоугольником. Как в примере ниже:

В этом случае нам придется считать квадраты и полуквадраты.

Как вычислить площадь прямоугольника?

Подсчет квадратов — это хорошо, но если квадратов много, вы можете пропустить некоторые из них или пересчитать их дважды. Если фигура, площадь которой вы хотите узнать, представляет собой прямоугольник , есть более быстрый способ. Подумайте об этом, в прямоугольниках квадраты организованы в строки и столбцы. Итак, если вы хотите узнать, сколько там квадратов, вам просто нужно… умножить количество строк на количество столбцов!

Что делать, если внизу нет сетки, но вы знаете ширину и высоту прямоугольника? Ну, так как нужно было посмотреть, сколько единичных квадратов было в прямоугольнике, их будет столько, сколько произведение ширины на высоту, знаменитое основание на высоту.

Вы должны убедиться, что оба измерения находятся в одной и той же единице измерения, то есть в сантиметрах, в дециметрах, в метрах… Таким образом, вы также сможете узнать единицы площади: квадратные сантиметры, квадратные дециметры или что угодно, но квадратные.

Площадь прямоугольника= основание × высота

Как вычислить площадь прямоугольного треугольника?

Самый простой случай — прямоугольный треугольник. Вдумайтесь, прямоугольный треугольник — это половина прямоугольника, который делится своей диагональю.

Как мы уже знаем из предыдущего раздела, площадь прямоугольника вычисляется путем умножения основания на высоту, площадь треугольника будет равна половине этого произведения. Если расстояние между двумя стержнями геоплана на нашем рисунке равно 1 сантиметру, площадь прямоугольника будет 3 × 6 = 18 см², а треугольник будет иметь половину, ровно 9см².

Кстати, для рисования мы использовали этот онлайн-геоплан, на случай, если вы захотите использовать его для тестирования.

Площадь прямоугольного треугольника = (основание × высота) ⁄ 2

Эта формула будет полезна для вычисления площади и непрямоугольных треугольников, но если вы хотите узнать причину, вам придется прочитайте раздел об этом.

Как вычислить площадь ромбоида?

Ромбоид – это четырехугольник, стороны которого параллельны попарно. Как этот:

Если подумать, любой бумажный ромб можно преобразовать с помощью ножниц, вырезав прямоугольный треугольник и переместив его на противоположный конец.

Получился прямоугольник! Таким образом, прямоугольник и ромб используют один и тот же способ вычисления площади, основанной на высоте.

Площадь ромба = основание × высота

Как вычислить площадь треугольника, который не является прямоугольным?

Как остроугольные, так и тупоугольные треугольники можно рассматривать как полуромбы. Если вы скопируете и вставите треугольник рядом, вы сможете проверить его. Следовательно, и поскольку площадь ромбоида равна основанию, умноженному на высоту, площадь этих треугольников — и любого треугольника — равна основанию, умноженному на высоту, умноженную на два:

Площадь любого треугольника = (основание × высота) ⁄ 2

Как вычислить площадь трапеции?

Трапеция — это четырехугольник с двумя параллельными сторонами и двумя основаниями, как этот:

Если вы хотите узнать площадь трапеции, проще всего это сделать… то же самое мы сделали с треугольники! Просто скопируйте трапецию в сторону, и она станет ромбом!

Основание этого ромба равно сумме двух оснований трапеции, а высота остается неизменной. Таким образом, площадь ромбоида будет (основание 1 + основание 2) × высота и, поскольку трапеция является половиной ромбоида:

Площадь трапеции = [(основание 1 + основание 2) × высота] ⁄ 2

Как вычислить площадь ромба?

Ромб – это четырехугольник, у которого четыре стороны равны.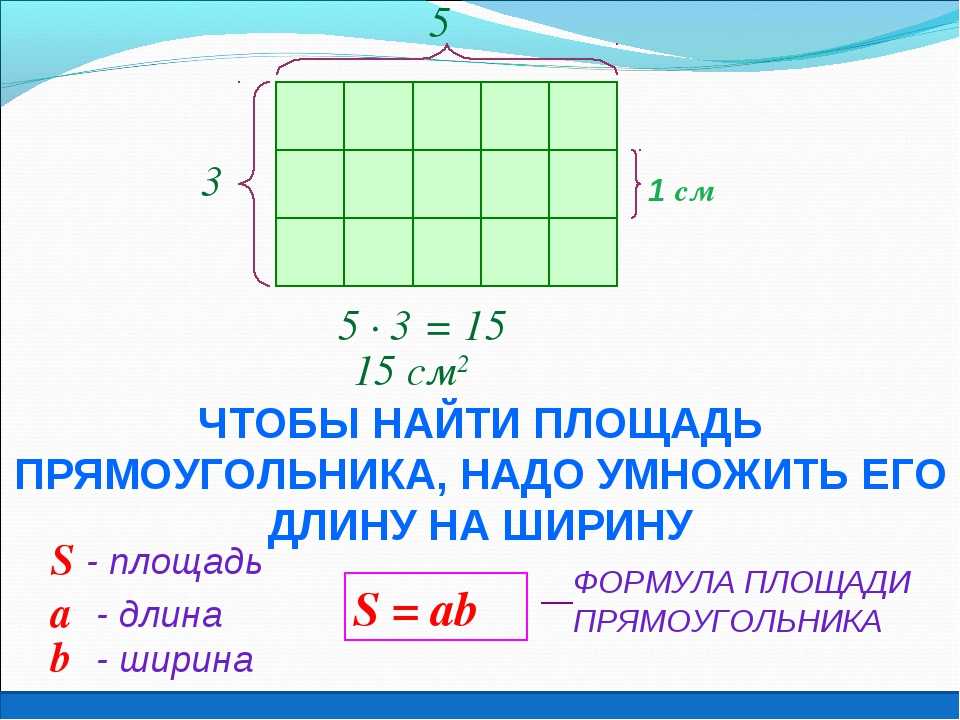 Кстати, у квадратов 4 равные стороны. Таким образом, мы можем думать о квадратах как о «предельных случаях» ромбов. Но для этой записи нас интересует ромб, который выглядит примерно так:

Чтобы вычислить площадь ромба, нужно знать длину его диагоналей. Мы будем называть D длинной диагональю, а d короткой диагональю (которые являются вертикальной и горизонтальной линиями на чертеже соответственно).

На изображении уже виден возможный способ вычисления площади ромба. Вы можете сделать это, вычислив площадь четырех одинаковых треугольников, образованных диагоналями.

Площадь любого из этих треугольников будет равна основанию, умноженному на высоту, деленному на два. Его основание составляет половину диагонали d, а высота — половину диагонали D. Следовательно, площадь одного из этих треугольников равна D, умноженному на d, деленное на 8. А так как таких треугольников у нас 4, площадь ромба равна:

Площадь ромба = (D по диагонали × d по диагонали) ⁄ 2

Как вычислить площадь правильного многоугольника с более чем 4 сторонами?

У правильного многоугольника все стороны равны, равно как и все углы. Например, посмотрите на следующий семиугольник, правильный многоугольник с 7 сторонами:

Чтобы вычислить его площадь с помощью инструментов начальной или средней школы, вам нужна длина его стороны (любой из них, они ВСЕ равны) и его апофема, которая представляет собой линию, соединяющую центр многоугольника с половиной стороны. В семиугольнике мы могли бы нарисовать 7 таких сегментов, но все они были бы одинакового размера.

Обратите внимание, что произойдет, если соединить пару последовательных вершин многоугольника с центром:

Образуется равнобедренный треугольник (в случае шестиугольника это будет равносторонний треугольник), основанием которого является сторона многоугольника и как высота апофема многоугольника. Многоугольник состоит из треугольников, равных количеству сторон, в нашем случае 7.

Площадь одного из этих треугольников будет равна стороне, умноженной на апофему, деленной на два. А так как треугольников у нас 7, то общая площадь будет 7 умножить на сторону умножить на апофему разделить на два. Но подождите, разве сторона, умноженная на 7, не будет периметром всего многоугольника? Это верно! Тогда у нас есть формула, которая не требует вычисления каждого треугольника, а затем умножения на количество треугольников:

Площадь правильного многоугольника = (периметр × апофема) ⁄ 2

Как рассчитать площадь любого неправильного или составного многоугольника?

Как мы видели в начале, если нам дан составной многоугольник или неправильный многоугольник, нам нужно будет искать части многоугольника, которые мы знаем, как вычислить, потому что у нас достаточно данных. сделать это.

Заключение

Как мы видели на протяжении всей этой длинной статьи, вычисление площадей заключается не только в изучении формул и их правильном применении, но также в рассуждениях и понимании того, что числа можно разделить на более простые. Иногда это будут стороны, иногда высоты, иногда диагонали…. Но скорее всего это будут треугольники. Треугольники — это простейшие многоугольники и ключевые элементы геометрии.