Конденсатор: формулы для конденсаторов
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
Содержание
В чем измеряется емкость конденсатора
Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.
Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны.
Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме.
Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10-12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.
Формула энергии конденсатора
С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора.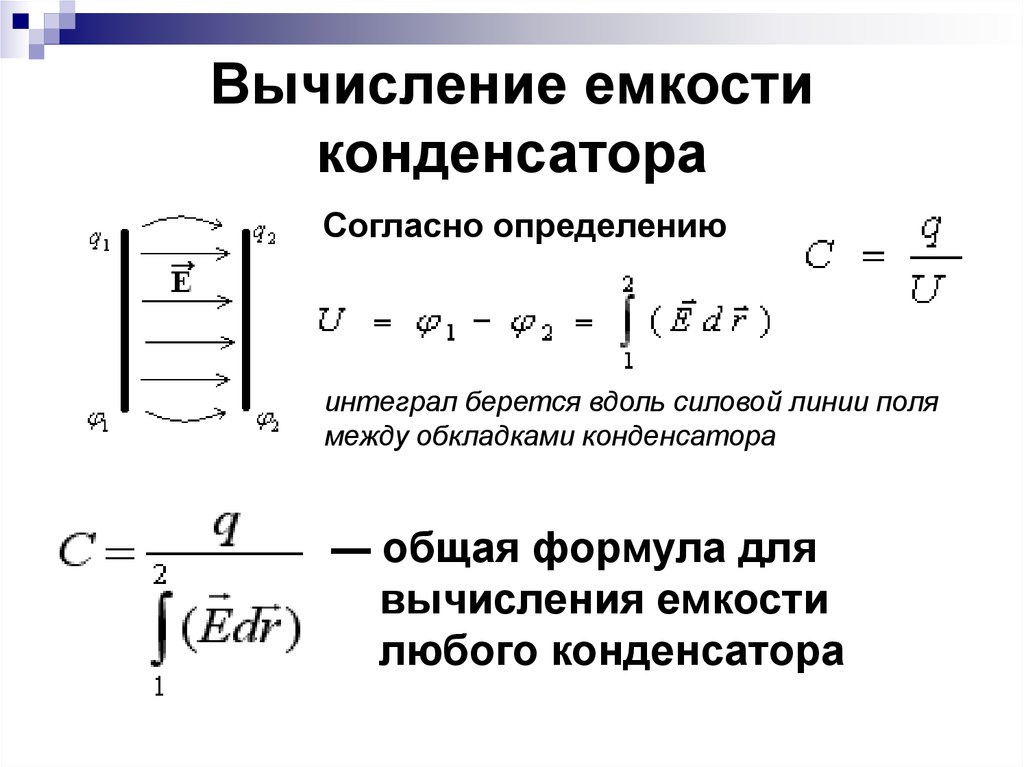
После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU2/2.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q).
Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Формула тока утечки конденсатора
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.
Основная формула для расчета выглядит следующим образом: Iут = U/Rd, где Iут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а Rd – сопротивление изоляции.
Расчет понижающего конденсатора
|
|
|
|||||||||||||||||||||||||||||||||||||
334146654694E-5 Фарад 
Угол между ними.
Матрица смежности онлайнКонденсатор i-v уравнение в действии
Конденсатор является одним из идеальных элементов цепи.
Давайте применим уравнение для конденсатора $i$-$v$, чтобы увидеть, что произойдет с напряжением, если мы добавим ток.
Автор Вилли Макаллистер.
Содержимое
- Реакция напряжения на импульс тока
- Перед импульсом
- Во время импульса
- После импульса
- Всего ответов
- Имитационная модель
- Задача дизайна
Куда мы движемся
Постоянный ток, подаваемый в конденсатор, создает напряжение с прямолинейным нарастанием. Такое поведение предсказывается интегральной формой уравнения конденсатора $i$-$v$.
Обычное уравнение конденсатора $i$-$v$ представляет собой зависимость $i$ от $v$ в производной форме,
$i = \text C \,\dfrac{dv}{dt}$
$\text C$ — это емкость , физическое свойство конденсатора. $\text C$ — это масштабный коэффициент, который говорит вам, сколько $i$ вы получите за заданное количество $dv/dt$.
9{\,T} i\,dt + v_0$
$v_0$ — напряжение на конденсаторе в начале интеграла, при $t=0$.
Обозначение времени немного сложное,
Маленький $t$ — непрерывная временная переменная внутри интеграла.
Большой $T$ — это момент, когда вы хотите узнать напряжение на конденсаторе. $T$ — верхний предел интеграла.
$i = \text C\,\dfrac{dv}{dt}$
$d$ — это исчисление для «дифференциала» или «маленького изменения в…». Например, $dt$ означает «мизерное изменение во времени». Когда вы видите его в соотношении, таком как $dv/dt$, это означает «крошечное изменение $v$ (напряжения) для каждого крошечного изменения $t$ (времени)». Выражение, подобное $dv/dt$, производная. Производная измеряет скорость изменения напряжения во времени (наклон напряжения в зависимости от времени). 9{\,T} i\,dt + v_0$
Петля $\int$ — еще один символ исчисления. Это интегральный признак. Его значение аналогично символу суммирования Sigma $\Sigma$.
Интегрирование противоположно взятию производной.
В уравнении конденсатора знак интеграла означает, что вы складываете последовательность произведений $(i \times dt)$ или (current $\times$ крошечный интервал времени). Когда вы видите верхний и нижний пределы символа интеграла, это делает его определенным интегралом . Это означает интегрировать по определенному диапазону $t$. Вы начинаете в момент времени $t=0$ и останавливаетесь в момент времени $t=T$. 9{\,T} i\,dt + v_0$
Текущий импульс имеет резкие изменения, поэтому мы собираемся найти $v(t)$ в трех отдельных фрагментах: до, во время и после текущего импульса.
Перед импульсом
Перед импульсом тока $(t < 0)$ ток не течет, поэтому на $\text C$ не накапливается заряд. Следовательно, $v_{(t<0)} = 0$. Нам даже не пришлось использовать уравнение.
Во время импульса
В любое время в течение импульса тока $(0 \lt t \lt 3\,\text{ms})$ протекает ток, на $\text C$ накапливается заряд, а напряжение возрастает.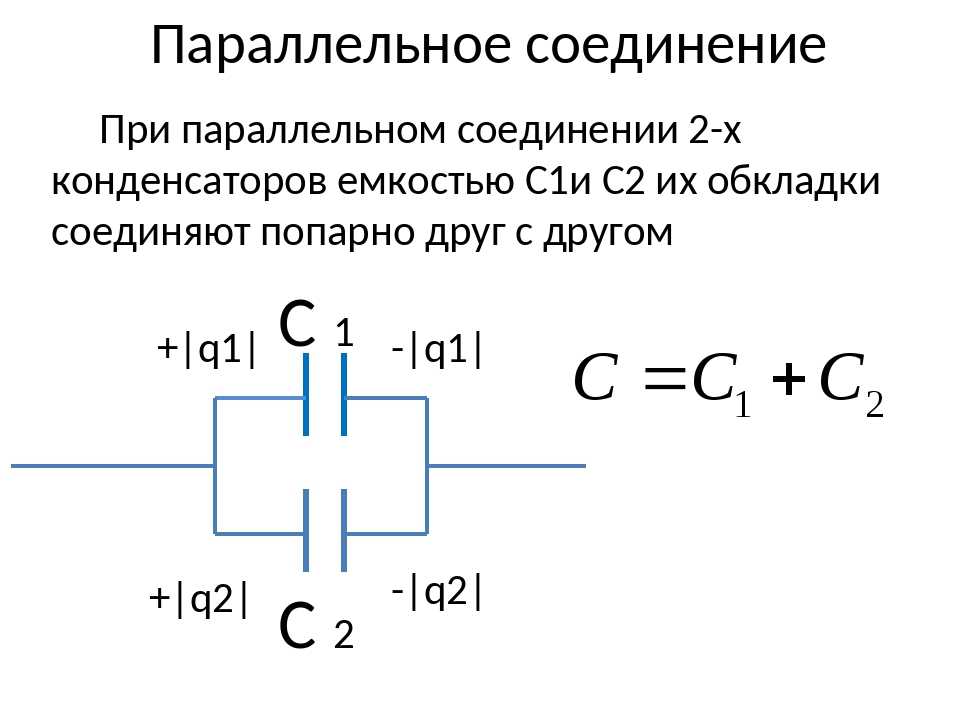
Примените уравнение конденсатора, чтобы найти, что происходит с напряжением, 9{\,T} i\,dt + v_0$
Обратите внимание на временные переменные. Маленький $t$ — это непрерывное время, переменная, которая интегрируется. Большой $T$ — это время, в течение которого может накапливаться заряд. Определенный интеграл пролистывает время $t$ от $0$ до некоторого времени накопления, большого $T$. Чтобы найти напряжение в конце импульса, присвоим большой $T$ значение $3\,\text{ms}$.
$i$ постоянна (вершина импульса плоская) в течение этого времени, поэтому мы можем вынести ее за пределы интеграла. Мы сказали, что конденсатор начал с заряда $0$, поэтому $v_0$ равен нулю, и мы можем его не указывать. 9{-6}\,\text F} = 2000\,\text{вольт/сек}$
Для любой ширины импульса напряжение равно,
$v(T) = 2000 \,\text{вольт/сек } \,\cdot T$
Ширина нашего импульса $T = 3\,\text{ms}$, поэтому напряжение на конденсаторе возрастает до,
$v_{(T=3\,\text{ms })} = 2000 \,\text{вольт/сек} \,\cdot \,0,003 \,\text{сек} = 6\,\text{вольт}$
При постоянном токе $2\,\text {мА}$, напряжение на конденсаторе нарастает по прямой с наклоном $2000\,\text{вольт/сек}$.
Напряжение начиналось с $0\,\text V$ и поднималось до $6\,\text{volts}$ после $3\,\text{ms}$.
После импульса
Эта часть довольно интересна, если вы не задумывались об этом раньше. После импульса ток падает до $0$. Это означает, что заряд перестает накапливаться на конденсаторе. Это может показаться странным, но поскольку заряд не движется, заряду, накопленному на конденсаторе, некуда деваться, поэтому он остается на конденсаторе. Это означает, что мы должны ожидать, что напряжение на конденсаторе останется прежним. $q = \текст C\,v$. Константа $q$ подразумевает константу $v$.
Посмотрите, как математика фиксирует это, написав уравнение конденсатора после окончания импульса. 9{\,T} 0\,dt + 6$
Интеграл оценивается как $0$, и мы получаем,
$v(T) = 6\,\text V\quad$ для любого значения $T$.
После прекращения тока заряд сохраняется, поэтому напряжение на конденсаторе остается постоянным на уровне $6\,\text В$. Он остается там навсегда.
Общий отклик
Объединение трех фрагментов дает нам $v(t)$ на нижнем графике,
Эта конфигурация схемы (источник тока, питающий конденсатор) имеет прозвище.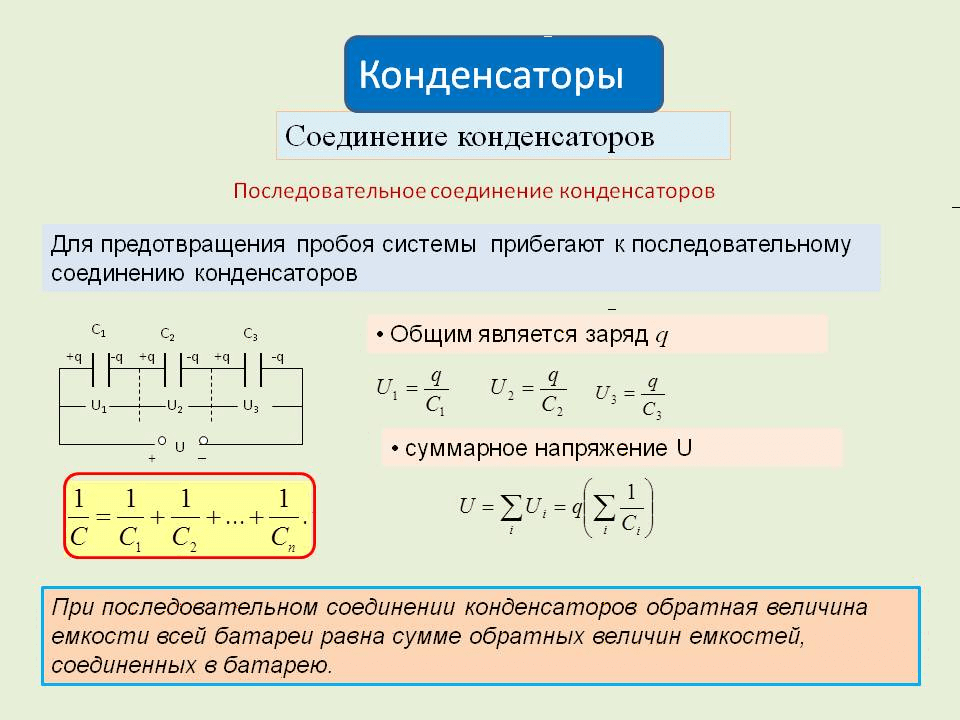
Это называется интегратор , потому что он накапливает или интегрирует заряд с течением времени. Он часто используется для создания пилообразного напряжения.
Имитационная модель
Найдите ток и напряжение с помощью этой имитационной модели. Откройте ссылку и щелкните TRAN в верхней строке меню, чтобы выполнить переходную симуляцию. Источник тока моделируется как одиночный ИМПУЛЬС. (Дважды щелкните текущий источник, чтобы увидеть, как он определяется.) Элементы управления масштабированием находятся в левой части окна и отображаются светло-серым цветом.
Вот еще одна имитационная модель с источником тока, определенным другим способом, как форма волны PWL (кусочно-линейная). Время и ток вводятся в виде списка разделенных запятыми пар [время, ток], например: -1 с, 0, 0 с, 0, 1 нс, 2 м, 3 мс, 2 м, 3 мс, 0, 5 с, 0.
Посмотрите, можете ли вы изменить форму кривой тока, чтобы напряжение на конденсаторе снизилось до $0\text V$ еще за $3\,\text{ms}$.
Вы собираетесь сделать что-то похожее на это:
Дважды щелкните текущий источник и введите это в PWL «список чередующихся значений времени и значений, разделенных запятыми».
-1с,0,0с,0,1нс,2м,3мс,2м,3мс,-2м,6мс,-2м,6мс,0,10с,0
Источник тока заряжает конденсатор в течение $3\,\text{мс}$, и напряжение нарастает. Затем он меняет направление, чтобы снять заряд еще на $3\,\text{ms}$. Напряжение представляет собой другое линейное изменение, на этот раз с отрицательным наклоном, поскольку заряд удален.
Резюме
Если подать постоянный ток на конденсатор, он создаст напряжение, имеющее прямолинейную форму. Мы использовали интегральную форму уравнения конденсатора $i$-$v$, чтобы предсказать это.
Подход к решению этой схемы — хороший пример того, как инженеры разбивают проблему на мелкие части, решая каждую простую часть и заново собирая полный ответ. Первым вашим побуждением при столкновении с такой сложной проблемой должно быть: «Как я могу порубить это на кусочки?»
RC-цепи
RC-цепиРЦ Цепи
RC-цепь
просто схема с резистором и конденсатором.
Этот
комбинация полезна для изучения, потому что конденсаторы могут быть использованы для
накапливать энергию, а резистор, помещенный вместе с конденсатором, может
контролировать скорость, с которой энергия высвобождается из конденсатора.
Мы ограничим нашу исследования к следующему типу RC-цепи.
Переключатель можно перемещать с позиции a на позицию b . Прежде чем идти дальше, давайте рассмотрим некоторые факты о конденсаторах:
заряд конденсатора не может измениться мгновенно . С момента смены ответственного D Q = I D t , должны всегда быть ненулевым временем, прежде чем заряд сможет изменить ненулевое количество, если только не было бесконечного тока.
Есть отсутствует ток через конденсатор в установившемся режиме . Поскольку заряд накапливается на конденсаторе, а не течет через него ток может накапливаться до тех пор, пока напряжение V=Q/C уравновесит внешнее напряжение подталкивает заряд к конденсатору.
При наличии конденсатора емкостью С последовательно с батареей напряжением В б и резистор сопротивлением R , падение напряжения должно быть:
,
, который является заявлением о том, что
напряжение, полученное на аккумуляторе, должно равняться напряжению
падение на конденсаторе плюс падение напряжения на
резистор. Уравнение, в котором скорость изменения величины (Д В/ Д т )
пропорциональна количеству (D Q) всегда будет иметь
экспоненциальное решение.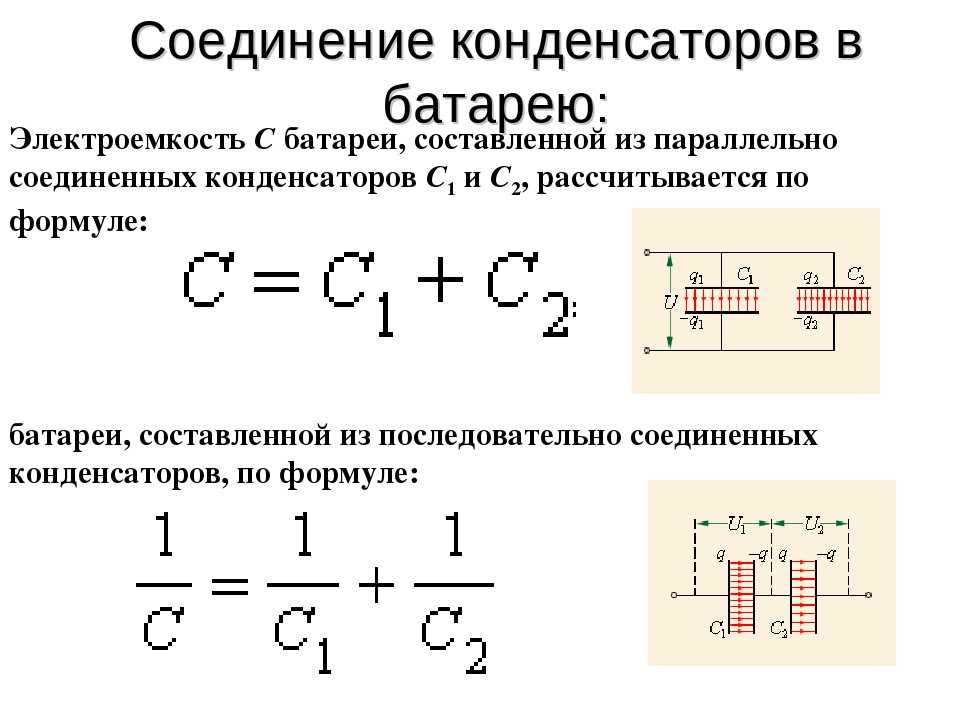
Рассматриваем два экземпляра:
Разгрузка конденсатор : Конденсатор изначально подключен (переключатель в положении и ) в течение длительного времени, а затем отключается путем перемещения переключиться на б по времени т = 0 . Затем конденсатор разряжается, оставляя конденсатор без заряда или напряжения после длительного время.
Зарядка конденсатор : Переключатель находится в положении b в течение длительного времени, позволяя конденсатору чтобы не было заряда. В момент времени t = 0 , переключатель меняется на и и конденсатор заряжается.
| Разгрузка | Зарядка | |
| Плата | ||
| Текущий | ||
| Напряжение |
Здесь, Q 0 , В 0 и I 0 ток и напряжение заряда
конденсатор в момент после нажатия выключателя.
Время t является характеристикой
время распада, t = RC . При столкновении с RC проблема, лучшая стратегия следующая:
Решите, какая плата через конденсатор был непосредственно перед переключением брошенный. Так как заряд не может измениться мгновенно, это это заряд сразу после того, как переключатель брошен.
Решите, какая плата долгое время после того, как переключатель брошен.
Выберите экспоненту форма для сбора Q(t) , чтобы удовлетворить правильный начальный и конечный обвинения.
Напряжение на конденсатор можно найти через, V = Q/C . Напряжения на других элементах можно найти с помощью с помощью первого закона Кирхгофа.
