Площадь круга через диаметр или радиус, калькулятор онлайн
Калькулятор площади круга
Варианты расчёта площади круга через радиус или диаметр
Выбираем вариант расчёта площади
РадиусДиаметрВизуально выглядит так:
Вводим диаметр или радиус:
Площадь круга равна :
Рассчитать
Площадь круга с радиусом r равна πr2. Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к её диаметру или площади круга к квадрату его радиуса. Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть 1⁄2 × 2πr × r).
Википедия
Как рассчитать площадь круга по диаметру или радиусу, формулы
Найти площадь круга по диаметру или радиусу можно в нашем онлайн калькуляторе. Расчёты можно производить в любых единицах, в метрах(м), дециметрах(дцм), сантиметрах(см), миллиметрах(мм). Просто вводим цифры и получаем результат.
Расчёты можно производить в любых единицах, в метрах(м), дециметрах(дцм), сантиметрах(см), миллиметрах(мм). Просто вводим цифры и получаем результат.
Условные обозначения в формулах
- S- площадь окружности
- Р- число п = 3,14159
- R- радиус окружности
- D- диаметр окружности D=2R
Формула расчёта через радиус
S=Р*R2
Формула расчёта через диаметр
S=1/4Р*D2
Что такое площадь круга, как с ней работать.
Круг от руки нарисовать не получиться, рисуют круг с помощью циркуля, но циркуль был не всегда. В самом начале ещё до того как появился циркуль, обычно использовали какую-то верёвку. Как делают, круг начинается с какой-то точки, это называется центр круга. Круг всегда начинается с этой точки по центру.
Окружность она равноудалена от центра поэтому мы берём расстояние, замеряем, и берём верёвку равную этой длине. Обычно верёвку прибивали прямо на землю или ещё куда-то, очень четко фиксировали и чертили круг.
Чтобы так не мучиться, придумали циркуль, с помощью циркуля это делается легко и просто. Расстояние от центра до линии круга оно везде одинаковое, это расстояние называется радиус.
Ещё есть число Пи, многие его знают как 3,14. Что это за число и откуда оно взялось мы говорить не будем в этой статье. Площадь считается как число Пи умножить на радиус в квадрате. Чтобы посчитать площадь круга, нам всего-навсего нужно знать радиус, потому что число Пи всегда известно.
Давайте какой-нибудь пример разберём. Например у нас есть радиус длиной 3 м, и вот у нас получился круг у которого радиус 3 метра, как мы тогда будем считать площадь. Площадь равна Пи умножить на радиус в квадрате, радиус равен трём.
Нам нужно найти площадь, тогда мы берём нашу формулу
S=Пи х r2
где S- площадь; Пи= 3,14; r- радиус.
Подставляем пи 3,14 и R-радиус равен трём и в квадрат. Что значит в квадрате, это значит 3 умножается сама на себя, 3х3=9
Как посчитать, 3 на 3 будет 9 и потом только умножаем на 3,14. В результате получаем 28,26- это и есть площадь круга.
В результате получаем 28,26- это и есть площадь круга.
Вычислить радиус
Дата публикации: 21-09-2015 10:21:21 / Дата изменения: 28-09-2015 20:10:33
Вычислить радиус достаточно нетрудно. В интернете много сервисов предлагающих услуги по его расчету. Вот и сайт «Все обо Всем» решил создать свой собственный сервис для подобных расчетов. Но, прежде чем говорить о самом сервисе, давайте напомним, что такое радиус и как проводить вычисление радиуса в математике.
Вычислить радиус при помощи сервиса «Все обо всем».
Другие статьи на эту тему:
Вычислить диаметр.
Вычислить длину окружности.
Вычислить площадь круга.
Вычислить площадь шара.
Вычислить объем шара.
Радиус круга (шара) – это отрезок, который соединяет центр круга или шара с точкой на его поверхности. Мы начнем нашу статью с самого простого вида расчета радиуса – расчет радиуса по известной величине диаметра круга (шара).
Вычисление радиуса по диаметру.
Для начала вычисления нужно иметь представление о том, что такое диаметр круга или шара. Диаметр – это отрезок, который соединяет две точки, лежащие на окружности или поверхности шара и проходящий через его центр. Диаметр делит круг на два ровных полукруга. Для вычисления диаметра применяют следующую формулу: D=2r. Из этой формулы следует, что радиус равен r=D/2.
Вычислить радиус по длине окружности.
Дадим определение длине окружности. Длинна окружности – это кривая линия, все точки которой лежать на одинаковом и максимальном удалении от центра круга. Для расчета длинны окружности используют следующую формулу L=2Pr.
Вычислить радиус по площади круга.
Для вычисления площади круга используют формулу S=Pr2. Остается вопрос, как вычислить радиус, основываясь на имеющихся данных о площади круга. Выразим значение радиуса из площади круга. Радиус равен квадратному корню из площади деленной на постоянную P. r=√ S/P.
Вычислить радиус по площади шара.
Площадь шара, так же как и все, приведенные в этой статье характеристики тесно связана с его радиусом. Расчет площади шара при известном радиусе осуществляется по следующей формуле: S=4Pr2. Из этой формулы можно без проблем вывести формулу для получения радиуса: r=√S/4P.
Вычислить радиус по объему шара.
У многих посетителей нашего сайта возникает проблема с вычислением радиуса шара по известному показателю его объема. И это не удивительно, ведь здесь имеют место самые сложные вычисления. К счастью, наш сервис достаточно умен и проводит все расчеты в считанные секунды. Итак, давайте узнаем по какой формуле вычисляется объем шара? Формула имеет следующий вид: V=4/3(Pr3). Формула не представляет из себя ничего сверх сложного, однако получить из нее значение радиуса не так уж и просто. Формула для расчета радиуса из объема шара имеет следующий вид: r=ᶟ√(V/(3/4P)). Радиус равен кубическому корню из объема шара деленного на три четвертых Пи.
И это не удивительно, ведь здесь имеют место самые сложные вычисления. К счастью, наш сервис достаточно умен и проводит все расчеты в считанные секунды. Итак, давайте узнаем по какой формуле вычисляется объем шара? Формула имеет следующий вид: V=4/3(Pr3). Формула не представляет из себя ничего сверх сложного, однако получить из нее значение радиуса не так уж и просто. Формула для расчета радиуса из объема шара имеет следующий вид: r=ᶟ√(V/(3/4P)). Радиус равен кубическому корню из объема шара деленного на три четвертых Пи.
Вот такая у нас получилась образовательная статья по вопросу вычисления радиуса, надеюсь, Вам было интересно. В ближайшее время Вас ожидает еще ряд статей на тему вычисления диаметра, длинны окружности, площади круга, площади шара и объема шара.
Другие статьи на эту тему:
Вычислить диаметр.
Вычислить длину окружности.
Вычислить площадь круга.
Вычислить площадь шара.
Вычислить объем шара.
Калькулятор круга и шара. Рассчитать радиус, диаметр, длину окружности, площадь круга и шара, объем шара онлайн.
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr2. Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
S=4Pr2. Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr3). Она была использована при создании нашего онлайн сервиса. Сайт tellaboutall.ru дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга.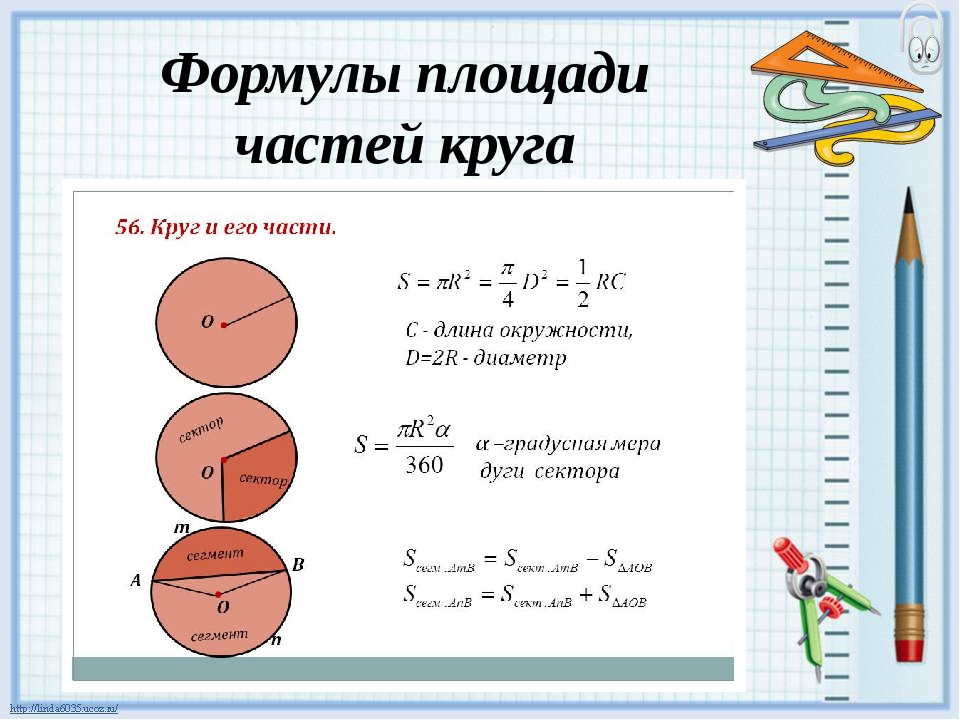 Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Калькулятор для расчета площади различных геометрических фигур
Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:
Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.
Полезные калькуляторы
Расчет площади прямоугольника
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади треугольника
Способ нахождения площади треугольника: По трем сторонамПо одной стороне и высоте, опущенной на эту сторонуПо двум сторонам и углу между ними
Вычислить
Результат:
S= 1111
кв. ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади параллелограмма
Способ нахождения площади параллелограмма:
По основанию и высоте параллелограммаПо двум сторонам и углу между нимиПо двум диагоналям и углу между ними
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади правильного многоугольника
Многоугольник с числом сторон n и длиной стороны аМногоугольник с числом сторон n, вписанный в окружность радиуса RМногоугольник с числом сторон n, описанный вокруг окружности радиуса r
Вычислить
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади круга
Рассчитать площадь круга, если известен:
Результат:
S= 1111
кв.
Расчет площади эллипса
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади сектора круга
Рассчитать площадь сектора круга, если известен:
|
r= ммсммкмфутярддюйммиля |
|
|
θ= ммсммкмфутярддюйммиля град.рад. |
Результат:
S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Расчет площади трапеции
Способ нахождения площади треугольника: По двум основаниям a,b и высоте hПо двум основаниям a,b и боковым сторонам c,d
Результат:
S= 1111
кв. ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.
| Метрические единицы измерения площади: | |
| Квадратный метр, производная единица системы СИ 1 м2 = | 1 са (сантиар) |
| Квадратный километр — 1 км2 = | 1 000 000 м2 |
| Гектар — 1 га = | 10 000 м2 |
| Ар (сотка) — 1 а = | 100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м) |
| Квадратный дециметр, 100 дм2 = | 1 м2; |
| Квадратный сантиметр, 10 000 см2 = | 1 м2; |
| Квадратный миллиметр, 1 000 000 мм2 = | 1 м2. |
Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.
Площадь круга все формулы и примеры расчета
Автор Ольга Андрющенко На чтение 2 мин. Просмотров 2.5k. Опубликовано
Площадь круга часто требуется рассчитать в различных задачах и это не только задачи по геометрии, иногда знать как рассчитывается площадь круга важно знать и в некоторых текстовых задачах алгебры. Итак, давайте разбираться.
Что такое площадь круга
Площадь круга — это мера заполненности области внутри окружности, являющейся границей круга, выраженная в квадратных единицах (м2, см2, кв.ед.). В математике эти единицы могут разными, в физике же если вы определяете площадь круга — вы должны указать единицы в системе СИ, а это м2.
Визуально, площадь круга это величина закрашенной области на рисунке:
Как можно найти площадь круга
Если дан радиус круга
Здесь все зависит от того, какие вам величины даны в самом начале. Если вам дан радиус круга, то площадь круга определяется по формуле:
— число . Число пи является одним из наиболее важных констант в математике, определяется как постоянное отношение длины окружности к ее диаметру в евклидовой плоскости. Другими словами:
π = длина окружности круга/диаметр этого круга.
Таким образом, приблизительное значение , наиболее известное, как: 3,14.
Это приблизительное значение, потому что число π — это то, что мы называем иррациональным числом. Оно не может быть записано как отношение двух целых чисел. Сегодня мы знаем более 12 000 миллиардов знаков после запятой. Однако до сих пор нет определенной модели, которая давала бы все эти значения.
Если дан диаметр круга
Если известен диаметр круга, то площадь круга можно найти по формуле:
Если дана длина окружности
Так как длина окружности определяется по формуле: , то можно выразить радиус круга: . Тогда площадь: .
Тогда площадь: .
Примеры расчета
Пример 1.
Рассчитать площадь круга, если известен радиус круга .
Решение: По формуле (1) находим .
Пример 2.
Найдите площадь, если дан диаметр круга .
Решение: По формуле (2) находим .
Вы видите, что находить площадь круга совсем не сложно, если известны все формулы и даны все необходимые для расчета величины.
Формула нахождения площади сечения — Морской флот
В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса.
Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Цилиндр, конус и шар — базовые объемные фигуры.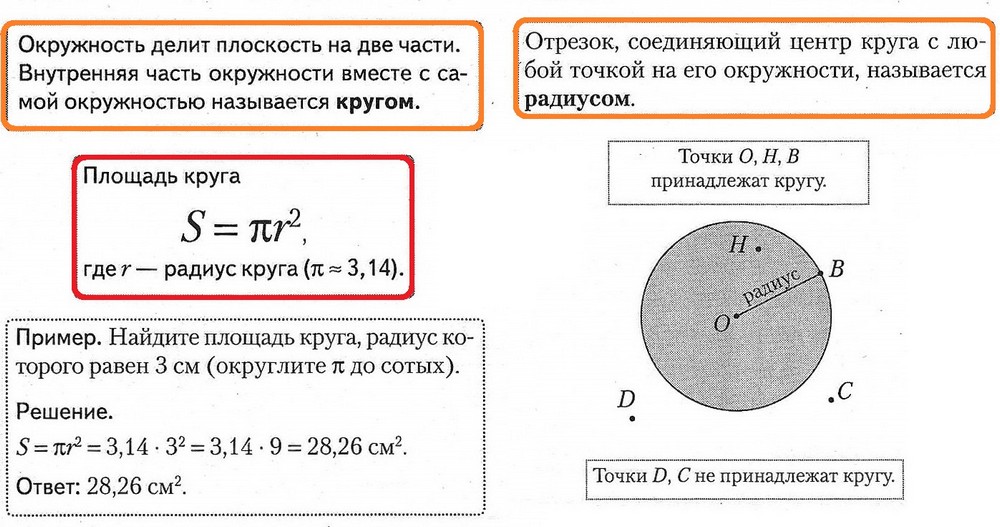 Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.

- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
- Как вычислить площадь сечения
- Как находить площадь круга
- Как найти сечение провода
- Линейка, карандаш, ластик.
- как найти площадь получившейся фигуры
Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).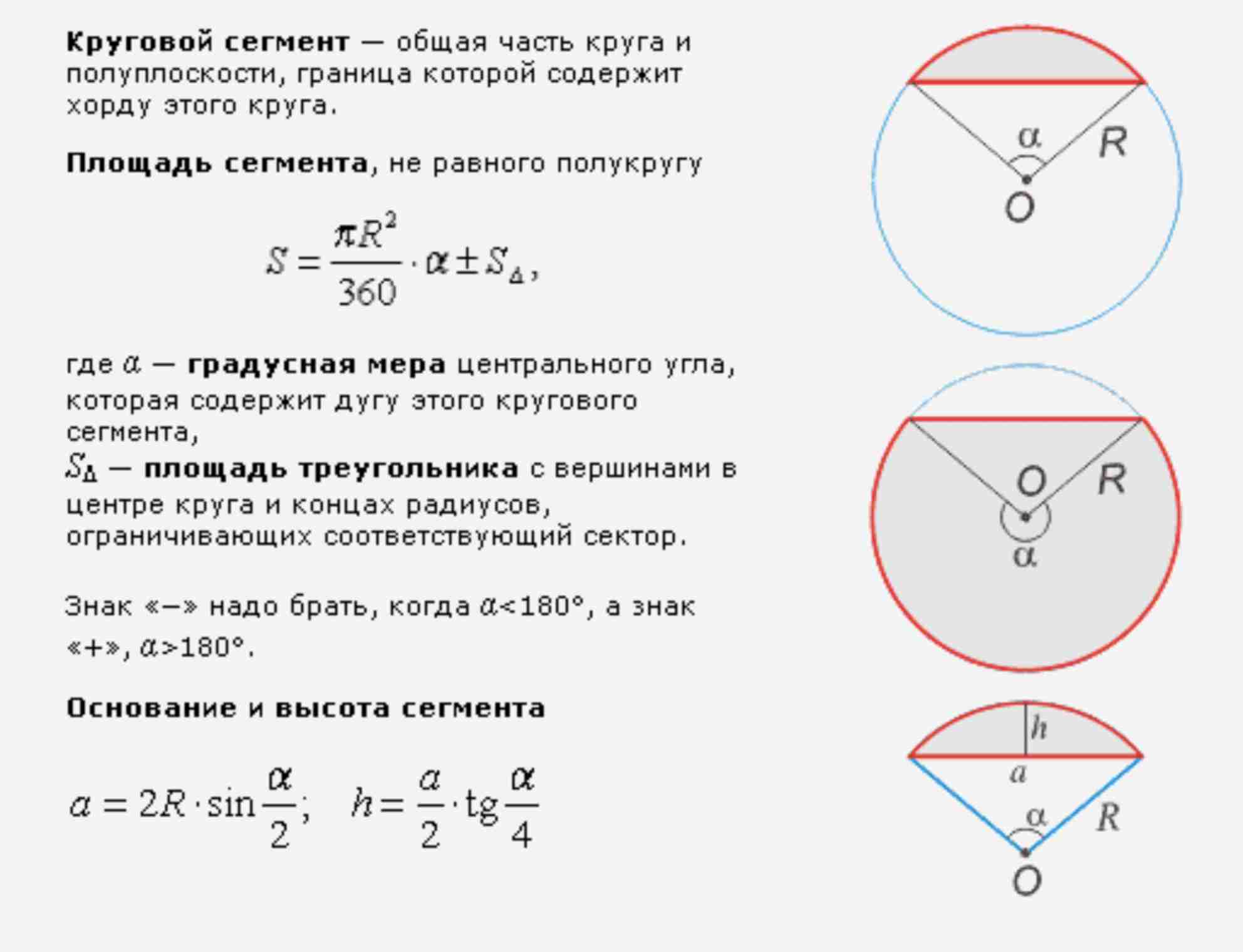
Радиус круга – отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга – отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса
или радиус круга или длину окружности, можно найти его площадь.
r – радиус круга
D – диаметр круга
Формула площади круга, (S):
на тему: Площадь круга
Калькулятор для расчета площади круга через радиус
Калькулятор для расчета площади круга через диаметр
L – длина окружности
О – центр круга
Формула площади круга если известна длина окружности, (S):
на тему: Площадь круга
Калькулятор для расчета площади круга через длину
онлайн-калькулятор расчета через радиус, диаметр и длину окружности
С помощью нашего онлайн калькулятора можно найти площадь круга зная его радиус, диаметр, длину окружности.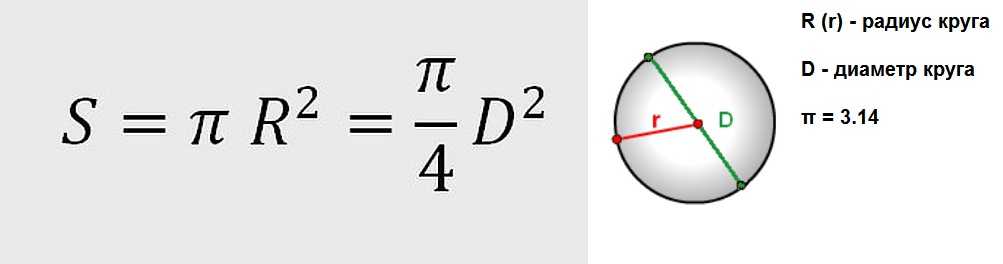
3 основных формулы площади круга:
👉через радиус — S=πR².
👉через диаметр — S=¼πd².
👉через длину окружности — .
Через радиус
S=πR²
Через диаметр
S=¼πd²
Через длину окружности
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
- r – радиус круга.
- d – диаметр круга.
- π (греческая буква пи) всегда равно 3,14 — обозначает константу, выражающую отношение длины окружности к его диаметру или площади круга к квадрату его радиуса.
Чтобы окончательно разобраться в теме «Круг и его площадь», смотрите видео урок на котором учитель математики понятно рассказывает все, что вам нужно знать.
Оцени статью
ОценитьСредняя оценка / 5. Количество голосов:
Спасибо, помогите другим — напишите комментарий, добавьте информации к статье.
Или поделись статьей
Видим, что вы не нашли ответ на свой вопрос.
Помогите улучшить статью.
Напишите комментарий, что можно добавить к статье, какой информации не хватает.Отправить
Спасибо за ваши отзыв!
Калькулятор площади круга
Калькулятор площади круга помогает вычислить поверхность круга с учетом диаметра или радиуса . Наш инструмент работает в обоих направлениях. — неважно, ищете ли вы для расчета площади или радиуса для площади , вы нашли нужное место ◔
Наш инструмент работает в обоих направлениях. — неважно, ищете ли вы для расчета площади или радиуса для площади , вы нашли нужное место ◔
Мы познакомим вас с наиболее важной информацией, касающейся площади круга, его диаметра и радиуса.Мы научимся , как найти площадь круга , поговорим о , формуле площади круга , и обсудим другие разделы математики, в которых используется то же уравнение.
Как рассчитать площадь круга? Формула площади круга
Итак, давайте посмотрим, как найти площадь круга. Есть несколько способов добиться этого. Здесь мы можем вычислить площадь круга , используя диаметр или , используя радиус .
| 💡 Диаметр — это линия, которая пересекает центр фигуры и касается обоих ее краев.Радиус начинается в центре фигуры и заканчивается на краю фигуры. |
Диаметр круга можно найти, умножив радиус круга на два:
Диаметр = 2 * Радиус
Площадь окружности радиуса. В калькуляторе радиуса круга используется следующая формула площади круга:
В калькуляторе радиуса круга используется следующая формула площади круга:
Площадь круга = π * r 2
Площадь диаметра круга. Калькулятор диаметра круга использует следующее уравнение:
Площадь круга = π * (d / 2) 2
Где:
- π примерно равно 3,14 . Неважно, хотите ли вы найти площадь круга, используя диаметр или радиус — вам нужно будет использовать эту константу почти в каждом случае.
Теперь, когда вы знаете, как рассчитать площадь круга, мы рекомендуем вам попробовать другие наши калькуляторы кругов:
> Сектор круга — это сечение круга между двумя радиусами.Вы можете думать об этом как о гигантском куске пиццы. > Это «отрезанная» часть круга, ограниченная хордой или секущей. > Это угол с вершиной в центре, руки которого доходят до окружности.Как использовать калькулятор площади круга? Диаметр к площади и радиус к площади.
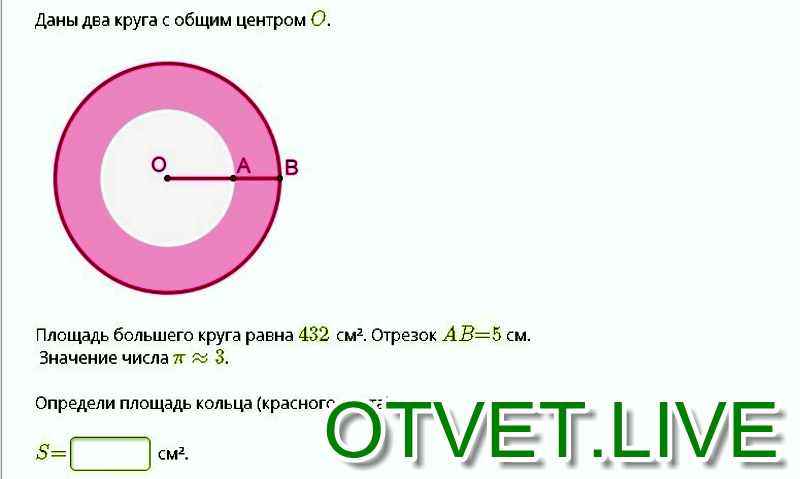
Вы можете легко вычислить все, площадь круга, его диаметр и радиус, , используя наш калькулятор площади круга в мгновение ока:
Определите , является ли ваше заданное значение диаметром или радиусом , используя изображение справа и определения, доступные в разделе выше (вы можете рассчитать площадь круга, используя диаметр, а также радиус) .
Введите значение в соответствующее поле калькулятора .
Это не заняло много времени — ваши результаты здесь ! Мы решили включить пошаговое решение и все самые важные данные прямо под калькулятор.
Вот как быстро вычислить площадь круга 😉
Зачем нам нужны калькуляторы площади круга?
Площадь круга, определенная калькуляторами радиуса и диаметра , служит основой для многих других уравнений — не только в математике, но и в повседневной жизни! Вот несколько примеров, когда знание того, как найти площадь круга, может быть полезно:
Нам нужно знать площадь поверхности круга, чтобы рассчитать объем конуса и его площадь 🎉
Ваша вечеринка с пиццей была бы неполной без нашего инструмента для пиццы на основе калькулятора диаметра к площади 🍕
Мы используем вычисления, подобные этому, при получении информации о сфере, например, об объеме сферы.
 🌐
🌐Вам нравятся красивые платья? Может вы любите шить ? Откройте для себя наш калькулятор для круглой юбки! Эффективное шитье еще никогда не было таким простым. 👗
Площадь круга
Калькулятор
Введите радиус , диаметр, окружность или площадь Окружности, чтобы найти остальные три. Расчеты производятся «вживую»:
images / circle-dia-circ.js
Как рассчитать площадь
Площадь круга:
или, если известен диаметр: A = (π / 4) × D 2
или, если вы знаете Окружность: A = C 2 / 4π
Пример: Какова площадь круга радиусом 3 м?
Радиус = r = 3
Площадь = π r 2
= π × 3 2
= 3.14159 … × (3 × 3)
= 28,27 м 2 (до 2 знаков после запятой)
Как помнить?
Чтобы помочь вам запомнить, подумайте «Пирог в квадрате»
(хотя пироги обычно круглые )
Сравнение круга с квадратом
Интересно сравнить площадь круга с квадратом:
Круг имеет около 80% площади квадрата такой же ширины.
Фактическое значение (π / 4) = 0.785398 … = 78,5398 …%
Почему? Поскольку площадь квадрата составляет w 2
, а площадь круга составляет (π / 4) × w 2
Пример: Сравните квадрат с кругом шириной 3 м
Площадь квадрата = w 2 = 3 2 = 9 м 2
Оценка площади круга = 80% площади квадрата = 80% от 9 = 7,2 м 2
Истинная площадь круга = (π / 4) × D 2 = (π / 4) × 3 2 = 7.07 м 2 (до 2 знаков после запятой)
Оценка 7,2 м 2 не за горами 7,07 м 2
Пример «Реальный мир»
Пример: Макс строит дом. Первый шаг — просверлить отверстия и залить их бетоном.
Отверстия шириной 0,4 м и глубиной 1 м , сколько бетона Макс должен заказывать для каждого отверстия?
Отверстия круглые (в поперечном сечении), потому что высверливаются с помощью шнека.
Диаметр 0,4 м, значит Площадь:
A = (π / 4) × D 2
A = (3,14159 … / 4) × 0,4 2
А = 0,7854 … × 0,16
A = 0,126 м 2 (до 3 знаков после запятой)
А ямки глубиной 1 м, итак:
Объем = 0,126 м 2 × 1 м = 0,126 м 3
So Max должен заказать 0,126 кубометра бетона для заполнения каждой дыры.
Примечание: Макс мог иметь по оценке площади по:
- 1.Расчет квадратного отверстия: 0,4 × 0,4 = 0,16 м 2
- 2. Принимая 80% этого (примерный круг): 80% × 0,16 м 2 = 0,128 м 2
- 3. А объем скважины глубиной 1 м составляет: 0,128 м 3
И кое-что интересное для вас:
См. Площадь круга по линиям
Калькулятор кругов
Укажите любое значение ниже, чтобы рассчитать оставшиеся значения круга.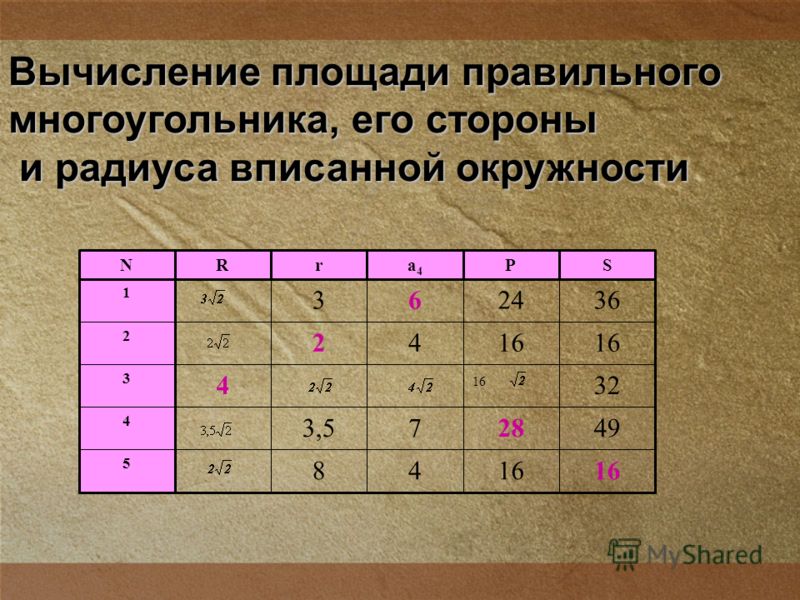
В то время как круг символически представляет множество разных вещей для множества разных групп людей, включая такие понятия, как вечность, безвременье и тотальность, круг по определению представляет собой простую замкнутую форму. Это набор всех точек на плоскости, которые равноудалены от данной точки, называемой центром. Его также можно определить как кривую, очерченную точкой, где расстояние от данной точки остается постоянным при перемещении точки. Расстояние между любой точкой круга и центром круга называется его радиусом, а диаметр круга определяется как наибольшее расстояние между любыми двумя точками на окружности.По сути, диаметр в два раза больше радиуса, так как наибольшее расстояние между двумя точками на окружности должно быть отрезком прямой, проходящим через центр окружности. Окружность круга может быть определена как расстояние вокруг круга или длина контура вдоль окружности. Все эти значения связаны через математическую константу π, или пи, которая представляет собой отношение длины окружности к ее диаметру и составляет приблизительно 3,14159. π — иррациональное число, означающее, что оно не может быть выражено в точности как дробь (хотя часто приближается к 22/7), а его десятичное представление никогда не заканчивается или имеет постоянный повторяющийся узор.Это также трансцендентное число, означающее, что оно не является корнем любого ненулевого многочлена с рациональными коэффициентами. Интересно, что доказательство Фердинанда фон Линдеманна в 1880 году, что π трансцендентно, наконец положило конец тысячелетнему поиску «квадратуры круга», начатому древними геометрами. Это включало попытку построить квадрат с той же площадью, что и данный круг, за конечное количество шагов, только с использованием циркуля и линейки. Хотя сейчас известно, что это невозможно, и представление о пылких усилиях взволнованных древних геометров, пытающихся сделать невозможное при свете свечей, может вызвать смехотворный образ, важно помнить, что именно благодаря таким людям многие математические концепции являются правильными. определено сегодня.
π — иррациональное число, означающее, что оно не может быть выражено в точности как дробь (хотя часто приближается к 22/7), а его десятичное представление никогда не заканчивается или имеет постоянный повторяющийся узор.Это также трансцендентное число, означающее, что оно не является корнем любого ненулевого многочлена с рациональными коэффициентами. Интересно, что доказательство Фердинанда фон Линдеманна в 1880 году, что π трансцендентно, наконец положило конец тысячелетнему поиску «квадратуры круга», начатому древними геометрами. Это включало попытку построить квадрат с той же площадью, что и данный круг, за конечное количество шагов, только с использованием циркуля и линейки. Хотя сейчас известно, что это невозможно, и представление о пылких усилиях взволнованных древних геометров, пытающихся сделать невозможное при свете свечей, может вызвать смехотворный образ, важно помнить, что именно благодаря таким людям многие математические концепции являются правильными. определено сегодня.
Формулы круга
D = 2R С = 2πR А = πR 2 | где: R: радиус |
Площадь круга Калькулятор
- Цель использования
- Вычислить, насколько больше пиццы находится в XL против большого.
[1] 2021/04/19 06:51 Мужчина / 30-летний уровень / Другое / Немного /
- Цель использования
- Чтобы определить силу натяжения ремня цепи печи, в котором используются воздушные цилиндры
[2] 2021/02/07 11:37 Мужчина / Уровень 50 лет / Инженер / Очень /
- Цель использования
- Немедленное получение ответа ОК
- Комментарий / запрос
- Я могу найти такие единицы, как см. Дюйм, метр, мм.
Можете прояснить, все в порядке, цифровой ответ в порядке, хорошо
[3] 2021/01/10 00:03 Мужчина / Уровень 50 лет / Инженер / Немного /
- Цель использования
- определение базовой поверхности голландских духовок, чтобы решить, нужно ли мне увеличивать время приготовления, когда я удваиваю рецепт
[4] 2020/12/17 02:13 Мужчина / 60 лет и старше / Самостоятельно занятые люди / Очень /
- Цель использования
- круги и геометрия
- Комментарий / запрос
- Мне нравятся читос! А еще я люблю завязывать шнурки! пойти по магазинам с моим старым папой, он еще жив! А я люблю стирать одежду
[5] 2020/12/10 07:02 Мужчина / 60 лет или старше / Инженер / Совсем нет /
- Цель использования
- Чтобы узнать, можете ли вы произнести больше, чем эти цифры числа Пи.
- Комментарий / запрос
- Это больше, чем я могу. Спасибо!
[6] 2020. 10.27 07:16 Мужчина / До 20 лет / Начальная школа / Младший школьник / Очень /
10.27 07:16 Мужчина / До 20 лет / Начальная школа / Младший школьник / Очень /
- Цель использования
- Для расчета внутренней площади геодомной теплицы.
- Комментарий / запрос
- Очень полезный сайт — большое спасибо!
[7] 2020/10/24 23:38 Женский / 20-летний уровень / Старшая школа / Университет / аспирант / Очень /
- Цель использования
- Помогло мне найти области круга.
[8] 2020/10/08 18:09 Мужской / До 20 лет / Начальная школа / Младший школьник / Полезно /
- Цель использования
- определение площади деревянного шнура
[9] 2020/09/16 02:24 Женщины / возраст 60 лет и старше / Самостоятельно занятые лица / Полезные /
- Цель использования
- сравнение площади круглой водопропускной трубы и площади прямоугольной водопропускной трубы, и предоставить распечатку заинтересованному землевладельцу.

[10] 2020/08/26 00:40 Мужчина / 60 лет и старше / Офисный работник / Государственный служащий / Очень /
Площадь круга — пояснения и примеры
Напомним, что область — это область, занимающая фигуру в двухмерной плоскости.В этой статье вы узнаете площадь круга и формулы для расчета площади круга.
Какова площадь круга?
Площадь круга — это мера пространства или области, заключенной внутри круга. Проще говоря, площадь круга — это общее количество квадратных единиц внутри этого круга.
Например, , если вы рисуете квадраты размером 1 см на 1 см внутри круга. Тогда общее количество полных квадратов, расположенных внутри круга, представляет площадь круга.Мы можем измерить площадь круга в м 2 , км 2 , в 2 , мм 2, и т. Д.
Формула площади круга
Площадь круга можно рассчитать по трем формулам . Эти формулы применяются в зависимости от предоставленной вам информации.
Давайте обсудим эти формулы для определения площади круга.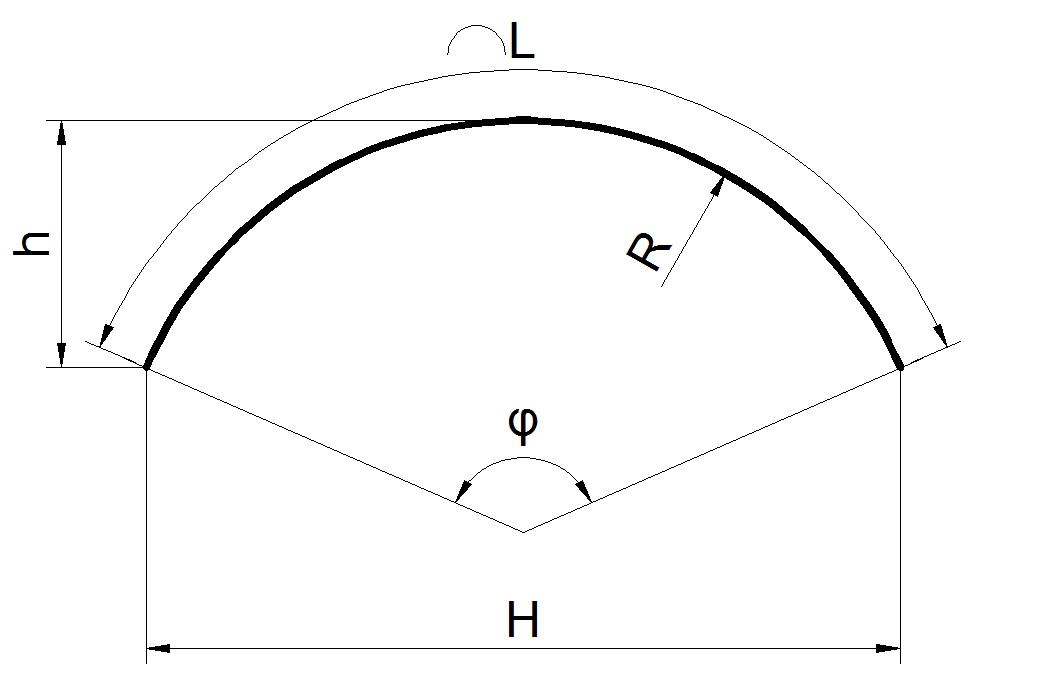
Площадь круга с использованием радиуса
Учитывая радиус круга, формула для вычисления площади круга утверждает, что:
Площадь круга = πr 2 квадратных единиц
A = πr 2 квадратных единиц
Где A = площадь круга.
пи (π) = 22/7 или 3,14 и r = радиус круга.
Давайте лучше поймем эту формулу, решив несколько примеров задач.
Пример 1
Найдите площадь круга радиусом 15 мм.
Раствор
A = πr 2 квадратных единиц
По замене,
A = 3,14 x 15 2
= (3,14 x 15 x 15) мм 2
= 706.5 мм 2
Итак, площадь круга 706,5 мм 2
Пример 2
Рассчитайте площадь круга, показанного ниже.
Раствор
A = πr 2 квадратных единиц
= (3,14 x 28 2 ) см 2
= (3,14 x 28 x 28) см 2
= 2461,76 см 2
Пример 3
Площадь круга 254.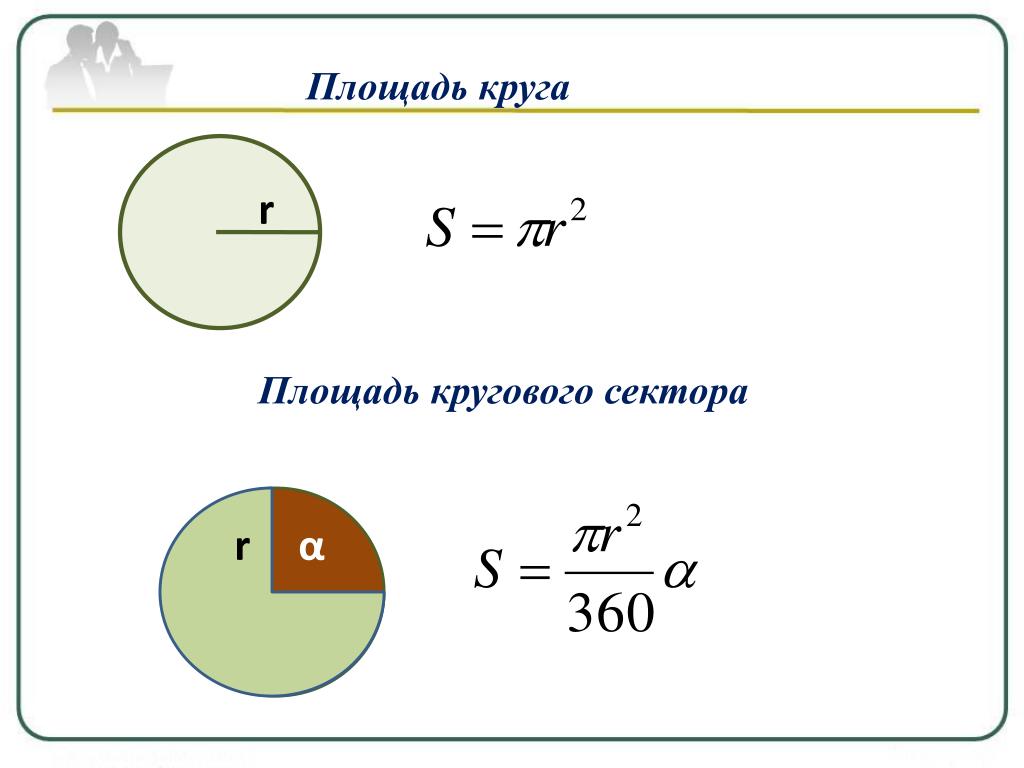 34 квадратных ярда. Каков радиус круга?
34 квадратных ярда. Каков радиус круга?
Раствор
A = πr 2 квадратных единиц
254,34 = 3,14 x r 2
Разделите обе стороны на 3,14.
r 2 = 254,34 / 3,14 = 81
Найдите квадратный корень из обеих частей.
√r 2 = √81
г = -9, 9
Так как радиус не может иметь отрицательного значения, мы принимаем положительное 9 за правильный ответ.
Итак, радиус круга равен 9 ярдам.
Пример 4
Дождеватель лужайки разбрызгивает воду на 10 футов во всех направлениях при вращении. Какова площадь засыпанного газона?
Раствор
Здесь радиус 10 футов.
A = πr 2 квадратных единиц
= 3,14 х 10 2
= (3,14 x 10 x 10) кв. Футов
= 314 кв. Футов
Таким образом, площадь засыпанного газона составляет 314 кв. Футов.
Площадь круга диаметром
Если диаметр круга известен, площадь круга определяется выражением
.
Площадь круга = πd 2 /4 квадратных единицы
Где d = диаметр круга.
Пример 5
Найдите площадь круга диаметром 6 дюймов.
Раствор
A = πd 2 /4 квадратных единицы
= 3,14 х 6 2 /4 кв. дюймы.
= (3,14 х 6 х 6) / 4 кв. в дюймах
= 28,26 кв. Дюймов
Итак, площадь круга диаметром 6 дюймов составляет 28,26 квадратных дюймов.
Пример 6
Рассчитайте площадь круга, показанного ниже.
Раствор
Учитывая диаметр,
A = πd 2 /4 квадратных единицы
= 3,14 х 50 2 /4
= (3,14 х 50 х 50) / 4
= 1962,5 см 2
Пример 7
Вычислите площадь обеденной тарелки диаметром 10 см.
Раствор
A = πd 2 /4 квадратных единицы
= 3,14 x 10 2 /4
= (3. 14 х 10 х 10) / 4
14 х 10 х 10) / 4
= 78,5 см 2
Пример 8
Диаметр круглой тарелки 20 см. Найдите размеры квадратной тарелки, которая будет иметь ту же площадь, что и круглая тарелка.
Раствор
Приравнять площадь круга к площади квадрата
πd 2 /4 = с 2
3,14 x 20 2 /4 = s 2
с 2 = 314
Найдите квадратный корень из обеих частей, чтобы получить,
с = 17.72
Следовательно, размеры квадратной тарелки будут 17,72 см на 17,72 см.
Пример 9
Найдите диаметр круга площадью 156 м 2 .
Раствор
А = πd 2 /4
156 = 3,14d 2 /4
Умножьте обе стороны на 4.
624 = 3,14d 2
Разделите обе стороны на 3,14.
198,726 = d 2
д = 14. 1 мес.
1 мес.
Таким образом, диаметр круга будет 14,1 м.
Площадь круга по окружности
Как мы уже знаем, длина окружности — это расстояние по окружности. Можно вычислить площадь круга по его длине.
Площадь круга = C 2 / 4π
А = С 2 / 4π
Где C = длина окружности.
Пример 10
Найдите площадь круга, длина окружности которого равна 25.12 см.
Раствор
Учитывая окружность,
Площадь = C 2 / 4π
A = 25,12 2 / 4π
= 50,24 см 2
Пример 11
Какова длина окружности окружности 78,5 мм 2 ?
Раствор
А = С 2 / 4π
78,5 = С 2 / 4π
Умножаем обе стороны на 4π.
С 2 = 985.96
Найдите квадратный корень из обеих частей.
C = 31,4 мм.
Итак, длина окружности 31,4 мм.
Предыдущий урок | Главная страница | Следующий урокПлощадь круга | Формула для радиуса, диаметра и окружности
Содержание
- Какова площадь круга?
- Как найти площадь круга
Какова площадь круга?
Круг — это не квадрат, а площадь круга (количество внутреннего пространства, заключенного в круг) измеряется в квадратных единицах.Найти площадь квадрата несложно: длина умножена на ширину.
У круга, однако, есть только диаметр , или расстояние в поперечнике. У него нет четко видимой длины и ширины, поскольку круг (по определению) — это набор всех точек, равноудаленных от данной точки в центре.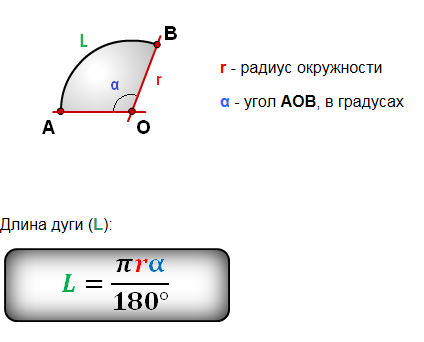
Тем не менее, имея только диаметр или половину диаметра (радиус ), или даже только длину окружности (расстояние вокруг), вы можете вычислить площадь любого круга.
Как найти площадь круга
Напомним, что отношение длины окружности к ее диаметру всегда одно и то же, 3.14159265, пи или π. Это число π, умноженное на квадрат радиуса круга, дает вам площадь внутренней части круга в квадратных единицах.
Формула площади круга
Если вам известен радиус r в любых единицах измерения (мм, см, м, дюймы, футы и т. Д.), Используйте формулу π r 2 , чтобы найти площадь, A:
Ответом будут квадратные единицы линейных единиц, такие как мм2, см2, м2, квадратные дюймы, квадратные футы и так далее.
Вот круг радиусом 7 метров. Какая у него площадь?
[вставить чертеж круга шириной 14 м с обозначенным радиусом 7 м]
А = π · r2
А = π × 72
А = π × 49
A = 153,9380 м2
Площадь круга с использованием диаметра
Если вам известен диаметр d в любых единицах измерения, возьмите половину диаметра, чтобы получить радиус r в тех же единицах.
Вот комплекс недвижимости Сан-Сити, штат Аризона, круглого города диаметром 1.07 километров. Какой район Сан-Сити?
Сначала найдите половину заданного диаметра, чтобы получить радиус:
1,072 = 0,535 км = 535 м
Подставьте радиус в нашу формулу:
А = π · r2
А = π × 5352
A = π × 286,225
A = 899 202,3572 м2
Чтобы преобразовать квадратные метры, м2, в квадратные километры, км2, разделите на 1000000:
A = 0,8992 км2
Самый западный круглый жилой комплекс Сан-Сити имеет площадь почти 1 квадратный километр!
Как рассчитать площадь круга
Попробуйте эти вычисления площади для четырех разных кругов.Будь осторожен; некоторые указывают радиус r, а некоторые — диаметр d.
Не забудьте взять половину диаметра, чтобы найти радиус, прежде чем возводить радиус в квадрат и умножать на π.
Проблемы
- A Велосипедное колесо диаметром 406 мм
- Колесо обозрения «Лондонский глаз», радиус 60 метров
- Велосипедное колесо диаметром 26 дюймов
- Самая большая пицца в мире имела радиус 61 фут 4 дюйма (736 дюймов)
Не ищите ответов, пока не произведете расчеты!
ответов
- Велосипедное колесо диаметром 406 мм имеет радиус r 203 мм:
- Радиус 60 метров колеса обозрения «Лондонский глаз»:
- Велосипедное колесо диаметром 26 дюймов имеет радиус r 13 дюймов:
- Самая большая пицца в мире с радиусом 736 дюймов:
А = πr2
A = π × 203 мм2
А = 637.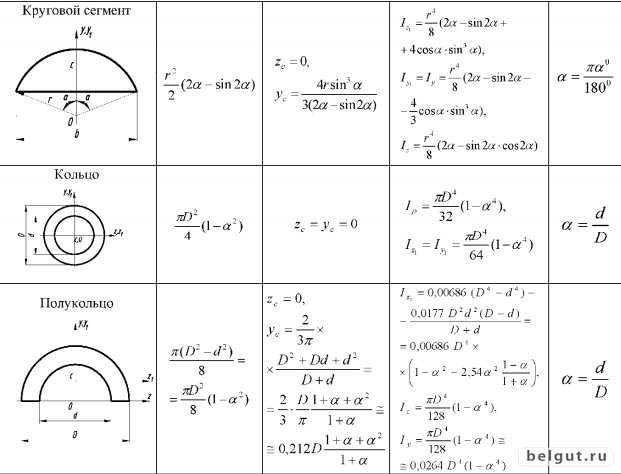 7433 мм2
7433 мм2
А = πr2
A = π × 60 м2
A = 188,4955 м2
А = πr2
A = π × 13 дюймов2
A = 530,9291 дюйм2
А = πr2
A = π × 736 дюйм2
A = 1 701 788,17 дюйм2
То есть 11817.97 квадратных футов пиццы! Ням! В любом случае, как вы справились с четырьмя задачами?
Площадь круга по окружности
Если вы не знаете, что такое радиус или диаметр, но знаете длину окружности C, вы можете все же найти площадь.
Формула площади и окружности
Окружность (расстояние по окружности) находится по следующей формуле:
С = 2πr
Это означает, что мы можем взять формулу окружности и «решить для r», что даст нам:
г = C2π
Мы можем заменить r в нашей исходной формуле этим новым выражением:
А = π C2π2
Это выражение упрощается до следующего:
Эта формула работает каждый раз!
Как найти область по окружности
Вот красивая пиццы разумного размера , которую вы можете разделить с тремя друзьями. Вы знаете, что окружность вашей пиццы составляет 50,2655 дюйма, но вы не знаете ее общую площадь. Вы хотите знать, сколько квадратных дюймов пиццы вам понравится.
Вы знаете, что окружность вашей пиццы составляет 50,2655 дюйма, но вы не знаете ее общую площадь. Вы хотите знать, сколько квадратных дюймов пиццы вам понравится.
[вставить мультяшный рисунок типичной 16-дюймовой пиццы, но не указывать диаметр]
Замените C в формуле на 50,2655 дюйма:
А = 50,265524π
А = 2,526,62044π
A = 201,0620 дюйм2
Поровну разделите эту общую площадь для полноразмерной пиццы между четырьмя друзьями, и каждый получит 50.2655 дюйм2 пиццы! Это примерно треть квадратного фута на каждого из вас! Ням ням!
Следующий урок:
Площадь сектора круга
Калькулятор площади круга Найдите и вычислите CDAR
Как рассчитать окружность, диаметр, площадь и радиус Калькулятор окружности находит площадь, радиус, диаметр и длину окружности, обозначенной как a, r , d и c соответственно.
Этот калькулятор круга предназначен для тех, кто испытывает трудности с использованием формул вручную для определения площади, длины окружности, радиуса и диаметра круга.Уравнения будут приведены ниже, чтобы вы могли видеть, как калькулятор получает значения, но все, что вам нужно сделать, это ввести основную информацию. Все остальное сделает калькулятор.
Окружность похожа на периметр в том смысле, что это общая длина, необходимая для рисования окружности.
Обозначим окружность как c .
c = 2 πr
или
c = πd
Это зависит от того, знаете ли вы радиус ( r ) или диаметр ( d )
Давайте например, рассчитать вручную.
Если r = 6 см, длина окружности равна c = 2 π (6) = 12 π см, если писать через π. Если вы предпочитаете числовое значение, ответ, округленный до десятых, составит 37,7 см.
Допустим, вам известен только диаметр? Если диаметр равен 8 см, то окружность равна c = π (8) = 8 π или 25,1 см с округлением до ближайшей десятой.
Формулы хороши тем, что вы можете манипулировать ими, чтобы найти неизвестное, если вам известна одна из других величин.Например, если нам известна длина окружности, но неизвестен радиус, вы можете решить c = 2 πr для r и получить \ (r = \ frac {c} {2 \ pi} \) . Аналогично, если вам нужен диаметр по окружности, просто возьмите c = πd и решите относительно d, чтобы получить d = \ (\ frac {c} {\ pi} \).
@mometrixFinding the Area:Нужна помощь в поиске площади круга? Мы вас прикрыли! Ссылка в биографии. ## math ## mathhelp ## Mathematics ## piday ## pi ## mometrix ## area
♬ оригинальный звук — Mometrix Test Preparation
Пусть a = площадь круга
a = πr²
Если вам известен диаметр, а не радиус, просто разделите диаметр на 2, чтобы получить радиус, и по-прежнему используйте формулу выше.

 Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
 🌐
🌐