Как рассчитать площадь земельного участка неправильной формы?
Опубликовано: 04.03.2018
Время на чтение: 5 мин
3251
Площадь – важнейшая характеристика земельного участка. Этот показатель необходим при уплате земельного налога или совершении какой-либо сделки с землей.
СодержаниеПоказать
- Расчет площади участка
- Вариант оценки
- Выводы
Расчет площади участка
Поскольку площадь является одной из основных характеристик участка, то ее величина приводится в составе данных регистрируемого в ЕГРН участка. Эта площадь вычисляется по сложным формулам кадастровым инженером в процессе проведения межевания. Однако в некоторых случаях желательно оценить площадь участка на местности.
Для определения площади участка, имеющего простую форму в виде геометрической фигуры типа треугольника, квадрата или прямоугольника, можно использовать простейшие формулы аналитической геометрии. Порядок определения площади участка, имеющего форму неправильного четырехугольника, зависит от типа такого многоугольника.
На местности наиболее просто произвести замеры длин границ участка с помощью рулетки. Вычислить площадь участка при этом можно вычислить по формуле Брахмагупты:
S=√(p-a)*(p-b)*(p-c)*(p-d),
где а, b, c и d – длины границ участка, а p=0,5*(a+b+c+d) – половина его периметра.
Но такая формула верна только в том частном случае, когда фигура, отображающая форму участка (четырехугольник) может быть вписана в окружность. А это означает, что суммы противоположных углов четырехугольника должны быть равны между собой и равны 180°.
В других случаях для определения площади участка четырехугольной формы необходимо измерять и углы.
Например, если известны длины диагоналей фигуры (l1 и l2) и угол между ними φ, то площадь участка равна:
S=0,5* l1* l2*sin φ.
Если условие применения формулы Брахмагупты не выполняется (четырехугольник нельзя вписать в окружность), то используется более общий вид формулы:
S=√(p-a)*(p-b)*(p-c)*(p-d) –a*b*c*d*cos2(α+β)/2,
где α и β – противолежащие углы.
Из приведенных формул видно, что информации о четырех измеренных границах участка в форме четырехугольника для вычисления его площади недостаточно. В любом случае необходимо оценить величины противоположных углов.
Если можно вписать в четырехугольник окружность с радиусом r, то площадь участка будет равна:
S=p*r.
Вариант оценки
Вариантом определения площади участка четырехугольной формы с помощью измерений одной рулеткой является разбиение четырехугольника на 2 треугольника. После измерения сторон участка (a, b, c, d) и одной из диагоналей (l1), площади треугольников S1 и S2 можно определить по формуле Герона:
S1=√(p1-a)*(p1-d)*(p1- l1),
где p1=0,5*(a+d+l1) – половина периметра первого треугольника.
S2=√(p2-b)*(p2-c)*(p2- l1),
где p2=0,5*(b+c+l1) – половина периметра второго треугольника.
Тогда площадь всего участка будет равна площадей треугольников:
S= S1+ S2.
Выводы
- Определить площадь участка четырехугольной неправильной формы только по длинам его границы нельзя. Необходима информация об углах четырехугольника.
- Для оценки площади участка такой формы можно использовать вариант с разбиением его на две фигуры треугольной формы. При этом дополнительно к измерениям сторон участка необходимо измерить одну из диагоналей, соединяющих противоположные опорные точки участка.
Вверх
Как найти площадь по длине и ширине. Калькулятор расчета площади земельного участка неправильной формы
Одна из первых формул, которая изучается в математике, связана с тем, прямоугольника. Она же является и самой часто используемой. Прямоугольные поверхности окружают нас повсюду, поэтому часто требуется знать их площади. Хотя бы для того, чтобы узнать, хватит ли имеющейся в наличии краски для покраски полов.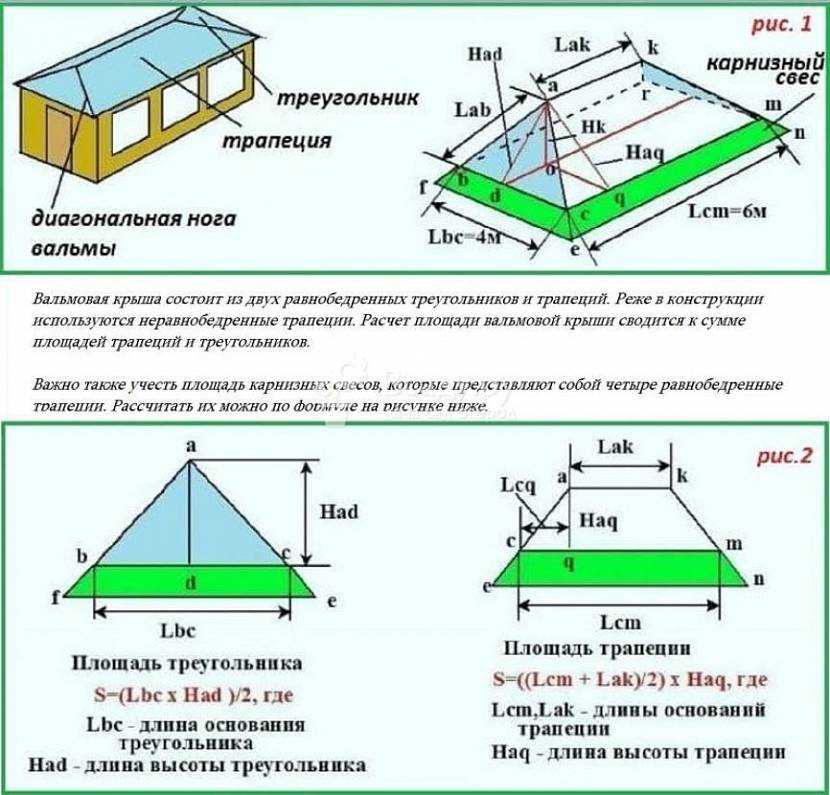
Какие единицы измерения площади существуют?
Если говорить о той, которая принята за международную, то это будет квадратный метр. Его удобно использовать при расчете площадей стен, потолка или пола. В них указывается площадь жилья.
Когда речь идет о меньших предметах, то вводят квадратные дециметры, сантиметры или миллиметры. Последние нужны, если фигура не больше ногтя.
При измерении площади города или страны самыми подходящими оказываются квадратные километры. Но есть еще и единицы, которые используют для того, чтобы указать размер площади: ар и гектар. Первая из них еще называется соткой.
Как быть, если заданы стороны прямоугольника?
Подобным образом рассчитывается который является частным случаем прямоугольника. Так как у него все стороны равны, то произведение становится квадратом буквы а .
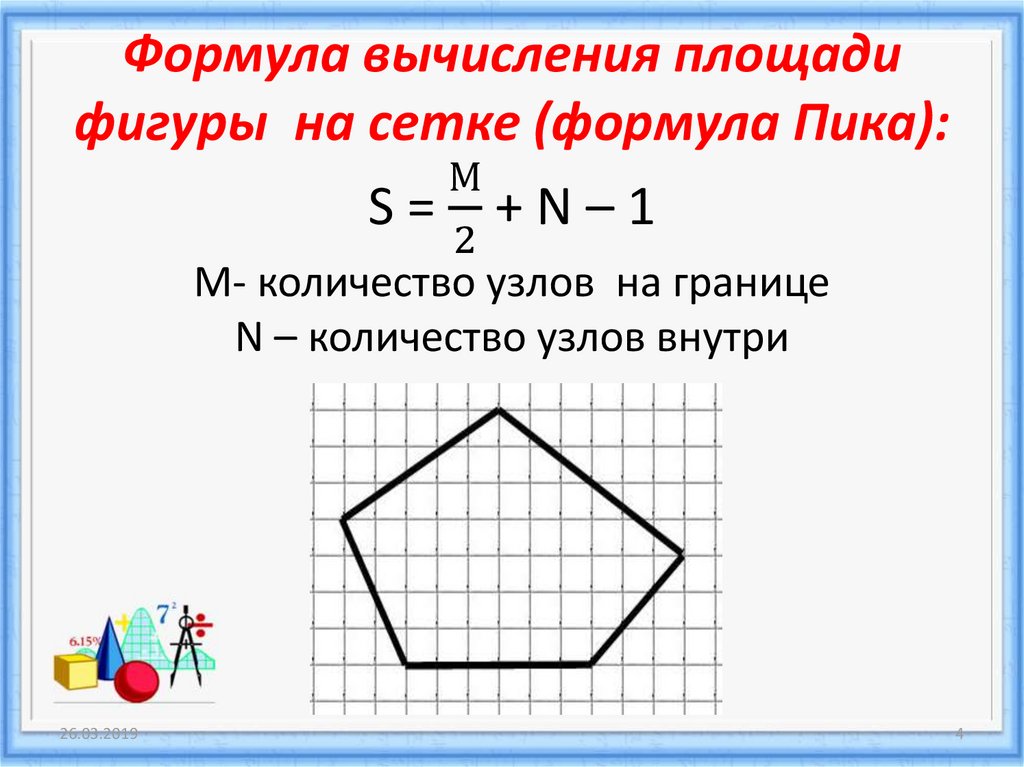
Как быть, если фигура изображена на клетчатой бумаге?
В этой ситуации нужно полагаться на количество клеточек внутри фигуры. По их числу бывает просто посчитать площадь прямоугольника.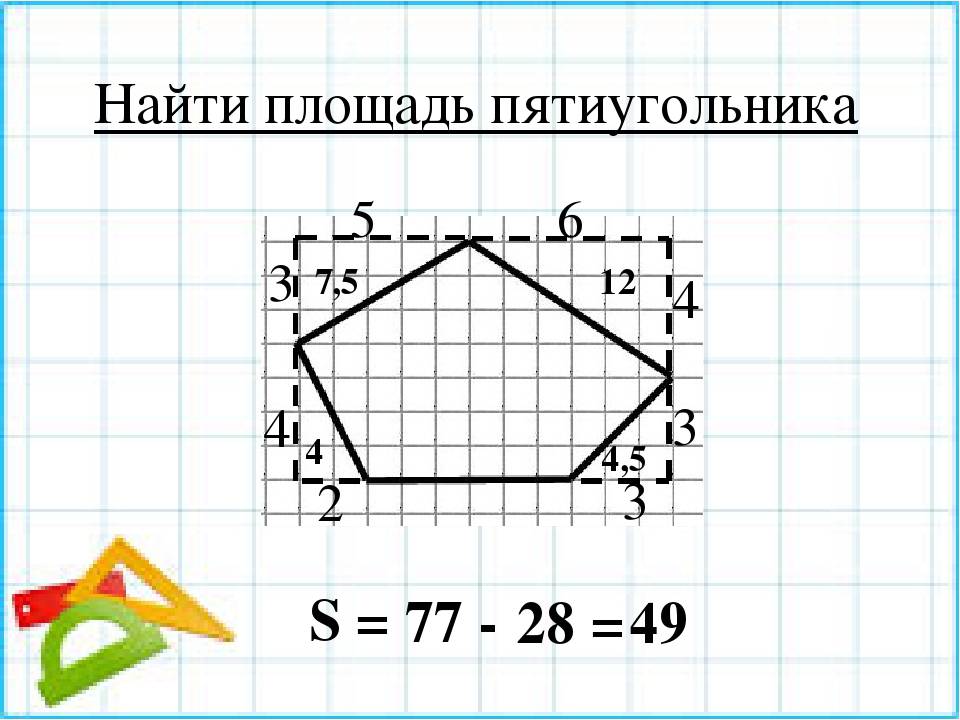 Но это можно сделать тогда, когда стороны прямоугольника совпадают с линиями клеток.
Но это можно сделать тогда, когда стороны прямоугольника совпадают с линиями клеток.
Часто имеет место такое положение прямоугольника, при котором его стороны наклонены по отношению к разлиновке бумаги. Тогда количество клеток определить сложно, поэтому расчет площади прямоугольника усложняется.
Потребуется сначала узнать площадь прямоугольника, который можно прочертить по клеточкам точно вокруг данного. Это просто: перемножить высоту и ширину. Потом вычесть из получившегося значения площади всех А их четыре. К слову, их рассчитывают как половину произведения катетов.
Итоговый результат даст значение площади данного прямоугольника.
Как поступить, если стороны неизвестны, зато даны его диагональ и угол между диагоналями?
До того в этой ситуации нужно вычислить его стороны, чтобы воспользоваться уже знакомой формулой. Поначалу потребуется вспомнить свойство его диагоналей. Они равны и делятся точкой пересечения пополам. Можно увидеть на чертеже, что диагонали делят прямоугольник на четыре равнобедренных треугольника, которые попарно равны друг другу.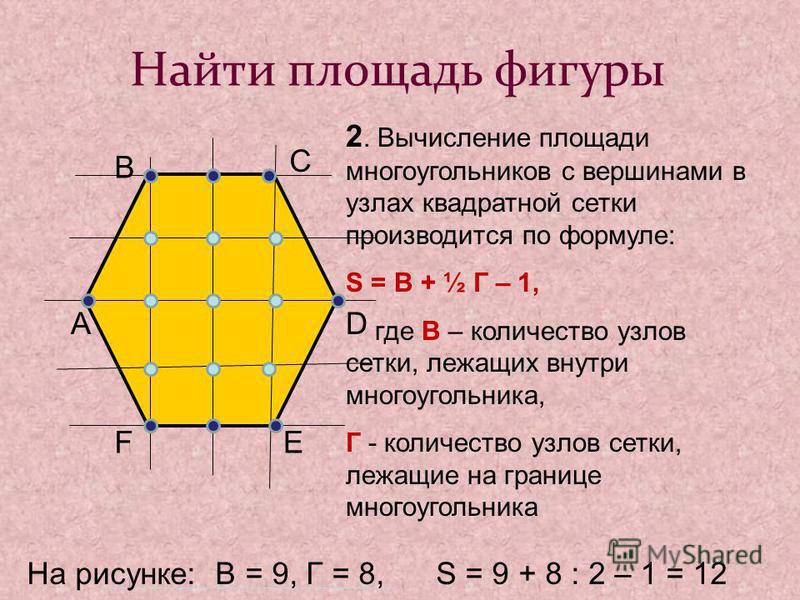
Равные стороны этих треугольников определяются как половины диагонали, которая известна. То есть в каждом треугольнике есть две стороны и угол между ними, которые даны в задаче. Можно воспользоваться
Одна сторона прямоугольника будет вычислена по формуле, в которой фигурируют равные стороны треугольника и косинус заданного угла. Для вычисления второй значение косинуса придется брать от угла, равного разности 180 и известного угла.
Что делать, если в задаче дан периметр?
Обычно в условии указывается еще и соотношение длины и ширины. Вопрос о том, как посчитать площадь прямоугольника, в этом случае проще на конкретном примере.
Допустим, что в задаче периметр некоторого прямоугольника равен 40 см. Известно также, что его длина в полтора раза больше ширины. Необходимо узнать его площадь.
Решение задачи начинается с записи формулы периметра. Его удобнее расписать как сумму длины и ширины, каждую из которых умножить на два по отдельности. Это будет первым уравнением в системе, которую потребуется решить.
Второе связано с известным по условию соотношением сторон. Первая сторона, то есть длина, равна произведению второй (ширины) и числа 1,5. Это равенство нужно подставить в формулу для периметра.
Получится, что он равен сумме двух одночленов. Первый — произведение 2 и неизвестной ширины, второй — произведение чисел 2 и 1,5 и той же ширины. В этом уравнении всего одна неизвестная — это ширина. Нужно ее сосчитать, а потом воспользоваться вторым равенством, чтобы сосчитать длину. Останется только перемножить эти два числа, чтобы узнать площадь прямоугольника.
Расчеты дают такие величины: ширина — 8 см, длина — 12 см, а площадь — 96 см 2 . Последнее число — ответ рассмотренной задачи.
Инструкция
Например, вам , что длина одной из сторон (а) равна 7 см, а периметр прямоугольника (P) равен 20 см. Так как периметр любой фигуры равен сумме длин ее сторон, а у прямоугольника противоположные стороны равны, то его периметр а будет выглядеть следующим образом: P = 2 x (a + b), или P = 2a + 2b. Из этой формулы следует, что найти длину второй стороны (b) можно с помощью несложной операции: b = (P – 2a) : 2. Так, в нашем случае сторона b будет равна (20 – 2 х 7) : 2 = 3 см.
Из этой формулы следует, что найти длину второй стороны (b) можно с помощью несложной операции: b = (P – 2a) : 2. Так, в нашем случае сторона b будет равна (20 – 2 х 7) : 2 = 3 см.
Теперь, зная длины обеих смежных сторон (a и b), вы сможете подставить их в формулу площади S = ab. В данном случае прямоугольника будет равна 7х3 = 21. Обратите на то, что единицами измерения будут уже не , а сантиметры квадратные, так как длин двух сторон единицы их измерения (сантиметры) вы тоже умножали друг на друга.
Источники:
- как находится периметр прямоугольника
Плоская фигура, состоящая из четырех сторон и четырех прямых углов. Из всех фигур площадь прямоугольника приходится вычислять чаще других. Это и площадь квартиры, и площадь садового участка, и площадь поверхности стола или полки. Например, чтобы просто оклеить комнату обоями, вычисляют площадь ее прямоугольных стен.
Инструкция
Кстати, из прямоугольника можно легко вычислить площадь .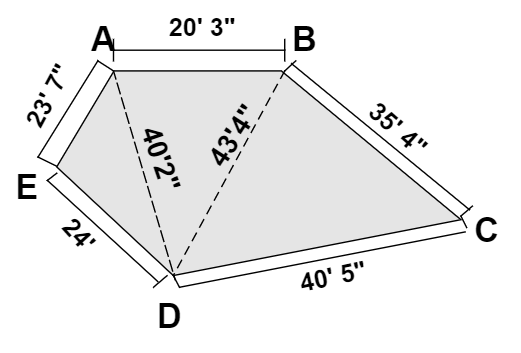 Достаточно достроить прямоугольный до прямоугольника так, чтобы гипотенуза стала диагональю прямоугольника . Тогда будет очевидно, что площадь такого прямоугольника равна произведению катетов треугольника, а площадь
Достаточно достроить прямоугольный до прямоугольника так, чтобы гипотенуза стала диагональю прямоугольника . Тогда будет очевидно, что площадь такого прямоугольника равна произведению катетов треугольника, а площадь
Видео по теме
Частный случай параллелограмма — прямоугольник – известен только в геометрии Евклида. У прямоугольника равны все углы, и каждый из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника , а также из свойств параллелограмма о параллельности противолежащих сторон можно найти стороны фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника основывается на дополнительных построениях и применении свойств получаемых фигур.
Инструкция
Буквой А отметьте точку пересечения диагоналей. Рассмотрите образованный построениями EFА. Согласно свойству прямоугольника его диагонали равны и пополам точкой пересечения А. Вычислите значения FА и EА. Так как треугольник EFА равнобедренным и его
Согласно свойству прямоугольника его диагонали равны и пополам точкой пересечения А. Вычислите значения FА и EА. Так как треугольник EFА равнобедренным и его
Далее вычислите первую EF прямоугольника . Данная сторона является третьей неизвестной стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.
Найдите вторую сторону прямоугольника FG. Для этого рассмотрите другой треугольник EFG. Он является прямоугольным, где известны гипотенуза EG и катет EF. Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.
Относится к простейшим плоским геометрическим фигурам и является одним из частных случаев параллелограмма. Отличительная черта такого параллелограмма — прямые углы во всех четырех вершинах. Ограниченную сторонами прямоугольника площадь можно вычислить несколькими способами, используя размеры его сторон, диагонали и углы между ними, радиус вписанной окружности и т.д.
Отличительная черта такого параллелограмма — прямые углы во всех четырех вершинах. Ограниченную сторонами прямоугольника площадь можно вычислить несколькими способами, используя размеры его сторон, диагонали и углы между ними, радиус вписанной окружности и т.д.
Инструкция
Если известна величина угла (α), который составляет диагональ прямоугольника с одной из его сторон, а также длина (С) этой диагонали, то для вычисления площади можно задействовать определения тригонометрических в прямоугольном . Прямоугольный треугольник здесь образуют две стороны четырехугольника и его диагональ. Из определения косинуса вытекает, что длина одной из сторон будет равна произведению длины диагонали на угла, величина известна. Из определения синуса можно вывести формулу длины другой стороны — она равна произведению длины диагонали на синус все того же угла. Подставьте эти тождества в формулу из предыдущего шага, и получится, что для нахождения площади надо перемножить синус и косинус известного угла, а также длины диагонали 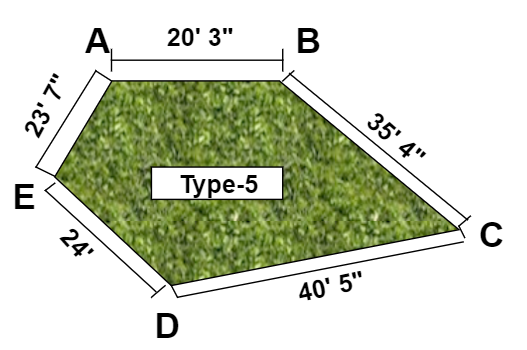
Если кроме длины диагонали (С) прямоугольника известна величина угла (β), который образуют диагонали, то для вычисления площади фигуры можно тоже задействовать одну из тригонометрических функций — синус. Возведите в квадрат длину диагонали и умножьте полученный результат на половину синуса известного угла: S=С²*sin(β)/2.
Если известен (r) вписанной в прямоугольник окружности, то для вычисления площади возведите эту величину во вторую степень и увеличьте результат в четыре раза: S=4*r². Четырехугольник, в который можно , будет являться квадратом, а длина его стороны равна диаметру вписанной окружности, то есть удвоенному радиусу. Формула получена подстановкой длин сторон, выраженных через радиус в тождество из первого шага.
Если известны длины (P) и одной из сторон (A) прямоугольника , то для нахождения площади внутри этого периметра вычислите половину произведения длины стороны на разницу между длиной периметра и двумя длинами этой стороны: S=A*(P-2*A)/2.
Видео по теме
С задачей найти периметр или площадь многоугольника сталкиваются не только ученики на уроках геометрии. Порой ее случается решать и взрослому человеку. Приходилось ли вам рассчитывать необходимое количество обоев для комнаты? Или, может быть, вы измеряли протяженность дачного участка, чтобы огородить его забором? Так знания основ геометрии иногда незаменимы для осуществления важных проектов.
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем жизненном пути встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90°. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в старших классах, приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади прямоугольного треугольника.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать радиус окружности. Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Определение.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника , а короткую — шириной прямоугольника .
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
Диагонали прямоугольника имеют одинаковой длины:
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d 2 = 2a 2 + 2b 2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
| AO = BO = CO = DO = | d | ||
| 2 |
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d 2 — b 2
b = √d 2 — a 2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
| b = d cos | β |
| 2 |
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a 2 + b 2
2. Формула диагонали прямоугольника через площадь и любую сторону:
Формула диагонали прямоугольника через площадь и любую сторону:
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = D о
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S: sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b )
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a 2 | = | 2S + 2b 2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d 2 — a 2 ) = 2(b + √d 2 — b 2 )
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R 2 — a 2 ) = 2(b + √4R 2 — b 2 )
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √D o 2 — a 2 ) = 2(b + √D o 2 — b 2 )
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a √4R 2 — a 2 = b √4R 2 — b 2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a √D o 2 — a 2 = b √D o 2 — b 2
Окружность описанная вокруг прямоугольника
Определение.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
- Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников.
 Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
- Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.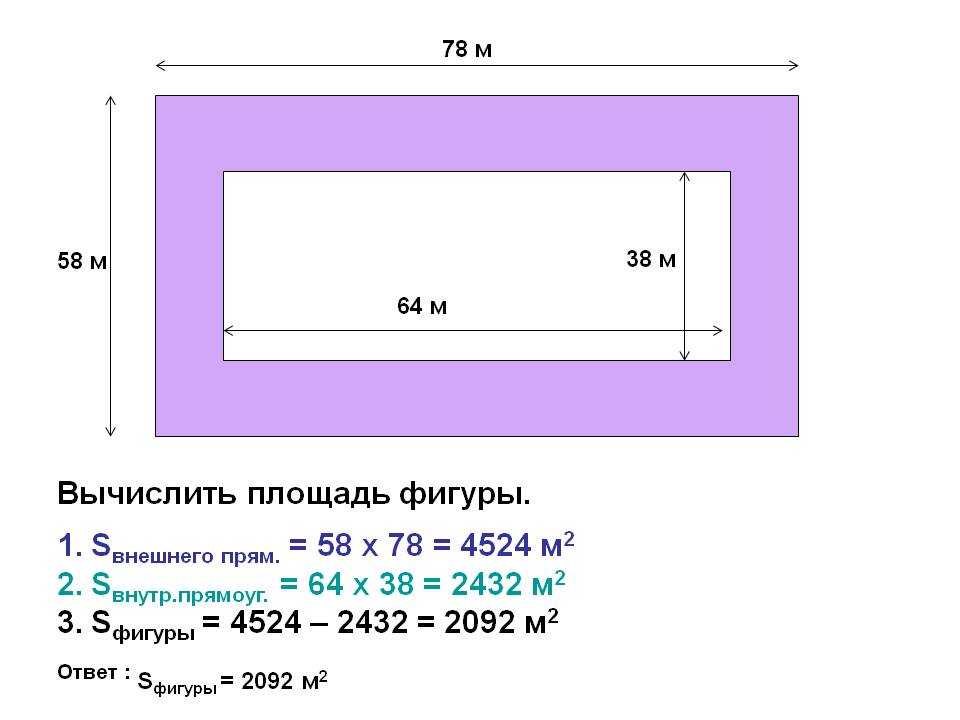
- Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Как рассчитать площадь в квадратных футах
Как рассчитать площадь в футах
Площадь в футах — это измерение площади, покрывающей площадь. Его часто используют для определения площади пола в доме. Знание квадратных метров также пригодится при покраске, укладке плитки и ландшафтных проектах. Чтобы найти квадратные метры комнаты, нужно вычислить площадь. В зависимости от формы комнаты найти площадь может быть так же просто, как умножить два измерения. Это может также включать немного более сложную математику. Например, вы можете рассчитать квадратные метры прямоугольной комнаты, умножив ее длину и ширину (ДхШ). Напротив, для расчета квадратных метров круглой комнаты вам понадобится другая формула (A=πr2).
Его часто используют для определения площади пола в доме. Знание квадратных метров также пригодится при покраске, укладке плитки и ландшафтных проектах. Чтобы найти квадратные метры комнаты, нужно вычислить площадь. В зависимости от формы комнаты найти площадь может быть так же просто, как умножить два измерения. Это может также включать немного более сложную математику. Например, вы можете рассчитать квадратные метры прямоугольной комнаты, умножив ее длину и ширину (ДхШ). Напротив, для расчета квадратных метров круглой комнаты вам понадобится другая формула (A=πr2).
Важное примечание. Прежде чем вычислять квадратные футы любой проблемы, очень важно сначала преобразовать измеренные размеры в футы (если они уже не в футах). Преобразование измерений можно выполнить с помощью нескольких простых правил:
Чтобы преобразовать метры в футы, умножьте число на 3,281 (например, 10 м = 32,81 фута)
Чтобы преобразовать ярды в футы, умножьте число на 3 (например, 12 ярдов = 36 футов)
Чтобы перевести дюймы в футы, разделите число на 12 (например, 12 дюймов = 1 фут)
Чтобы преобразовать сантиметры в футы, умножьте число на 0,03281 (например, 1000 см = 32,81 фута)
прямоугольную или квадратную область легко.
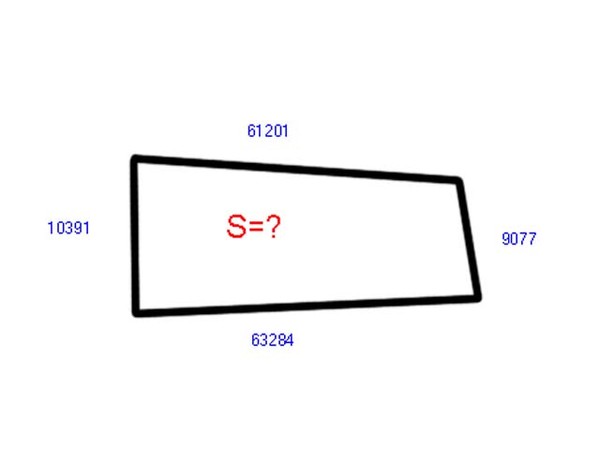 Все, что нужно, это несколько быстрых шагов.
Все, что нужно, это несколько быстрых шагов.Измерение длины комнаты
Измерение ширины комнаты
Преобразование линейных единиц в футы (при необходимости)
Вычислите площадь, перемножив две цифры, чтобы получить результат.
Квадратные футы = Д x Ш
Где:
Д = длина
Ш = ширина
Пример
Сколько квадратных метров занимает прямоугольная комната размером 4 на 3 м?
Квадратные футы = Д x Ш
Во-первых, нам нужно преобразовать измерения в футы.
Чтобы преобразовать метры в футы, умножьте число на 3,28
4 x 3,281 = 9
3 x 3,281 = 13,121 фута
Квадратный фут = 129,15 кв. фута (9,843 x 13,121)
фута (9,843 x 13,121)
Как рассчитать квадратные футы для треугольной площади решить для его площади. Наиболее распространенный подход к вычислению площади треугольника состоит в том, чтобы умножить половину длины его основания на его высоту (расстояние от основания до высшей точки треугольника).
Это суммируется формулой = 1/2bh (1/2 x b x h).
Где
b = длина основания в футах
h = высота в футах
Пример:
Найдите площадь треугольника высотой 4 фута с основанием 10 футов.
Используйте формулу 1/2bh (1/2 x b x h).
Если основание треугольника равно 10 футам, а его высота равна 4 футам, его общая площадь будет равна:
½ x 10 x 4 = 20
Площадь = 20 кв. футов
Как рассчитать квадратные футы для треугольника Площадь с использованием длин сторон
Если основание и высота треугольника неизвестны, вы можете рассчитать площадь треугольного пространства, используя длину трех его сторон. Это делается с помощью формулы Герона, которая гласит:
Это делается с помощью формулы Герона, которая гласит:
Площадь = √s(s-a) (s-b) (s-c)
Где
a, b и c = длина стороны треугольника
s = полупериметр треугольника
Пример
Найдите площадь треугольной комнаты со сторонами 11 футов, 15 футов и 14 футов
Площадь = √s(s-a) (s-b) (s-c)
s = Периметр/2
Периметр = 11 + 15 + 14 =40
S = 40/2 = 20
Площадь = √0 20-11) (20-15) (20-14)
Площадь= √20(9)(5)(6)
Площадь= 73,4847 кв. футов
Как рассчитать квадратные футы для круга
Рассчитайте квадратные метры круга, используя формулу: A=πr2
Где A = площадь круга
Π = 3,14159
r = радиус (Совет: чтобы найти радиус комнаты, просто разделите диаметр на два ).
Пример:
Рассчитайте площадь круглой комнаты диаметром 12 футов.
Чтобы решить задачу:
Сначала вычислите радиус, который равен половине диаметра. 12/2 = 6 футов.
Далее решайте область с использованием a = πr2, где π = 3,1415
3,1415 x (6) 2 = 3,1415 x 36
Область = 113,094 кв. Форма
Чтобы вычислить площадь неправильной формы, разделите неправильную форму на меньшие фигуры, найдите площадь каждой из них, а затем сложите все результаты.
Пример:
Найдите площадь неправильной фигуры ниже.
Чтобы найти площадь в квадратных футах, разделите неправильную форму на несколько квадратов или прямоугольников, обозначенных A, B, C и D.
Найдите площадь A, B, C и D.
Общий квадратный фут = площадь A + площадь B + площадь C + площадь D
Как расчет квадратных футов используется в реальной жизни?
Квадратные метры используются во многих профессиях, включая некоторые из самых популярных шестизначных профессий. Например, инженеры-программисты или юристы, желающие расшириться, будут полагаться на квадратные метры при покупке нового офиса. Точно так же менеджеры по строительству, которые наблюдают за реализацией новых проектов, используют цифры в квадратных футах, чтобы убедиться, что у них достаточно материалов для завершения проекта, над которым они работают.
Например, инженеры-программисты или юристы, желающие расшириться, будут полагаться на квадратные метры при покупке нового офиса. Точно так же менеджеры по строительству, которые наблюдают за реализацией новых проектов, используют цифры в квадратных футах, чтобы убедиться, что у них достаточно материалов для завершения проекта, над которым они работают.
Площадь параллелограмма ИЛИ площадь неправильных форм – площадь в квадратных футах
Площадь параллелограмма ИЛИ площадь неправильных форм (squarefootagearea.com) Квадратные футы = Квадратные футы = Кв. футы = Кв. футы = кв. футы = футы 2
База ( б ):
Высота ( ч ):
Сторона а*:
Сторона b*:
Сторона с*:
Сторона d*:
Сумма 2 углов*:
Помните, что ввод может быть только в футах (футах), дюймах (дюймах), ярдах (ярдах), сантиметрах (см), миллиметрах (мм) и метрах (м), но никогда не используйте комбинацию двух разных единиц!. . Если у вас есть входы в разных единицах измерения. Пожалуйста, обратитесь к нашей таблице преобразования ниже.
. Если у вас есть входы в разных единицах измерения. Пожалуйста, обратитесь к нашей таблице преобразования ниже.
Формула
Площадь = b × h
Какая разница между правильной и неправильной формой?
Правильная форма: Все стороны и углы правильных фигур равны.
Неправильная форма: Стороны и углы неправильной формы могут быть любой длины и размера.
Правильная форма
Неправильная форма
Как вычислить площадь неправильной формы?
Теперь, когда мы знаем разницу между правильными и неправильными формами. Давайте упростим наш процесс расчета, разделив неправильную форму на правильные формы. Посмотрите пример ниже, здесь мы разделили фигуры на треугольники, которые имеют правильную форму.
Затем вы можете легко вычислить площадь каждого треугольника с помощью формулы Герона.
После вычисления площади каждого треугольника просто сложите их все, чтобы найти площадь неправильной формы.
Как пользоваться калькулятором нестандартных площадей?
Шаг 1: Измерьте все стороны площади в одной единице (футы, метры, дюймы или любые другие).
Шаг 2: Введите длину горизонтальных сторон в поля «Длина 1» и «Длина 2». И ширину вертикальных сторон в поля «Ширина 1» и «Ширина 2». (См. изображение выше).
Шаг 3: Нажмите кнопку расчета. Вывод, который дает наш калькулятор, не зависит от единицы измерения. Например, если вы ввели значения в футах. Вывод всегда будет в футах.
Наша формула: Площадь = B × H
Сокращения. См 2 = Квадратные сантиметры
Мм 2 = Квадратные миллиметры
M 2 = Квадратные метры
Шаг 1: Определите все стороны неправильной формы. Убедитесь, что все стороны имеют одинаковую форму.
Шаг 2: Нарисуйте площадь на листе бумаги, используя полученные измерения. Помните, что ваш рисунок должен быть в масштабе.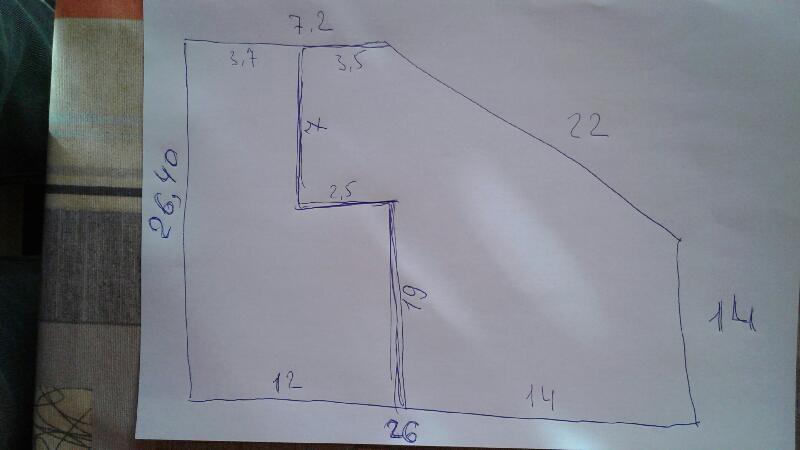

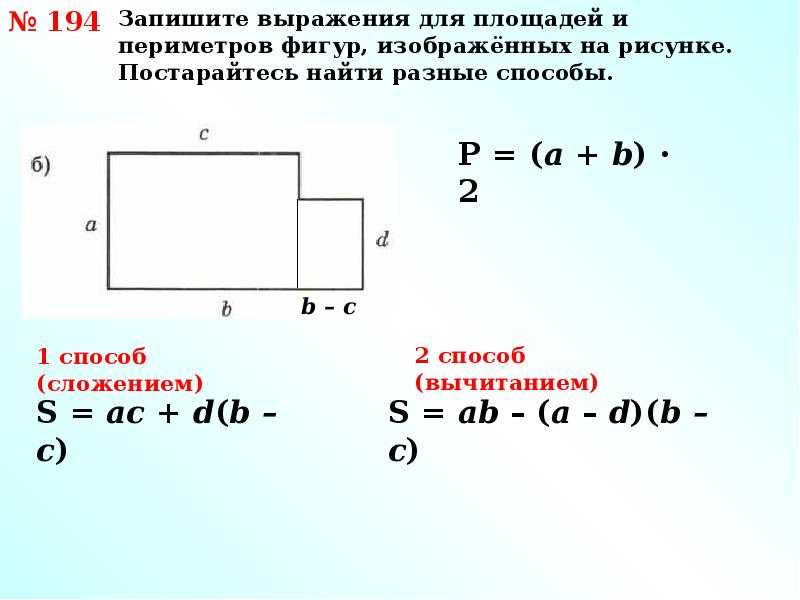 Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.