Шаг арматуры: Армирование ленточного фундамента — статьи СК «ДОМАПЕРМЬ.РФ»

Правила армирования

Правила армирования

Для продольного и поперечного армирования ленточного фундамента используется арматура класса A-III (A400) или А500. Для вспомогательного поперечного армирования (изготовления хомутов), помимо А400 и А500, может использоваться стержневая горячекатаная гладкая арматура класса A-I (А240), А-II, проволока (гладкая арматура) класса Вр-I. Продольные рабочие стрежни арматуры ленточного фундамента воспринимают совместно с бетоном основные нагрузки растяжения и сжатия, действующие вдоль продольной оси фундамента.  

   Кроме продольных стержней при армировании лент фундамент может устанавливаться поперечная арматура (хомуты) из расчета на восприятие нагрузок, действующих вдоль поперечной оси фундамента. Хомуты устанавливаются в ленту при её высоте более 15см.  Также поперечная арматура служит для ограничения развития трещин в бетоне, для удержания продольных стержней в проектном положении, и для закрепления от их бокового выпучивания при воздействии сжимающих нагрузок.

В случае сжимающих нагрузок хомуты  следует устанавливать с шагом не более 15 диаметров сжатой продольной арматуры и не более 50 см, а конструкция хомутов должна обеспесивать отсутствие выпучивания продольной арматуры в любом направлении. Поперечная арматура устанавливается у всех поверхностей фундамента, вблизи которых устанавливается продольная арматура. Закрепление поперечной арматуры производят путем ее загиба и охвата продольной рабочей арматуры. 
 Также в фундаменте может использоваться конструктивная арматура, устанавливаемая  для восприятия непредусмотренных усилий, таких как усилия от усадки бетона или температурных деформаций. В частности, для фундаментных лент высотой сечения более 70 см рекомендуется установка дополнительной продольной  конструктивной арматуры на каждые  40 см  высоты ленты. По возможности арматуру следует монтировать укрупненными или пространственными заранее изготовленными элементами, по возможности сокращая объем применения отдельных стержней.

Процент армирования

   Существует некий допустимый диапазон армирования, определённый Сводом Норм и Правил (Пункт 7. 3.5 СНиП 52-01-2003 «Бетонные и железобетонные конструкции»), который является одним из определяющих факторов выбора пространственной схемы армирования и может повлиять на выбор сечения ленты фундамента. Этот параметр лежит в диапазоне от 0,3 до 3% для балок, и не менее 0,1% для фундаментов. При армировании ленточных фундаментов, служащих опорой под колонны (например, при строительстве монолитного железобетонного каркаса здания) площадь сечения продольной арматуры для ребра Т-образного ленточного фундамента предусматривают с процентом армирования не менее 0,4% в каждом ряду. Это относительное содержание продольной рабочей арматуры в бетонном элементе от площади рабочего сечения этого элемента. Например, если у вас лента сечением 300х400мм, то площадь S сечения 300*400=120 000 мм.кв. Минимальное сечение арматуры составит 120 мм.кв., или 4 прута арматуры диаметром 8 мм (или 2 прута диаметром 10мм). Максимум можно заложить 10 прутов диаметром 22мм! Меньшее количество арматуры незначительно укрепит бетон и практически будет равно просто силе бетона на разрыв, но и больше 3% арматуры тоже не хорошо — арматуры будет столько, что она не успеет включится в работу, как бетон уже будет разрушен возникшей нагрузкой. Если расчёт приведёт вас к проценту армирования более 3%, нужно задуматься над увеличением сечения бетонного элемента. Сечение арматуры нетрудно посчитать, но для облегчения и визуализации я составил табличку сечений при разных количествах прутов арматуры:

Еще один пример из расчёта своего ростверка: У меня было рассчитано сечение ленты-ростверка как 22х30см, Это 66000 мм.кв. Расчёт армирования привёл меня к 6 прутам арматуры диаметром 12мм (3 снизу и 3 сверху) — это 678 мм.кв. арматуры. Посчитаем процент армирования: 678*100/66000=1,027% — он вписывается в допустимый диапазон от 0,1% до 3%, а значит выбранное соотношение между сечением бетона и армированием находится в «равновесии», количество арматуры и бетона экономически и расчётно обосновано. Подошло бы и 5 прутов по 12мм (565*100/66000=0,856%), расчёт по нагрузкам давал 45% запаса по прочности, однако я решил немного перестраховаться заложив 6-й прут и получил 90% запаса.

Диаметр арматуры

   Помимо минимального процента армирования существуют и требования по минимальному диаметру арматуры. Например, для продольной рабочей арматуры нельзя использовать арматуру диаметром менее 10мм. Продольную рабочую арматуру рекомендуется назначать из стержней одинакового диаметра. Если же применяются стержни разных диаметров, то стержни большего диаметра следует размещать внизу ленты фундамента,  в углах сечения ленты фундамента и в местах перегиба хомутов через рабочую арматуру. Стержни продольной рабочей арматуры должны размещаться равномерно по ширине сечения ленты фундамента. При этом размещение стержней арматуры верхнего ряда над просветами между арматурой нижнего ряда запрещается [пункт 3.94 Руководства по конструированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения, Москва, 1978]. При этом как в сварных, так и в вязаных каркасах диаметр продольных стержней должен быть не менее диаметра поперечных стержней арматуры. Максимальный диаметр сжатых стержней (для верхнего ряда) вряд-ли будет достигнут частными домостроителями, но для справки, он не должен быть более 40мм. Для удобства я собрал эти требования в нижеследующей табличке:

Минимальное количество стрежней продольной рабочей арматуры в одном ряду

     В балках и ребрах шириной более 15 см число продольных рабочих растянутых стержней в поперечном сечении должно быть не менее двух. При ширине элемента 15 см и менее допускается устанавливать в поперечном сечении один продольный стержень. При этом устройство ленточных фундаментов шириной менее 15 см не допускается.

Максимальное количество стержней продольной арматуры в одном ряду и минимальное расстояние между стержнями арматуры

   Максимальное количество стержней в одном ряду в поперечном сечении монолитной бетонной балки определяется минимальным расстоянием в свету между отдельными стержнями продольной арматуры. Это минимальное  расстояние определено необходимостью свободного протекания бетонной смеси в тело ленты между стержнями арматуры фундамента при заливке бетона, возможностью его уплотнения и хорошей связи бетона с арматурой для совместной работы под нагрузкой.  Минимальные расстояния между стрежнями продольной арматуры определены в пункте 7.3.4 СНиП 52-01-2003  “Бетонные и железобетонные конструкции”. Минимальное расстояние между стержнями продольной арматуры не может быть меньше наибольшего диаметра стержней арматуры и не менее 25 мм для нижнего ряда арматуры и 30 мм — для арматуры верхнего ряда при двух рядах армирования. При трех рядах армирования расстояние между стрежнями арматуры в верхнем ряду должно составить не менее 50 мм. При большом насыщении арматурой должны быть предусмотрены отдельные места с расстоянием между стержнями арматуры в 60 мм для прохождения между арматурными стержнями наконечников глубинных вибраторов, уплотняющих бетонную смесь. Расстояния между такими местами должны быть не более 500мм. Например, имеем ленту фундамента сечением 40х30см с двумя рядами арматуры. Создаются следующие ограничения: 1 — защитный слой бетона по 40мм с каждой стороны; 2 — минимальный диаметр арматуры 10мм; 3 — минимальное расстояние между арматурой 30мм. Итого, соблюдая все ограничения, получается возможным разместить по 6 рядов арматуры, при этом в верхнем ряду нужно один прут исключить для прохождения наконечника вибратора. Допустим, если бы высота ленты была 100 см, то возникает необходимость использовать три ряда арматуры, а это увеличивает минимальное расстояние между арматурой до 50 мм. В этом случае в одном ряду умещается не более 4 прутов арматуры.

Количество рядов арматуры

   В обычных условиях для индивидуальных домов в фундаменте достаточно двух рядов арматуры. Нижний, в большей степени работающий на растяжение и верхний, работающий на сжатие, если не возникнут выталкивающие силы грунтов. При высоте ленты до 70 см средних рядов арматуры делать не нужно, т.к. она там не работает, там не возникает ни растяжений, ни сжатий (если только не аварийная ситуация). Дополнительное  продольное армирование может понадобиться, если высота фундаментной ленты превышает 70 см. В этом случае лента фундамента рассматривается как балка, которой требуется конструктивное армирование. Стержни арматуры при конструктивном армировании не у граней балки (в середине ширины балки) не требуются. Они должны ставиться тлько у боковых поверхностей балок высотой поперечного сечения более 70 см. Расстояние между конструктивными стрежнями арматуры по высоте должно быть не более 40 см.

    Площадь сечения таких арматурных стрежней определяется не менее 0,1 % площади сечения бетона, но не от всей площади сечения балки, а от площади, образуемой расстоянием между этими стержнями и половиной ширины балки, но не менее чем 20 см. Например, при расстоянии между рядами арматуры по вертикали в 40 см и ширине ленты 30 см, определяемая минимальная площадь сечения арматуры будет отсчитываться от площади в 400 мм x 300 мм /2 =60 000 мм2 х 0,001=60 мм2 . Эти арматурные стержни должны соединяться хомутами или шпильками диаметром 6 — 8 мм из арматуры класса A-I с шагом 50 см по длине ленты фундамента.

Максимальный шаг между продольными стержнями арматуры

Максимальный шаг установки поперечной арматуры

Толщина бетонного защитного слоя арматуры

   Защитный слой бетона, то есть расстояние от поверхности арматуры до соответствующей грани фундаментной ленты, предназначен для обеспечения совместной работы арматуры с бетоном, для закрепления (анкеровки) арматуры в бетоне и возможности устройства соединения арматуры. Также защитный слой бетона предохраняет арматуру от воздействия факторов окружающей среды, конструкций, в том числе и от огня.  Толщина защитного слоя бетона зависит от типа конструкции и роли арматуры в ней, ее диаметра и условий окружающей среды.

   Для продольной рабочей арматуры толщина защитного слоя должна быть, как правило, не менее диаметра стержня и не менее: 30 мм — для фундаментных балок и сборных фундаментов; 35 мм — для монолитных фундаментов при наличии бетонной подготовки; 70 мм — для монолитных фундаментов при отсутствии бетонной подготовки. При использовании бетонной подготовки (или на скальном грунте) – толщина бетонного защитного слоя снижается в отечественных нормах до 40 мм, а в американских до 25мм. Для сборных элементов минимальные значения толщины защитного слоя бетона рабочей арматуры уменьшают на 5 мм. Для конструктивной арматуры минимальные значения толщины защитного слоя бетона принимают на 5 мм меньше по сравнению с требуемыми для рабочей арматуры. Во всех случаях толщину защитного слоя бетона следует также принимать не менее диаметра стержня арматуры.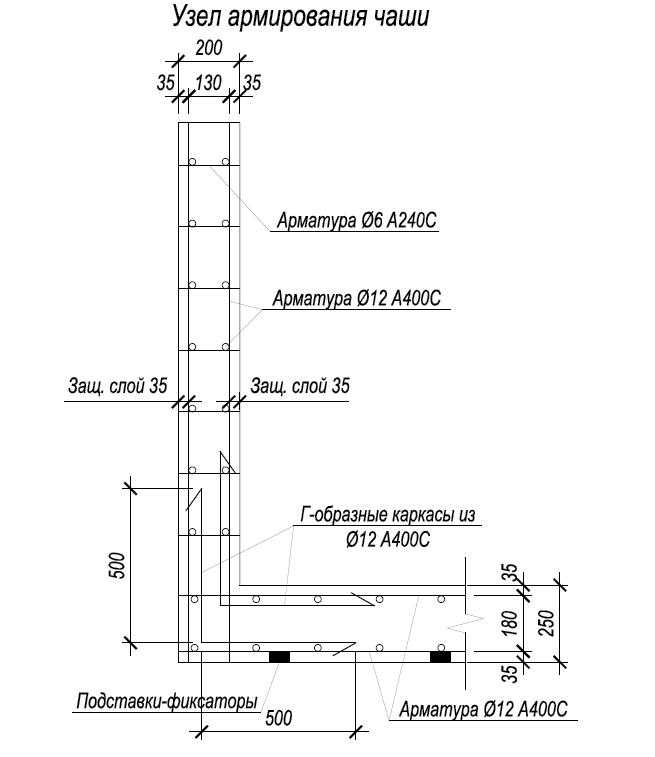

    По требованиям ACI 318-05  защитный слой бетона на уличную строну для арматуры до 20 мм составляет 25 — 40 мм. Для диаметра арматуры толще 20 мм — 50 мм. Защитный слой для арматуры диаметром до 40 мм на стороне не подверженной действию природных факторов составляет 20 мм. По отечественным нормам защитный слой бетона с обеих сторон составляет 40 мм. Требуемую величину защитного слоя нижней арматуры и проектное положение арматуры в процессе бетонирования можно установить с помощью пластиковых фиксаторов, подкладок из бетона и  путем конструирования арматурного каркаса таким образом, чтобы некоторые стержни упирались в опалубку, фиксируя положение каркаса. Нижний защитный слой можно установить, закладывая под нижние стержни арматуры заранее изготовленные бетонные прокладки (сухари) размером 100×100 мм и толщиной, равной требуемой толщине защитного слоя. Применение прокладок из обрезков арматуры, деревянных брусков и щебня запрещается. Также для задания толщины защитного можно использовать пластиковые фиксаторы — спейсеры требуемого стандартного размера. Фиксаторы для арматуры выпускаются в размерах от 15 до 50 мм с шагом размера 5 мм.
Толщина защитного слоя для поперечной арматуры бетонных элементов сечением меньше 25 см составляет 1 см, а для элементов сечением более 25 см – 1,5 см.

Требования к поверхности арматуры

    Арматуру следует монтировать укрупненными или пространственными заранее изготовленными элементами, по возможности сокращая объем применения отдельных стержней. С бетонной подготовки (подушки) в местах установки арматуры должны быть удалены мусор, грязь, снег и лед. Стержни арматуры должны быть обезжирены, очищены от любого неметаллического покрытия, краски, грязи, льда и снега, отслаивающегося налета ржавчины. Удаляется отслаивающаяся ржавчина с помощью металлической щетки. Разрешается наличие эпоксидного покрытия на арматуре. Существует мнение некоторых строителей — поливать водой арматуру за несколько дней перед укладкой, чтобы она заржавела и к ней сильнее прилипал бетон. В официальных комментариях к нормам указано: Обычная поверхностная неотслаивающаяся ржавчина усиливает силу сцепления арматуры с бетоном.  Ржавая поверхность лучше склеивается с цементным гелем в составе бетона. Но отслаивающуюся ржавчину требуется удалить. Арматура периодического профиля имеет в 2-3 раза большее сопротивление выдергиванию, чем гладкая арматура. А арматура с гладкой полированной поверхностью держится в бетоне еще в 5 раз слабее.

Сварка или вязка арматуры

    Идеальным армированием фундамента является армирование сплошным безразрывным контуром арматуры. Однако, такое безразрывное армирование может быть получено только с использованием сварки или с использованием специальных резьбовых соединителей. В строительстве фундаментов часто применяют арматуру класса А-III А400 — такую арматуру сваривать недопустимо, она сильно теряет в прочности при нагревании. Сваривать можно только арматуру c литерой «С» в маркировке, например А500С.  Длина сварного шва для такой арматуры должна быть не менее 10 диаметров. Т.е. если арматура диаметром 12мм, то шов должен быть не менее 120мм. При этом отечественные нормы разрешают дуговую электросварку перекрестий арматуры только не менее 25 мм диаметром.

   Соединение арматуры нахлестом – самый распространенный вариант в дачном строительстве  из-за своей очевидной простоты исполнения. Однако есть ряд требований, которые необходимо выполнить, чтобы обеспечить правильную работу соединяемой арматуры. Соединение арматуры нахлестом допустимо для арматуры диаметром до 36 мм. Это ограничение связано с отсутствием экспериментальных данных по соединениям нахлестом для арматуры больших диаметров. Соединение арматуры не должно размещаться в местах концентрированного приложения нагрузки и местах наибольшего напряжения. Соединение арматуры нахлестом может производиться:

• Со связкой стержней вязальной проволокой. В этом случае расстояние между прутами обусловлено лишь высотой выступов периодического профиля и может приниматься равным нулю.

• Без связки. В случае свободного соединения с нахлестом расстояние между стыкуемыми нахлестом стержнями арматуры по вертикали и горизонтали должно быть не менее 25 мм или 1 диаметр арматуры, если диаметр арматуры больше 25 мм,  для обеспечения свободного проникновения бетона.

  Максимальное расстояние по ширине ленты фундамента между стыкуемыми свободным нахлестом стержнями должно быть не более 8 диаметров стержней арматуры. В нормативах ACI 318-05 рекомендуется делать свободные (не связанные) соединения стержней арматуры  в предварительно не напряженных конструкциях. Это объясняется тем, что при свободном соединении бетон охватывает все стороны каждого арматурного стержня и фиксирует стержень арматуры надежнее, чем при обхвате неполной окружности стержня при связке его проволокой с соседним стержнем.

• Механическим способом.  C точки зрения экономии (перерасход арматуры на нахлесты до 27%), и безопасности здания (ограничение объема бетона в месте стыков), арматуру диаметром свыше 25 мм рекомендуется соединять механическим способом (винтовые муфты или опрессованые соединения).

  Соседние соединения арматуры по длине должны быть разнесены в разбежку так, чтобы в одном сечении одновременно соединялось не более 50% арматуры. минимальное расстояние между стыками арматуры по длине составляет 61 см. Не более половины всех стержней в одном расчетном сечении элемента фундаментной ленты могут иметь соединения. Стыкование отдельных стержней арматуры и сварных сеток без разбежки допускается при использовании арматуры для конструктивного (нерабочего) армирования.

  Нормы для анкеровки арматуры, работающей как на растяжение, так и на сжатие предусматривают нахлест стержней в 50 диаметров этих стержней, но не менее 30 см. Однако, величина нахлеста зависит и от класса (марки бетона: если для бетона класса В15 (M200) минимальный нахлест составляет  50d (диаметров арматуры), то при использовании бетона класса  В20 (M250), нахлест можно уменьшить до 40d. Для бетона класса В25 (M300) минимальный нахлест равен 35d. Для арматуры А-I и А-II минимальный нахлест равен 40d.

В общем, в двух словах: 1 — арматуру лучше вязать, чем варить, 2 — нахлёсты лучше не связывать, а оставлять между прутами расстояние около 25мм.

Наблюдения

  Только соблюдая все эти ограничения и рекомендации можно сказать, что вы получите достаточное для большинства случаев армирование без дополнительных расчётов! Жизненные наблюдения показывают, что обычно люди льют столько бетона в фундамены, что если бы они их так же основательно армировали, то можно было бы на их фундаментах строить многоэтажки (правда, несущая способность грунтов обычно никак не учитывается). В большинстве случаев застройщики стремятся к самому минимальному проценту армирования, поскольку бетона у них такое количество, что даже 0,1% арматуры выглядит внушительно.  

Основные нарушения правил армирования

•   Некоторые строители армируют углы ленточных фундаментов и примыканий лент с помощью перекрестий стрежневой арматуры. Такой способ является грубейшим нарушением типовых схем армирования углов и примыканий, ослабляющих конструкцию, который может привести к расслоению бетона. Не смотря на именно такую рекомендацию автора технологии ТИСЭ Яковлева я считаю это совершенно неприемлемым способом.

•    Арматуру класса А-III можно гнуть в холодном состоянии на угол до 90° по диаметру изгиба с оправкой радиусом равным пяти диаметром сгибаемой арматуры без потери прочности. При загибе арматуры на 180 градусов прочность арматуры снижается на 10%. По американским нормам диаметр оправки  для арматуры номинальным диаметром до 26 мм сгибается по диаметру равному шести диаметрам сгибаемой арматуры, а арматура диаметром 28-36 мм сгибается по восьмикратному диаметру.

  При этом свободный загибаемый конец арматуры должен быть не короче 12 диаметров стержня арматуры. Нельзя сгибать арматуру, один конец которой уже замоноличен в бетон.  

•    Практикуется как минимум два широко распространенных недопустимых приема гибки арматуры.  Если заказчик требует от рабочих сгибать арматуру для армирования углов и примыканий фундаментной ленты (как и положено), а не класть ее перекрестиями, то рабочие, ленясь, либо нагревают место сгиба автогеном, на костре или паяльной лампой, либо надпиливают место сгиба арматуры болгаркой. Понятно, что оба способа значительно ослабляют стрежни арматуры, что может привести к разрушению их целостности под  нагрузкой. Требование (пункт 7.3.1 ACI 318-08) гласит: Все виды арматуры должны сгибаться в холодном состоянии, если иное не предписано проектировщиком.

• Некоторые строители считают, что в качестве рабочей арматуры можно использовать любой металл любой конфигурации: трубы, алюминиевые изделия, плоские листы, отходы от промышленной вырубки деталей, сетку рабицу, проволоку и т. п. Все эти материалы не обладают требуемыми характеристиками, чтобы адекватно воспринять нагрузки на сжатие или растяжение, и не предохраняют бетон от деформаций и образования трещин. Армирование рельсами также не рекомендуется из-за низкого сцепления бетона с гладкой поверхностью металла.  Включение в состав бетона алюминия приводит к химическим реакциям, разрушающим бетон. 

Как выбрать и рассчитать арматуру для фундамента, Расчет арматуры для фундамента

4 июня 2021 г.

Фундамент — строительная конструкция, воспринимающая нагрузку от находящегося над ним сооружения и распределяющая ее по всему основанию.

При строительстве зданий применяются следующие виды фундаментов:

• ленточные;
• столбчатые;
• свайные;
• плитные;
• комбинированные.

Выбор конкретного типа фундамента зависит от вида залегающих в его основании грунтов, специфики возводимого здания и формируемой им нагрузки, сейсмической активности в регионе строительства.

Фундамент закладываются ниже глубины промерзания грунта, чтобы предотвратить разрушение, как самого фундамента, так и всего строения в следствии промерзания и оттаивания грунта.

Фундаменты испытывают нагрузки связанные с весом здания, сдвигом грунта и морозного пучения. При этом разные части фундамента одновременно подвергаются и сжатию, и растяжению.

На фундамент действуют следующие виды нагрузки:

• на сжатие – под весом строения;
• на разрыв – пучение грунта действует зимой, неравномерно сжимает стенки и пытается поднять вверх;
• на излом / сдвиг — горизонтальные подвижки грунта при замерзании действуют зимой, а сдвиг водонасыщенных или слабых грунтов действует летом.

Бетон не пластичный материал и при растяжении и кручении разрушается.

Для того чтобы предотвратить появление трещин в фундаменте его необходимо армировать.

Армирование позволяет распределить нагрузку по всей конструкции фундамента, позволяет избежать появления трещин и изломов, увеличить его жесткость, устойчивость к перепадам температур, силам растяжения, кручения и сжатия.

Армирование фундамента — предназначено для укрепления бетона, материалом, обладающим более высокими свойствами по прочности.

Для повышения прочности (армирования) фундамента используется строительная рифленая стальная или композитная арматура.

Строительная арматура — это стержни заданного диаметра из металла или композитных материалов, с гладкой или рифленой поверхностью, монтируемые в железобетонные конструкции и предназначенные для восприятия, распределения и компенсации нагрузок на растяжение и изгиб.

Для разных типов фундаментов используются соответствующие схемы монтажа арматуры, в результате формируются так называемые арматурные каркасы и арматурные сетки.

Согласно принятым в сфере строительства методиками классификации арматуры, см. статью «Сортамент арматуры», арматурный прокат (арматуру) принято подразделять на:

По наличию рифелей (профиля) на поверхности прутков на:

• гладкую или арматура А1;
• рифленую или арматура А3 / А4 / А5 / А6.

По применению, в процессе армирования на:

• рабочую арматуру — предназначенную для компенсации нагрузки в готовых железобетонных изделиях;
• конструктивную или распределительную арматуру — предназначенную для компенсации усадки / расширения, темперных воздействий;
• монтажную арматуру — предназначенную для соединения рабочей и конструктивной;
• анкерную арматуру — используется при изготовлении закладных деталей.

По расположению прутков арматуры в железобетонной конструкции:

• поперечную — предназначенную для предотвращения образования наклонных трещин;
• продольную — предназначенную для компенсации растягивающих или сжимающих нагрузок и предотвращения образования вертикальных трещин.

Рабочая, конструктивная и монтажная арматура вместе формируют арматурные каркасы и сетки.

Выбор диаметра арматуры для фундамента

Диаметр или толщина арматуры оказывает критически важное значение, как на прочность арматурного каркаса или сетки, так и на эффективность взаимодействия бетонного с арматурным скелетом.

В соответствии с нормативным документом СНиП 52-01-2003 «Бетонные и железобетонные конструкции» для обеспечения необходимой надежности строительной конструкции площадь сечения армирующих продольных элементов на срезе фундамента должна составлять не менее 0,1%. Т.е. площадь поперечного сечения стержней арматуры по отношению к общей площади фундамента в разрезе должна соотноситься как 0,001 к 1.

Для расчета количества прутов арматуры и их диаметра можно воспользоваться таблицей, приведенной ниже.

Как рассчитать количество прутков и диаметр арматуры для фундамента?

Для ленточного фундамента

Например, вам необходимо залить ленточный фундамент размером:

• Шириной 30 см (300 мм) и высотой 100 см (1000 мм).
• Площадь поперечного сечения фундамента будет составлять: 300 мм х 1000 мм = 300 000 мм2.
• Умножаем площадь поперечного сечения фундамента на коэффициент 0,001: 300 000 мм2 х 0,001 = 300 мм2 или 3 см2.
• Из приведенной выше таблицы видно, что минимальное количество прутов рифленой арматуры необходимое для обеспечения надежности фундамента: 6 прутов диаметром 8 мм или 4 прута диаметром 10 мм.
• Необходимо учитывать, что согласно пособию по проектированию «Армирование элементов монолитных железобетонных зданий», при длине фундамента по одной из сторон более 3 метров минимальный рекомендуемый диаметр арматуры должен составлять 12 мм.

Для плитного фундамента

Подход аналогичен расчету для ленточного фундамента, с учетом того, что для плитных фундаментов, необходимо учитывать продольное сечение фундамента.

Максимальный шаг монтажа стрежней арматуры для плитных фундаментов составляет 20 см!

Например, вам необходимо залить плитный фундамент размером:

• Шириной 600 см (6000 мм), длиной 800 см (8000 мм) и высотой 30 см (300 мм).
• Площадь продольного сечения фундамента будет составлять: 8000 мм х 300 мм = 2 400 000 мм2.
• Умножаем площадь продольного сечения фундамента на коэффициент 0,001: 2 400 000 мм2 х 0,001 = 2 400 мм2 или 24 см2.
• Из приведенной выше таблицы видно, что минимальное количество прутов арматуры необходимое для обеспечения надежности фундамента: 6 прутов диаметром 8 мм или 4 прута диаметром 10 мм.
• Из приведенной выше таблицы видно, что минимальное количество прутов арматуры необходимое для обеспечения надежности фундамента: 80 прутов диаметром 8 мм
• Так как длинна фундамента более 3 метров то нам необходима арматура диаметром 12 мм.

Для столбчатого фундамента

Для столбчатых фундаментов площадь поперечного сечения стержней арматуры по отношению к поперечной площади заливаемого столбчатой опоры должна соотноситься как 0,002 к 1, т.е. в 2 раза больше!

Для армирования опор столбчатого фундамента используют пространственные арматурные каркасы.

Применение различных типов и диаметров арматуры при заливке фундамента

В таблице, приведенной ниже, описаны рекомендации по использованию гладкой А1 и рифленой А3 арматуры в зависимости от их диаметра.

Как правило, пруты арматуры диаметром 6—8 мм используются в качестве монтажных, а с большим диаметром в качестве рабочей и конструктивной.

Диаметр арматуры, мм	Профиль арматуры	Применение
6	Гладкий А1, Рифленый А3	Монтажная
8		Монтажная, рабочая для буронабивных свай
10	Рифленый А3	Рабочая
12		Рабочая
14
16		Рабочая для больших зданий и сложных грунтов

 

В таблице, приведенной ниже приведены рекомендации по использованию композитной арматуры взамен стальной.

Характеристика	Стальная арматура класса АIII	Композитная арматура
Соответствие диаметров стальной и композитной арматуры при равных прочностных характеристиках, мм	8	4
	10	6
	12	8
	14	10
	16	12
	18	14
	20	16

 

• На сайте armatura-optom. by вы можете оформить оптовый заказ на поставку стальной рифленой и гладкой арматуры, композитной арматуры, вязальной проволоки.
• А на сайте металлобазы «Аксвил» вы можете купить арматуру для фундамента в розницу.

 

Смотрите также:

• Сортамент арматуры, виды и классы арматурного проката
• Теоретический вес рифленой арматуры А3.
• Теоретический вес сварной сетки.
• Теоретический вес гладкой арматуры А1.
• Online калькулятор арматуры.
• ГОСТЫ, СТБ и ТУ на арматуру.
• Расчет площади поперечного сечения строительной арматуры.
• Как армировать стяжку?
• Как армировать кладку из строительных блоков?
• Как армировать кладку из кирпича?

Введение в обучение с подкреплением: основы и реализация

Введение

Одним из самых фундаментальных вопросов в области обучения с подкреплением для ученых всего мира был вопрос «Как научиться новому навыку?». Желание понять ответ очевидно — если мы сможем понять это, мы сможем позволить человеческому роду делать то, о чем раньше даже не думали. С другой стороны, мы можем обучать машины, используя обучение с подкреплением, выполнять больше «человеческих» задач и создавать настоящий искусственный интеллект.

Хотя у нас пока нет полного ответа на поставленный выше вопрос, кое-что ясно. Независимо от навыка, мы сначала учимся, взаимодействуя с окружающей средой. Учимся ли мы водить машину или младенец учится ходить, обучение основано на взаимодействии с окружающей средой. Обучение на основе взаимодействия является основополагающей концепцией всех теорий обучения и интеллекта.

 

Повторное обучение

Сегодня мы рассмотрим обучение с подкреплением — целенаправленное обучение, основанное на взаимодействии с окружающей средой. Говорят, что обучение с подкреплением — это надежда настоящего искусственного интеллекта. И это правильно сказано, ведь потенциал, которым обладает Reinforcement Learning, огромен.

Обучение с подкреплением быстро развивается, создавая широкий спектр алгоритмов обучения для различных приложений. Поэтому важно знать методы обучения с подкреплением. Если вы не знакомы с обучением с подкреплением, я предлагаю вам ознакомиться с моей предыдущей статьей о введении в обучение с подкреплением и платформах RL с открытым исходным кодом.

После того, как вы поймете основные принципы, переходите к этой статье. К концу этой статьи у вас будет полное представление об обучении с подкреплением и его практической реализации.

 

П.С. Для реализации мы предполагаем, что у вас есть базовые знания Python. Если вы не знаете Python, вам следует сначала пройти это руководство

.

 

Содержание

1. Формулировка задачи обучения с подкреплением
2. Сравнение с другими методологиями машинного обучения
3. Фреймворк для решения задач обучения с подкреплением
4. Реализация обучения с подкреплением
5. Увеличение сложности
6. Ознакомьтесь с последними достижениями RL
7. Дополнительные ресурсы

 

1.

Формулировка задачи обучения с подкреплением

Обучение с подкреплением — это обучение тому, что делать и как преобразовывать ситуации в действия. Конечным результатом является максимизация числового сигнала вознаграждения. Учащемуся не говорят, какое действие предпринять, но вместо этого он должен выяснить, какое действие принесет максимальную награду. Давайте разберемся с этим на простом примере ниже.

Рассмотрим пример ребенка, который учится ходить.

Вот шаги, которые сделает ребенок, пока учится ходить:

1. Первое, что заметит ребенок, заметит как вы ходите. Вы используете две ноги, делая шаг за шагом, чтобы ходить. Усвоив это понятие, ребенок пытается копировать вас.
2. Но скоро он поймет, что прежде чем ходить, ребенок должен встать! Это вызов, который возникает при попытке ходить. Так что сейчас ребенку пытается встать, спотыкается и спотыкается, но все еще решительно настроен встать.
3. Тогда есть еще одно испытание, с которым нужно справиться. Встать было легко, но чтобы оставаться неподвижным  это совсем другая задача! Хватаясь за разреженный воздух в поисках опоры, ребенку удается удержаться на ногах.
4. Теперь настоящая задача для ребенка — начать ходить. Но проще сказать, чем на самом деле сделать. Есть так много вещей, о которых нужно помнить , например, сбалансировать вес тела, решить, какую ногу поставить следующей и куда ее поставить.

Звучит как сложная задача, верно? На самом деле немного сложно встать и начать ходить, но вы настолько привыкли к этому, что задача вас не смущает. Но теперь вы можете понять, как это сложно для ребенка.

Давайте формализуем приведенный выше пример, «постановка задачи» в примере для ходьбы , где ребенок является агентом пытающимся манипулировать средой (которая является поверхностью, по которой он ходит) на предпринимает действия (то есть идет) , и он/она пытается перейти из одного состояния (то есть каждый шаг, который он/она делает) в другое. Ребенок получает вознаграждение (скажем, шоколад) , когда он / она выполняет подмодуль задания (то есть делает пару шагов) и не получит никакого шоколада (также известное как отрицательное вознаграждение) , когда он / она не умеет ходить. Это упрощенное описание проблемы обучения с подкреплением.

Вот хорошее вводное видео по обучению с подкреплением.

 

2. Сравнение с другими методологиями машинного обучения

Обучение с подкреплением относится к более широкому классу алгоритмов машинного обучения. Ниже приведено описание типов методологий машинного обучения.

 

Давайте посмотрим на сравнение между RL и другими:

• Контролируемое обучение и обучение с подкреплением : В обучении с учителем есть внешний «супервайзер», который обладает знаниями об окружающей среде и делится ими с агентом для выполнения задачи. Но есть некоторые проблемы, в которых есть так много комбинаций подзадач, которые агент может выполнить для достижения цели. Так что создать «супервайзера» почти нецелесообразно. Например, в шахматах можно сделать десятки тысяч ходов. Поэтому создание базы знаний, в которую можно играть, — утомительная задача. В этих задачах целесообразнее учиться на собственном опыте и получать от него знания. Это основное различие, которое можно сказать об обучении с подкреплением и обучении с учителем. Как в обучении с учителем, так и в обучении с подкреплением существует соответствие между вводом и выводом. Но в обучении с подкреплением есть функция вознаграждения, которая действует как обратная связь с агентом, в отличие от обучения с учителем.
• Неконтролируемое обучение и обучение с подкреплением : В обучении с подкреплением существует сопоставление входных данных с выходными, которого нет в неконтролируемом обучении. При неконтролируемом обучении основная задача состоит в том, чтобы найти лежащие в основе модели, а не отображение. Например, если задача состоит в том, чтобы предложить пользователю новостную статью, алгоритм обучения без учителя будет просматривать похожие статьи, которые человек ранее читал, и предлагать кого-либо из них. В то время как алгоритм обучения с подкреплением будет получать постоянную обратную связь от пользователя, предлагая несколько новостных статей, а затем строит «граф знаний», какие статьи понравятся человеку.

Существует также четвертый тип методологии машинного обучения, называемый обучением с полуучителем , который, по сути, представляет собой комбинацию обучения с учителем и без учителя. Оно отличается от обучения с подкреплением тем, что аналогично обучению с учителем и полуучителем имеет прямое отображение, а подкрепление — нет.

 

3. Основа решения задач обучения с подкреплением

Чтобы понять, как решить задачу обучения с подкреплением, давайте рассмотрим классический пример задачи обучения с подкреплением — задачу о многоруком бандите. Во-первых, мы поймем фундаментальную проблему исследования и эксплуатации, а затем перейдем к определению структуры для решения проблем RL.

 

Предположим, у вас много игровых автоматов со случайными выплатами. Игровой автомат будет выглядеть примерно так.

Теперь вы хотите получить максимальный бонус от игровых автоматов как можно быстрее. Что бы вы сделали?

Один из наивных подходов может состоять в том, чтобы выбрать только один игровой автомат и целый день дергать за рычаг. Звучит скучно, но это может дать вам «некоторые» выплаты. При таком подходе вы можете сорвать джекпот (с вероятностью, близкой к 0,00000….1), но большую часть времени вы можете просто сидеть перед игровым автоматом и терять деньги. Формально это можно определить как чистая эксплуатация подход. Это оптимальный выбор? Ответ — нет.

Давайте рассмотрим другой подход. Мы могли бы дернуть за рычаг каждого игрового автомата и молить Бога, чтобы хотя бы один из них сорвал джекпот. Это еще один наивный подход, который заставит вас дергать за рычаги весь день, но даст вам неоптимальные выплаты. Формально этот подход является подходом чистого исследования .

Оба эти подхода не оптимальны, и мы должны найти правильный баланс между ними, чтобы получить максимальную награду. Говорят, что это дилемма исследования и эксплуатации обучения с подкреплением.

Сначала мы формально определяем структуру проблемы обучения с подкреплением, а затем перечисляем возможные подходы к решению проблемы.

Марковский процесс принятия решений:

Математическая основа для определения решения в сценарии обучения с подкреплением называется Марковский процесс принятия решений . Это может быть разработано как:

• Набор состояний, S
• Набор действий, А
• Функция вознаграждения,
р.
• Полис, №
• Значение, В

Мы должны выполнить действие (A) для перехода из начального состояния в конечное ( S ). Взамен получая вознаграждение (R) за каждое действие, которое мы предпринимаем. Наши действия могут привести к положительному или отрицательному вознаграждению.

Набор предпринятых нами действий определяет нашу политику (π), а вознаграждение, которое мы получаем взамен, определяет нашу ценность (V). Наша задача здесь состоит в том, чтобы максимизировать наше вознаграждение, выбрав правильную политику. Таким образом, мы должны максимизировать для всех возможных значений S на время t.

 

Проблема кратчайшего пути

Позвольте мне объяснить вам еще один пример.

Это представление задачи поиска кратчайшего пути. Задача состоит в том, чтобы добраться из пункта А в пункт F с наименьшими затратами. Числа на каждом ребре между двумя точками представляют стоимость прохождения расстояния. Отрицательная стоимость на самом деле является некоторой прибылью в пути. Мы определяем ценность как общую совокупную награду, когда вы выполняете политику.

Здесь,

• Набор состояний — это узлы, а именно {A, B, C, D, E, F}
• Необходимо перейти из одного места в другое, а именно {A -> B, C -> D и т. д.}
• Функция вознаграждения представляет собой значение, представленное преимуществом, т. е. стоимость
• Политика — это «способ» выполнения задачи, а именно {A -> C -> F}

Теперь предположим, что вы находитесь в точке А, единственным видимым путем является ваш следующий пункт назначения, а все, что находится за ним, на данном этапе неизвестно (так называемое наблюдаемое пространство).

Вы можете использовать жадный подход и выбрать наилучший следующий шаг, который идет от {A -> D} из подмножества {A -> (B, C, D, E)}. Точно так же теперь вы находитесь в месте D и хотите перейти в место F, вы можете выбрать из {D -> (B, C, F)}. Мы видим, что {D -> F} имеет наименьшую стоимость, и поэтому мы идем по этому пути.

Итак, здесь наша политика заключалась в том, чтобы взять {A -> D -> F}, и наше значение равно -120.

Поздравляем! Вы только что реализовали алгоритм обучения с подкреплением. Этот алгоритм известен как эпсилон жадный, , который буквально является жадным подходом к решению проблемы. Теперь, если вы (продавец) хотите снова перейти из пункта А в пункт F, вы всегда будете выбирать одну и ту же политику.

Другие способы передвижения?

Можете ли вы угадать, к какой категории относится наша политика, например (чистое исследование или чистое использование)?

Обратите внимание, что выбранная нами политика не является оптимальной. Нам придется немного «исследовать», чтобы найти оптимальную политику. Подход, который мы использовали здесь, — это обучение на основе политики, и наша задача — найти оптимальную политику среди всех возможных политик. Есть разные способы решить эту проблему, я кратко перечислю основные категории

• На основе политик, где наша цель – найти оптимальную политику
• На основе ценности, где наша цель — найти оптимальное значение, т. е. кумулятивное вознаграждение
• На основе действий, где мы фокусируемся на том, какие оптимальные действия следует предпринимать на каждом этапе

Я постараюсь подробно рассказать об алгоритмах обучения с подкреплением в будущих статьях.

4. Реализация обучения с подкреплением

Мы будем использовать алгоритм глубокого Q-обучения. Q-обучение — это алгоритм обучения, основанный на политике, с аппроксиматором функции в виде нейронной сети. Этот алгоритм использовался Google для победы над людьми в играх Atari!

Давайте посмотрим псевдокод Q-обучения:

1. Инициализировать таблицу значений ‘ Q(s, a)’ .
2. Наблюдать за текущим состоянием ‘ s’ .
3. Выберите действие ‘a’  для этого состояния на основе одной из политик выбора действия (например, эпсилон-жадный)
4. Выполните действие и наблюдайте за наградой ‘ r’ , а также новым состоянием ’ ‘ s’ .
5. Обновить значение состояния, используя наблюдаемое вознаграждение и максимально возможное вознаграждение для следующего состояния. Обновление производится по формуле и параметрам, описанным выше.
6. Установите новое состояние и повторяйте процесс, пока не будет достигнуто конечное состояние.

 

Простое описание Q-обучения можно резюмировать следующим образом:

Сначала мы посмотрим, в чем проблема Картпола, а затем перейдем к кодированию решения

Помню, в детстве я брал палку и пытался сбалансировать ее на одной руке. У меня и моих друзей было такое соревнование, где тот, кто балансирует больше времени, получал «награду» — шоколад!

Вот краткое видеоописание реальной системы тележки-шеста

Давайте закодируем!

Чтобы настроить наш код, нам нужно сначала установить несколько вещей,

Шаг 1.

Установите библиотеку keras-rl

Из терминала выполните следующие команды:

клон

 git https://github.com/matthiasplappert/keras-rl.git
cd keras-rl
установка python setup.py 

 

Шаг 2. Установите зависимости для среды CartPole

Предполагая, что у вас установлен pip, вам необходимо установить следующие библиотеки

 пункт установить h5py
пип установить тренажерный зал
 

 

Шаг 3: приступим!

Сначала мы должны импортировать необходимые модули

 импортировать numpy как np
импортный тренажерный зал

из keras.models импорт последовательный
из keras.layers импортировать Dense, Activation, Flatten
из keras.optimizers импорт Адама

из rl.agents.dqn импортировать DQNAgent
из rl.policy импортировать EpsGreedyQPolicy
из rl.memory импортировать SequentialMemory 

Затем установите соответствующие переменные

 ENV_NAME = 'CartPole-v0'

# Получите среду и извлеките количество действий, доступных в задаче Cartpole
env = спортзал. make(ENV_NAME)
np.random.seed(123)
env.seed(123)
nb_actions = env.action_space.n 

Далее мы строим очень простую модель нейронной сети с одним скрытым слоем.

Модель

 = последовательная ()
model.add(Flatten(input_shape=(1,) + env.observation_space.shape))
model.add (плотный (16))
model.add(Активация('relu'))
model.add (плотный (nb_actions))
model.add(Активация('линейная'))
печать (модель.резюме()) 

Далее мы настраиваем и компилируем наш агент. Мы устанавливаем нашу политику как Epsilon Greedy, и мы также устанавливаем нашу память как последовательную память, потому что мы хотим хранить результат выполненных нами действий и вознаграждения, которые мы получаем за каждое действие.

 политика = EpsGreedyQPolicy()
память = SequentialMemory (лимит = 50000, длина_окна = 1)
dqn = DQNAgent (модель = модель, nb_actions = nb_actions, память = память, nb_steps_warmup = 10,
target_model_update=1e-2, политика=политика)
dqn.compile (Адам (lr = 1e-3), метрики = ['mae'])

# Хорошо, теперь пришло время кое-чему научиться! Мы визуализируем тренировку здесь для галочки, но это сильно замедляет тренировку. 
dqn.fit(env, nb_steps=5000, визуализация=True, подробный=2) 

Теперь мы тестируем нашу модель обучения с подкреплением

 dqn.test(env, nb_episodes=5, визуализация=True) 

Это будет вывод нашей модели:

И вуаля! Вы только что построили бота для обучения с подкреплением!

 

5. Увеличение сложности

Теперь, когда вы ознакомились с базовой реализацией обучения с подкреплением, давайте приступим к решению еще нескольких задач, каждый раз понемногу увеличивая сложность.

 

Задача – Ханойские башни

Для тех, кто не знаком с игрой — она была изобретена в 1883 году и состоит из 3 стержней и ряда дисков последовательного размера (3 на рисунке выше), начиная с крайнего левого стержня. Цель состоит в том, чтобы переместить все диски с крайнего левого стержня на крайний правый стержень за наименьшее количество ходов . (Подробнее можно прочитать в википедии)

Если нам нужно отобразить эту проблему, давайте начнем с состояний:

• Исходное состояние – Все 3 диска в крайнем левом стержне (по порядку 1, 2 и 3 сверху вниз)
• Конечное состояние — Все 3 диска в крайнем правом стержне (по порядку 1, 2 и 3 сверху вниз)

 

Все возможные состояния: 

Вот наши 27 возможных состояний:

Все диски в шатуне	Один диск в стержне	(13) диски в шатуне	(23) диски в шатуне	(12) диски в шатуне
(123)**	321	(13)2*	(23)1*	(12)3*
*(123)*	312	(13)*2	(23)*1	(12)*3
**(123)	231	2(13)*	1(23)*	3(12)*
	132	*(13)2	*(23)1	*(12)3
	213	2*(13)	1*(23)	3*(12)
	123	*2(13)	*1(23)	*3(12)

Где (12)3* обозначает диски 1 и 2 в крайнем левом стержне (сверху вниз) 3 в среднем стержне, а * обозначает пустой крайний правый стержень

 

Числовое вознаграждение:

Поскольку мы хотим решить задачу за наименьшее количество шагов, мы можем присвоить награду -1 каждому шагу.

 

Политика:

Теперь, не вдаваясь в технические детали, мы можем отобразить возможные переходы между вышеуказанными состояниями. Например, (123)** -> (23)1* с вознаграждением -1. Он также может перейти к (23)*1

.

Если теперь вы видите параллель, каждое из этих 27 состояний, упомянутых выше, может представлять граф, аналогичный приведенному выше алгоритму кратчайшего пути, и мы можем найти наиболее оптимальные решения, экспериментируя с различными состояниями и путями.

 

Задача — Кубик Рубикса 3 x 3

Хотя я могу решить это и для вас, я бы хотел, чтобы вы сделали это сами. Следуйте той же мысли, которую я использовал выше, и у вас все будет хорошо.

Начните с определения начального состояния и конечного состояния. Затем определите все возможные состояния и их переходы вместе с вознаграждением и политикой. Наконец, вы должны быть в состоянии создать решение для сборки кубика Рубикса, используя тот же подход.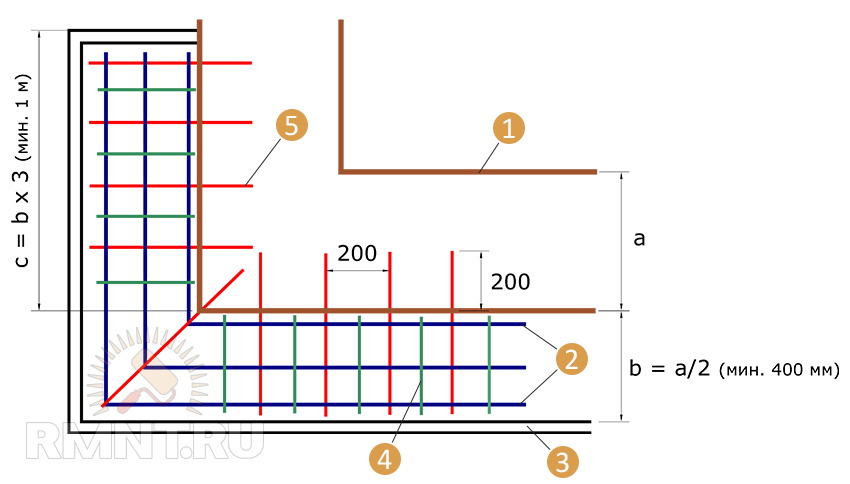

 

 

6. Взгляд на последние достижения в обучении с подкреплением

Как вы понимаете, сложность этого Куба Рубикса во много раз выше, чем у Ханойских башен. Вы также можете понять, как увеличилось количество возможных вариантов. Теперь подумайте о количестве состояний и вариантов в игре в шахматы, а затем в го! Google DeepMind недавно создал алгоритм глубокого обучения с подкреплением, который победил Ли Седоля!

Благодаря недавнему успеху в области глубокого обучения теперь акцент постепенно смещается на применение глубокого обучения для решения задач обучения с подкреплением. Недавно в новостях появилось сообщение о поражении Ли Седоля алгоритмом глубокого обучения с подкреплением, разработанным Google DeepMind. Подобные прорывы наблюдаются и в видеоиграх, где разработанные алгоритмы достигают точности человеческого уровня и выше. Исследования по-прежнему находятся на должном уровне, и промышленные, и академические вдохновители работают вместе, чтобы достичь цели по созданию более совершенных самообучающихся роботов

Источник

Ниже приведены некоторые основные домены, в которых было применено RL:

• Теория игр и многоагентное взаимодействие
• Робототехника
• Компьютерные сети
• Автомобильная навигация
• Медицина и
• Промышленная логистика.

Есть так много неизведанных вещей, и с нынешним повальным увлечением глубоким обучением, применяемым к обучению с подкреплением, определенно грядут прорывы!

Вот одна из последних новостей:

Рад поделиться новостями на #AlphaGo! pic.twitter.com/IT5HGBmYDr

— Демис Хассабис (@demishassabis) 4 января 2017 г.

 

7. Дополнительные ресурсы

Надеюсь, теперь у вас есть глубокое понимание того, как работает обучение с подкреплением. Вот несколько дополнительных ресурсов, которые помогут вам больше узнать об обучении с подкреплением

.

• Видео по обучению с подкреплением
• Книга по введению в обучение с подкреплением
• Awesome Reinforcement Learning Github repo
• Курс обучения с подкреплением Дэвида Сильвера

 

Конечные примечания

Надеюсь, вам понравилось читать эту статью. Если у вас есть какие-либо сомнения или вопросы, не стесняйтесь размещать их ниже. Если вы уже работали с обучением с подкреплением, поделитесь своим опытом ниже. В этой статье я хотел предоставить вам обзор обучения с подкреплением и его практической реализации. Надеюсь, вы найдете его полезным.

Учись, соревнуйся, взламывай и получай работу

Многоступенчатое обучение с подкреплением — Введение в обучение с подкреплением

Результаты обучения

1. Вручную применить n-шаговое приближение обучения с подкреплением для решения маломасштабных задач MDP

2. Разработка и внедрение n-шагового обучения с подкреплением для решения проблемы MDP среднего масштаба автоматически

3. Аргументация сильных и слабых сторон n-шагового обучения с подкреплением

Обзор

В предыдущих разделах этой главы мы рассмотрели два фундаментальных временных разностные (TD) методы обучения с подкреплением: Q-обучение и САРСА.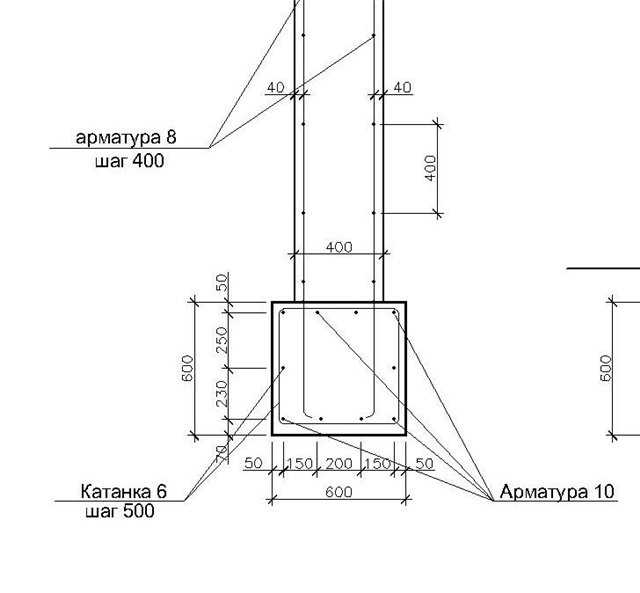

Эти два метода имеют некоторые недостатки в этом базовом формате:

1. В отличие от методов Монте-Карло, которые получают вознаграждение, а затем распространять это вознаграждение обратно, методы TD используют загрузку (они оценить будущее вознаграждение со скидкой, используя \(Q(s,a)\)), что означает что для проблем с редкими наградами может потребоваться много времени, чтобы чтобы награды распространялись по Q-функции.

2. Награды могут быть скудными, а это означает, что существует несколько состояний/действий, которые привести к ненулевым вознаграждениям. Это проблематично, потому что изначально Алгоритмы обучения с подкреплением ведут себя совершенно случайно и будут бороться за хорошие награды.

3. Оба метода оценивают Q-функцию \(Q(s,a)\), и самый простой способ модель это через Q-таблицу. Однако это требует от нас поддержания таблица размера \(|A| \times |S|\), которая непозволительно велика для любого нетривиальная проблема.

4. Использование Q-таблицы требует посещения каждого достижимого состояния много раз. раз и применяйте каждое действие много раз, чтобы получить точную оценку \(Q(s,a)\). Таким образом, если мы никогда не посещаем состояние \(s\), у нас нет оценки из \(Q(s,a)\), даже если мы посетили состояния, очень похожие на \(с\).

Чтобы обойти ограничения 1 и 2, мы рассмотрим n-шаговое обучение временной разности: методы «Монте-Карло» выполняют целые трассы, а затем распространяют вознаграждение, в то время как базовые методы TD рассматривают только вознаграждение на следующем шаге. , оценивая будущих подопечных. Вместо этого n-шаговые методы просматривают вознаграждение на \(n\) шагов вперед, прежде чем обновлять вознаграждение, а затем оценивают остаток. В следующих частях этих заметок мы рассмотрим методы смягчения ограничений 3 и 4.

n-шаговое обучение TD исходит из идеи, использованной на изображении ниже, от Sutton and Barto (2020). В методах Монте-Карло используются «глубокие резервные копии», когда выполняются целые трассировки, а вознаграждение передается обратно. Такие методы, как Q-обучение и SARSA, используют «неглубокие резервные копии», используя только вознаграждение за 1 шаг вперед. n-шаговое обучение находит золотую середину: обновляйте Q-функцию только после изучения вперед \(n\) шагов.

Рис. 1 Подходы к обучению с подкреплением (из Sutton and Barto (2020))

n-шаговое обучение TD

Мы рассмотрим n-шаговое обучение с подкреплением, в котором \(n\) — это параметр, который определяет количество шагов, которые мы хотим заглянуть вперед перед обновлением Q-функции. Таким образом, для \(n=1\) это просто «обычное» TD-обучение, такое как Q-обучение или SARSA. Когда \(n=2\), алгоритм смотрит на один шаг дальше непосредственной награды, \(n=3\) он смотрит на два шага дальше и т. д.

И Q-learning, и SARSA имеют n-шаговую версию. Мы рассмотрим n-шаговое обучение в более общем виде, а затем покажем алгоритм для n-шагового обучения. САРСА. Версия для Q-learning аналогична. 93 r_4+\ldots\]

Мы можем переписать это как:

\[ G_t = r_1 + \gamma(r_2 + \gamma(r_3 + \gamma(r_4 + \ldots))) \]

Если \(G_t\) значение, полученное на временном шаге \(t\), то

\[ G_t = r_t + \gamma G_{t+1} \]

В методах TD(0), таких как Q-learning и SARSA, мы не знаем \(G_{t+1}\) при обновлении \(Q(s,a)\), поэтому мы оцениваем с помощью начальной загрузки:

\[ G_t = r_t + \gamma \cdot V(s_{t+1}) \]

То есть награда все будущее с шага \(t\) оценивается как вознаграждение в \(t\) плюс расчетное (дисконтированное) будущее вознаграждение от \(t+1\). \(V(s_{t+1})\) есть оценивается с использованием максимальной ожидаемой отдачи (Q-обучение) или оценочное значение следующего действия (SARSA). 9n_t\) — это полное вознаграждение, усеченное в \(n\) шагов, в момент времени \(t\).

Основная идея n-шагового обучения с подкреплением заключается в том, что мы не обновляем Q-значение сразу после выполнения действия: ждем \(n\) шагов и обновляем его на основе n-шагового возврата.

Если \(T\) шаг завершения и \(t + n \geq T\), то мы просто используем полный награда.

В методах Монте-Карло мы идем до конца эпизода. Поиск по дереву Монте-Карло является одним из таких методов Монте-Карло, но есть другие, которые мы не покрываем. 9nQ(s_{\tau+n}, a_{\tau+n}).\]

Добавляет ожидаемую награду в будущем, если мы не в конце эпизода (если \(\tau+n < T\)).

Наконец, мы обновляем Q-значение:

\[Q(s_{\tau}, a_{\tau}) \leftarrow Q(s_{\tau}, a_{\tau}) + \alpha[G — Q(s_{\tau}, a_{\ тау}) ]\]

В приведенном выше правиле обновления мы используем обновление SARSA, но аналогичное обновление Q-learning.

n-ступенчатый SARSA

Хотя концептуально это не так уж сложно, алгоритм для выполнения n-шагового обучения должен хранить награды и наблюдаемые состояния для \(n\) шагов, а также отслеживать, какой шаг нужно обновить. Алгоритм для n-шагового SARSA показан ниже.

Алгоритм – n-шаговый SARSA

Ввод: MDP \(M = \langle S, s_0, A, P_a(s’ \mid s), r(s,a,s’)\rangle\), число шагов \(n\)
Вывод: Q-функция \(Q\)

Инициализировать \(Q\) произвольно; например, \(Q(s,a)=0\) для всех \(s\) и \(a\)

Повторить (для каждого эпизода)
\(\quad\quad\) Выбрать действие \(a\ ) для применения в \(s\) с использованием Q-значений в \(Q\) и алгоритма многорукого бандита, такого как \(\epsilon\)-жадный
\(\quad\quad\) \(ss = \ лангле с\рангле\)
\(\quad\quad\) \(as = \langle a\rangle\)
\(\quad\quad\) \(rs = \langle \rangle\)
\(\quad\quad\) Пока \ (ss\) не пусто
\(\quad\quad\quad\quad\) Если \(s\) не конечное состояние, то:
\(\quad\quad\quad\quad\quad\quad\) Выполнить действие \(a\) в состоянии \(s\)
\(\quad\quad\quad\quad\quad\quad\) Наблюдать за вознаграждением \(r\) и новым состоянием \(s’\)
\( \quad\quad\quad\quad\quad\quad\) \(rs \leftarrow rs + \langle r\rangle\)
\(\quad\quad\quad\quad\quad\quad\) Если \(s’ \) не является терминальным состоянием, то: 9n Q(s’, a’)\)
\(\quad\quad\quad\quad\quad\quad\) \(Q(ss_0, as_0) \leftarrow Q(ss_0, as_0) + \alpha[G — Q(ss_0, as_0)]\)
\(\quad\quad\quad\quad\quad\quad\) \(rs \leftarrow rs_{[1 : n + 1]}\)
\(\quad\quad \quad\quad\quad\quad\) \(ss \leftarrow ss_{[1 : n + 1]}\)
\(\quad\quad\quad\quad\quad\quad\) \(as \leftarrow as_ {[1 : n + 1]}\)
\(\quad\quad\quad\quad\) \(s \leftarrow s’\)
\(\quad\quad\quad\quad\) \(a \ стрелка влево а’\)

Это похоже на стандартную SARSA, за исключением того, что мы сохраняем последние \(n\) состояния, действия и награды; а также расчет вознаграждений за последние пять вознаграждений, а не только за одно. n\) вместо \(\gamma\). Почему? Это связано с тем, что предполагаемое вознаграждение в будущем составляет \(n\) шагов от состояния \(ss_0\). Награда \(n-step\) в \(G\) бывает первой. Затем мы выполняем фактическое обновление, которое обновляет пару состояние-действие \((ss_0, as_0)\), то есть \(n\)-шагов назад. 9{th}\) шаги эпизода; и отсутствие TD-оценки будущего вознаграждения на последних \(n\) шагах эпизода.

С вычислительной точки зрения это не намного хуже, чем одноэтапное обучение. Нам нужно сохранить последние \(n\) состояний, но пошаговое вычисление для n-шагов небольшое и единообразное, как и для 1-шага.

Пример — \(n\)-шаг обновления SARSA

Рассмотрим нашу простую задачу 2D-навигации, в которой мы не знаем переходов вероятности и вознаграждений. Первоначально алгоритм обучения с подкреплением должен будет выполнять поиск случайным образом, пока не найдет вознаграждение. Распространить это вознаграждение обратно на n шагов будет полезно.

Представьте себе первый эпизод, состоящий из следующего (очень удачного!) следа:

Предполагая, что \(Q(s,a)=0\) для всех \(s\) и \(a\), если мы пройдем эпизод помеченный эпизод, как будет выглядеть наша Q-функция для 5-шагового обновить с помощью \(\alpha=0. 4 rs_3 = 0,90 \cdot 1 = 1\\ & & Q((2,2, справа) = 0 + 0,5[1 \cdot 1 — 0] = 0,5 \конец{массив} \)

В этот момент больше не осталось состояний для обновления, поэтому внутренний цикл завершается, и мы начинаем новый эпизод.

Реализация

Ниже приведена реализация на Python n-шагового обучения временным различиям. Сначала мы реализуем абстрактный суперкласс NStepReinforcementLearner , который содержит большую часть кода, который нам нужен, за исключением той части, которая определяет значение состояния \(s’\) в обновлении Q-функции, которое оставлено подклассу, чтобы мы могли поддержка как n-шагового Q-обучения, так и n-шагового SARSA:

 класс NStepReinforcementLearner:
    def __init__(self, mdp, bandit, qfunction, n, альфа=0.1):
        self.mdp = mdp
        self.bandit = бандит
        self.alpha = альфа
        self.qфункция = qфункция
        селф.n = n
    def выполнить (я, эпизоды = 100):
        для _ в диапазоне (эпизоды):
            состояние = self. mdp.get_initial_state()
            действия = self.mdp.get_actions (состояние)
            action = self.bandit.select(состояние, действия, self.qfunction)
            награды = []
            состояния = [состояние]
            действия = [действие]
            в то время как len(состояния) > 0:
                если не self.mdp.is_terminal (состояние):
                    (следующее_состояние, вознаграждение) = self.mdp.execute (состояние, действие)
                    награды += [награда]
                    next_actions = self.mdp.get_actions (следующее_состояние)
                    если не self.mdp.is_terminal(next_state):
                        next_action = self.bandit.select(
                            next_state, next_actions, self.qfunction
                        )
                        состояния += [next_state]
                        действия += [следующее_действие]
                если len(вознаграждения) == self.n или self.mdp.is_terminal(состояние):
                    n_step_rewards = сумма(
                        [
                            self. mdp.discount_factor ** i * вознаграждение[i]
                            для i в диапазоне (len (вознаграждения))
                        ]
                    )
                    если не self.mdp.is_terminal (состояние):
                        следующее_состояние_значение = self.state_value(следующее_состояние, следующее_действие)
                        n_step_rewards = (
                            n_step_rewards
                            + self.mdp.discount_factor ** self.n * next_state_value
                        )
                    q_value = self.qfunction.get_q_value(
                        состояния[0], действия[0]
                    )
                    self.qfunction.update(
                        состояния [0],
                        действия[0],
                        self.alpha * (n_step_rewards - q_value),
                    )
                    награды = награды [1 : self.n + 1]
                    состояния = состояния [1 : self.n + 1]
                    действия = действия [1 : self. n + 1]
                состояние = следующее_состояние
                действие = следующее_действие
    """ Получить значение состояния """
    def state_value (я, состояние, действие):
        абстрактный
 

Мы наследуем от этого класса для реализации n-шагового алгоритма Q-обучения:

 из импорта n_step_reinforcement_learner NStepReinforcementLearner
класс NStepQLearning (NStepReinforcementLearner):
    def state_value (я, состояние, действие):
        (_, max_q_value) = self.qfunction.get_max_q (состояние, self.mdp.get_actions (состояние))
        вернуть max_q_value
 

Пример — 1-этапное Q-обучение против 5-этапного Q-обучения

Используя интерактивную графику ниже, мы сравниваем одноэтапное и пятиэтапное Q-обучение в течение первых 20 эпизодов обучения в задаче GridWorld. При использовании одноэтапного Q-обучения достижение награды информирует только о состоянии, из которого оно было достигнуто в первом эпизоде; тогда как для 5-шагового Q-обучения он информирует о предыдущих пяти шагах. Затем, во втором эпизоде, если какое-либо действие достигает состояния, которое было посещено, оно может получить доступ к TD-оценке для этого состояния. В 5-этапном Q-обучении есть пять таких состояний; и только одно в 1 шаге Q-обучения. На всех последующих итерациях больше шансов встретить состояние с TD-оценкой, и эти оценки лучше информированы. Конечным результатом является то, что оценки «распространяются» по Q-таблице быстрее:

Значения

n

Можем ли мы просто увеличить \(n\) до бесконечности, чтобы получить вознаграждение за всю трассировку? Выполнение этого, которое называется симуляцией Монте-Карло , на практике работает не так хорошо. По сути, у нас больше не будет оценок TD в правиле обновления, что приводит к большей дисперсии в обучении.

Тогда какое значение для \(n\) будет лучшим? К сожалению, теоретически лучшего значения для \(n\) не существует. Это зависит от конкретного приложения и функции вознаграждения, которая обучается.