Что такое угол? Определение, виды, как обозначают, примеры
Поможем понять и полюбить математику
Начать учиться
118.2K
Знания школьной геометрии пригодятся в самых неожиданных ситуациях: во время ремонта, при рисовании граффити или чтобы нарезать пирог. В этой статье узнаем все про углы.
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
Что такое вершина и стороны угла
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.
Иногда встречается обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Прямой угол — это угол, стороны которого перпендикулярны друг другу.
Прямой угол всегда равен 90°.
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол, показано на первой картинке.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.
Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.
Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.
Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.
Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:
- ∠AOC = ∠AOB − ∠COB,
- ∠COB = ∠AOB − ∠AOC.
Запоминаем!
Угол называется прямым, если он равен 90°, острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол равен 180°.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.
- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.
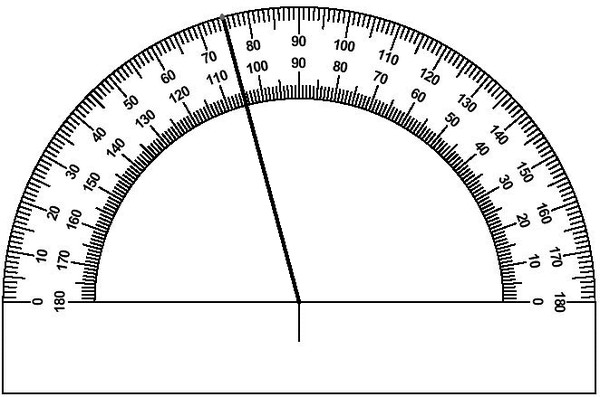
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот как он выглядит:
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается ´.
Секунда
— 1/60 часть минуты. Обозначается ´´.Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.
Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.
Равные углы имеют равную градусную меру.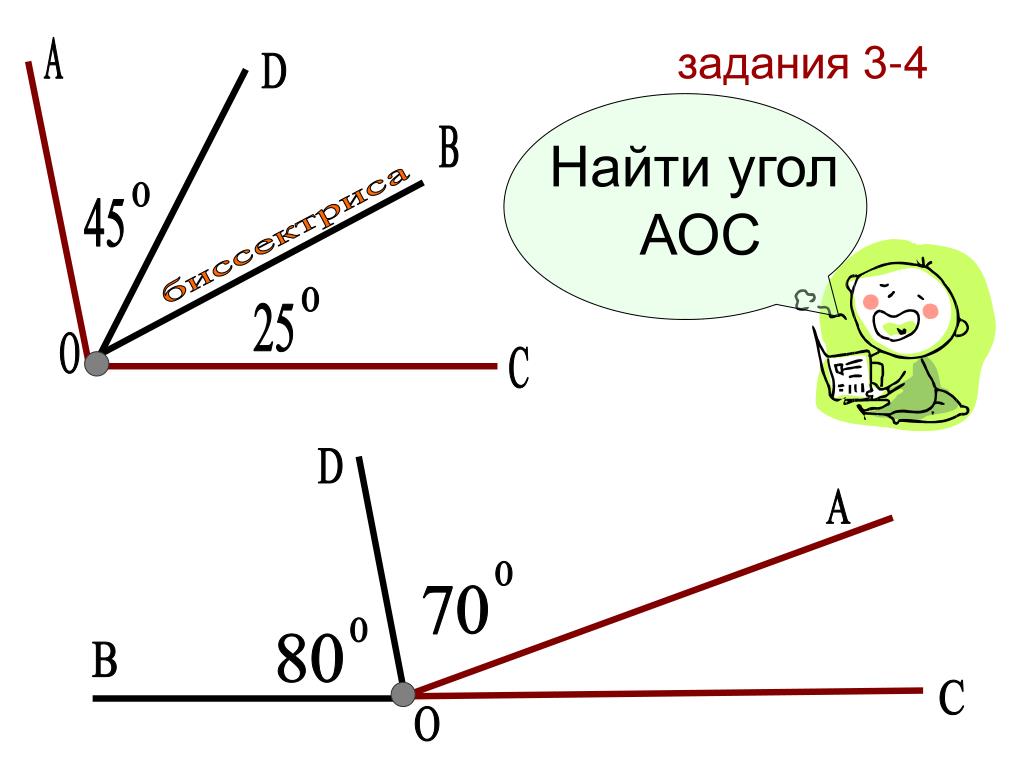
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
На чертеже отмечены три неравных угла:
Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
259.3K
Наибольший общий делитель (НОД), свойства и формулы
К следующей статье
Неполные квадратные уравнения
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Радиан, Углы больше 360 градусов, Положительные и отрицательные углы
Угол: °πrad =
Преобразовать в: радианы0 — 360°положительноеотрицательное
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами.
На картинке видны 4 разных угла, образованных пересечением прямых AB и CD
Обычно углы измеряются в градусах, что обозначается как °.
Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°).
Таким образом, градус — это $\frac{1}{360}$ круга.
Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.
Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.
Объект описал $2\frac{7}{9}$ кругов
Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.
В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.
Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)
Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360.
Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.
Пример 3
1.
Найти соответствующий положительный угол
a) -35°
b) -60°
c) -180°
d) — 670°
2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°
2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°
Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга.
{\circ}$
c) 1 рад = 57,3°
$2,4 = \frac{2,4 \times 57,3}{1} = 137,52$
Отрицаетльные углы и углы больше, чем $2\pi$ радиан
Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2\pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2\pi$.
Пример 5
1. Преобразовать $-\frac{3}{4}\pi$ и $-\frac{5}{7}\pi$ в позитивные углы в радианах.
Решение
Прибавляем к углу $2\pi$
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4}\pi$
$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2}{7}\pi$
Когда объект вращается на угол больший, чем $2\pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2\pi$, результат равен или меньше, но как можно ближе к данному числу.
Пример 6
1.
Найти количество кругов пройденных объектом при данных углах
a) $-10\pi$
b) $9\pi$
c) $\frac{7}{2}\pi$
Решение
a) $-10\pi = 5(-2\pi)$;
$-2\pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.
b) $9\pi = 4(2\pi) + \pi$, $\pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки
c) $\frac{7}{2}\pi=3,5\pi=2\pi+1,5\pi$, $1,5\pi$ равно три четверти цикла $(\frac{1,5\pi}{2\pi}=\frac{3}{4})$
объект прошел один и три четверти цикла против часовой стрелки
и классификация NEMA
A: Классификация света NEMA берет угол луча света и группирует его в одну из 7 категорий от очень узкого прожектора до очень широкой диаграммы направленности. Это помогает определить типы света и их идеальное использование.
Угол луча NEMA Классификация Название
От 10° до 18° I (один или 1) Очень узкий
От 18° до 29° II (также известный как два или 2) Узкий
От 29° до 46° III ( также три или 3) Средне-узкий
От 46° до 70° IV (то есть четыре или 4) Средний
От 70° до 100° V (также известный как пять из 5) Средне-широкий
От 100° до 130° VI (также известный как шесть или 6) Широкий
От 130°+ VII (также известный как семь или 7) Очень широкий
Эти классификации NEMA часто сокращаются, чтобы выглядеть примерно как 5H5V.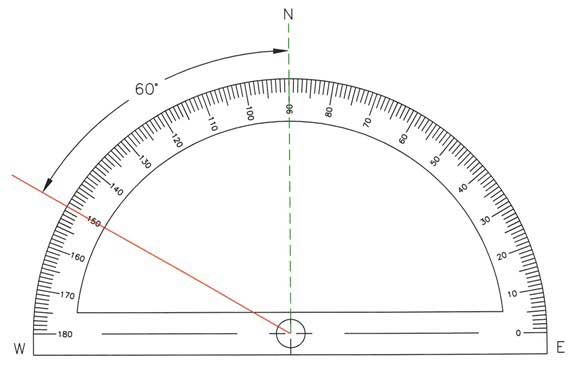
Это соответствует 5 горизонтальным и 5 вертикальным из шаблона выше. Многие огни, такие как спортивные, стадионные и высокие мачты, просто указаны как NEMA 3, что указывает на круглую форму.
Официальное правило расчета светового луча: освещенность составляет 10% или выше в процентах от максимума; Итак, если его угол луча 30 градусов, но 9% шире, это все еще 30-градусный луч. Кровотечение в пределах спецификации. Это правило также верно для паттернов H + V, где каждое направление должно соответствовать этому числу.
ОПИСАНИЕ ОБЫЧНОГО РАССЕЯНИЯ ЛУЧА
Ультрапрожектор 1х2В или просто NEMA I
Традиционно очень сложно сделать, это не было обычным явлением до появления более новых светодиодных фонарей для стадионов. В фонариках часто использовался трюк с вогнутой выпуклостью для создания этого узора, но не настоящий NEMA из-за неточного рисунка. Современные светодиоды могут создавать диаграмму направленности 12, 15 или 20 градусов с очень высокой степенью точности.
Они используются для очень дальних приложений.
Прожектор 3х4В или просто NEMA III
Самая распространенная 1500-ваттная спортивная зажигалка HID за последние 40 лет, а теперь в эту категорию попадают и 500-ваттные стадионные светильники. NEMA III было довольно легко создать с помощью большого металлического отражателя вокруг газоразрядной лампы. Этот луч отлично работает на высоте 40-60 футов, что делает его таким популярным. См. руководство покупателя и видео о светодиодных светильниках для стадионов здесь
4h5V или NEMA IV
Общий угол луча в различных светильниках. 60-градусные лучи можно найти как в высоких пролетах, так и в некоторых спортивных светильниках;
H5V3 широкий, короткий Рисунок
Увеличение горизонтального рисунка при сохранении вертикального начинает формировать свет. Наиболее распространенным выражением этого является уличное освещение. Похож на широкий свет Типа II вверх и вниз по улице, но немного вперед, чтобы не ослеплять соседей.
h4V5 УЗКИЙ ВЫСОКИЙ
Перевернутый с высоким рисунком для поражения зданий и знаков. Не распространен, и обычно его нужно заказывать, но все же имеет свое применение.
ШИРОКИЙ РАСПРЕДЕЛЕНИЕ ПОТОКА H5V5
Часто встречающийся под углом 90 градусов, это популярный угол освещения склада для высоты около 30-40 футов, чтобы направить больше света на землю.
H6V6 ULTRA WIDE FLOOD
Самый распространенный широкоугольный прожектор, обеспечивающий широкий охват. Ожидайте этого на большинстве жилых настенных светильников и небольших прожекторах. Популярные идут в охват.
СРАВНЕНИЕ С МОДЕЛЯМИ СВЕТА IES
В таблице ниже представлена классификация светильников IES. Почти все наши светодиодные фонари для парковки относятся к типу III или T3. T3 очень эффективен, потому что он широкий, и вы можете наклонить его, чтобы увеличить бросок вперед
Можно заказать любой из этих шаблонов. Обычно мы не рекомендуем тип V, так как большая часть света падает на веху или крепление.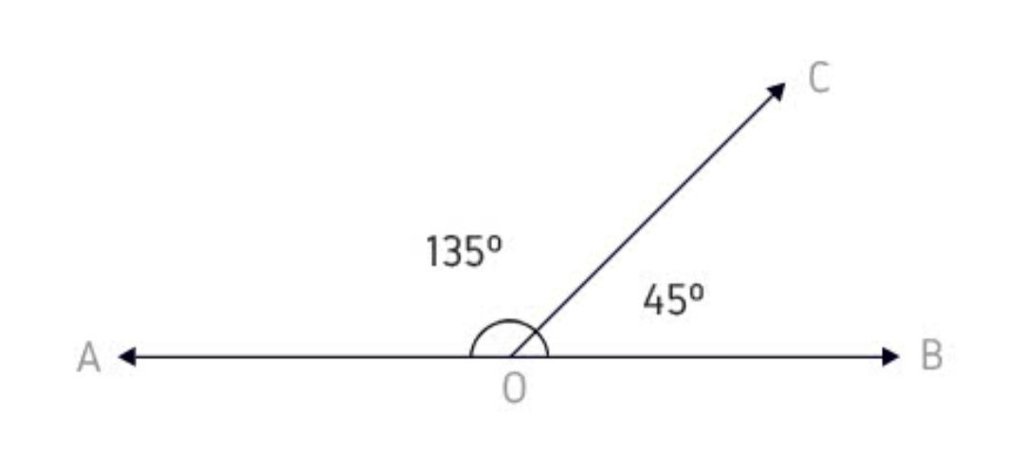
Лучше использовать 2 небольших светильника.
НАИЛУЧШИЕ ПРАКТИКИ ДЛЯ ПРОЕКТИРОВАНИЯ ОСВЕЩЕНИЯ
- Более узкие лучи для дальних лучей
- Средние лучи для стандартного освещения
- Широкий угол для близких расстояний
- Всегда думайте об однородности как вертикальных, так и горизонтальных фут-кандлей
- 4 соответствие небу, когда это возможно
- Будьте в курсе рейтингов BUG и того, как они могут или не могут повлиять на ваш проект
Позвоните любому из наших экспертов сегодня для бесплатной консультации по световому дизайну.
Узоры плитки и макеты
Различные типы рисунков на плитке
Где бы вы ни укладывали плитку в своем доме, наши специалисты из магазина плитки всегда готовы помочь вам выбрать красивый рисунок — неброский или привлекающий внимание — который украсит вашу комнату.
1. Елочка
Этот рисунок состоит из V-образных рядов плиток, расположенных под углом 45 градусов.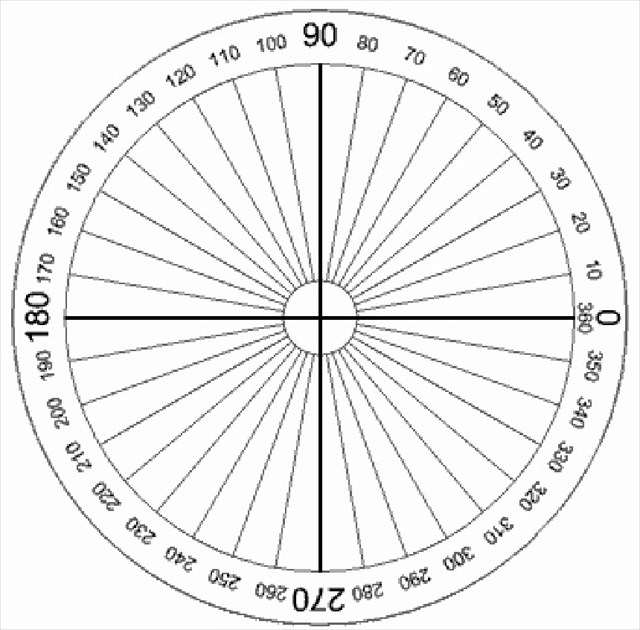
Эта раскладка представляет собой классический, но более наглядный способ укладки как крупной, так и мелкой прямоугольной плитки.
Плитка метро, популярная на фартуках, достигает новых высот стиля в елочке. Контрастный цвет затирки подчеркивает уникальный дизайн.
2. Кирпич со смещением/в шахматном порядке
Также известный как бегущая связь, этот общий образец кирпичной кладки имеет начало каждой плитки в центре плитки под ней. Это чистая и классическая раскладка плитки метро на стенах и полу.
Плитка под кирпич в этой планировке создает индустриальную атмосферу в вашем помещении. Этот узор также подчеркивает аутентичность плитки ручной работы.
3. Смещение 1/3
Каждая плитка в этом шаблоне смещает плитку под ней на одну треть своей длины, создавая эффект ступенчатой диагонали. Этот макет часто используется с одно-, двух- или трехцветными рисунками.
Плитка под дерево и другие дощатые плиты часто укладываются с использованием этой схемы.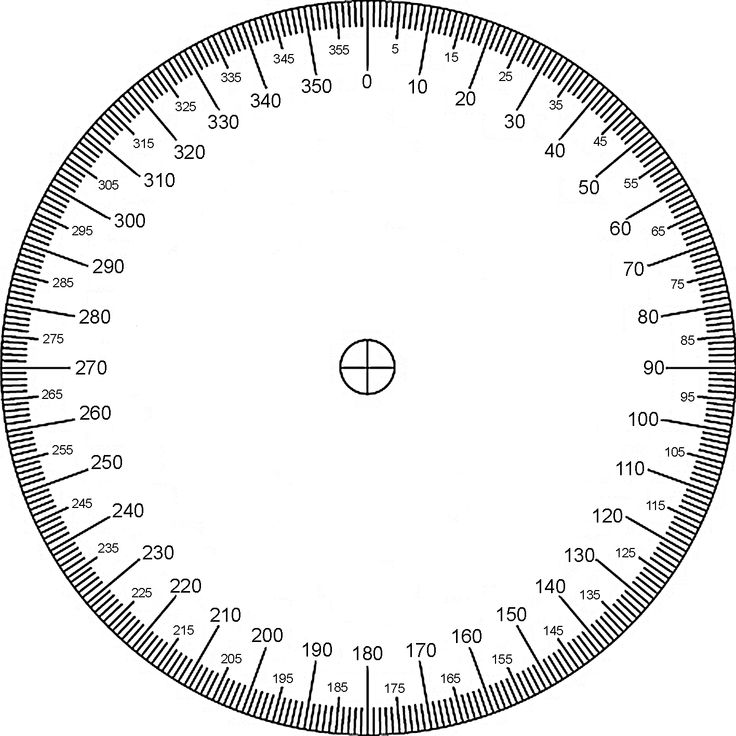
На самом деле, некоторые плитки большого формата должны быть смещены на 1/3 вместо этого, чтобы установка была надежной.
4. Сетка (уложенная)
Этот макет представляет собой базовый шаблон, в котором квадратные плитки расположены по прямой линии, чтобы создать простой и чистый вид. Прямоугольная плитка в таком расположении выглядит современно и чисто.
Для более традиционного вида укладывайте классические квадратные плитки в виде сетки. Акцент в рамке превращает этот фартук в выразительный элемент.
5. Вертикальная установка
В этом шаблоне плитки уложены вертикально, подчеркивая высоту вашего пространства, делая стены выше. Плитка метро внезапно обретает новую жизнь и геометрическую привлекательность в этом макете.
Крупноформатная плитка, уложенная вертикально, служит для расширения стен и пола в обоих направлениях. Добавьте текстуру, и этого достаточно, чтобы полностью белая стена вышла на новый уровень.
6. Вертушка (классики)
Этот шаблон использует меньшую квадратную плитку в каждом углу большего квадрата, чтобы имитировать внешний вид вращающейся вертушки.
Эта планировка является популярным рисунком напольного покрытия, особенно с керамической плиткой или в небольших ванных комнатах.
Тонкий рисунок, созданный компоновкой вертушки, дает возможность включить акцентный цвет или плитку в другую часть комнаты, связывая весь вид воедино.
7. Случайный
Возможности дизайна безграничны, когда у вас есть свобода творчества. Такая планировка идеально подходит для нестандартных пространств. Поэкспериментируйте с тремя, четырьмя и более цветами, чтобы произвести сильное впечатление.
Проявите творческий подход и установите плитку в макете без четкого рисунка. Создайте смелый и графический интерес, используя черно-белые оттенки.
8. Версаль (французский)
В этом элегантном узоре используется сочетание квадратных и прямоугольных плиток, что создает повторяющийся рисунок, напоминающий головоломку. Нам нравится использовать Версальскую планировку на полах из натурального камня, такого как травертин.
Модель Versailles приобретает современный вид в холодном монохромном пространстве. Смешанные и подобранные размеры плитки привлекают внимание к полу, не отвлекая внимания от остального пространства.
9. Плетение корзины (геометрическое)
В этом вневременном дизайне используется мозаика из плиток с крошечными квадратами, которые напоминают движение плетеной корзины.
Мозаика корзиночного переплетения обеспечивает мягкий рисунок и может быть оформлена в традиционном или современном стиле в зависимости от окружающих плиток и декора.
10. Диагональ (алмаз)
В этом макете используются квадратные плитки, уложенные под углом 45 градусов. Отличный способ сделать ваши полы шире, мы также любим его для стен и фартуков.
Акцент на фоторамке — всегда хорошая идея. Укладывая согласованные плитки под углом, вы создаете тонкий интерес, не отвлекая от основного цвета.
11. Шеврон
Подобно елочке, в этом макете более короткий конец плитки выстроен в линию, образуя скошенный стык под углом 45 градусов.