Высчитать площадь прямоугольника: Запишите формулу площади квадрата со стороной а и б. Вычислите площадь прямоугольника при а=2, 5...

Содержание

Площадь прямоугольника формулы и калькулятор

{S = a \cdot b}

Найти площадь прямоугольника

через сторонычерез сторону и диагональдиагонали и угол между нимичерез сторону и периметрчерез сторону и радиус описанной окружностичерез радиус описанной окружности и угол между диагоналями

Сторона a

ммсмдммкмдюймы (in)футы (ft)

Сторона b

ммсмдммкмдюймы (in)футы (ft)

Результат в

мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)

Виджет

Ссылка на расчет

Сообщить об ошибке

Сохранить расчет

Печатать

Найти площадь прямоугольника вы сможете с помощью калькуляторов или по формулам вручную.

Для этого мы подготовили 6 формул и калькулятор, который позволяет произвести расчет по любой из них.

Прямоугольник — четырехугольник, у которого все углы равны 90° (прямые).

Содержание:

калькулятор площади прямоугольника
формула площади прямоугольника через стороны
формула площади прямоугольника через сторону и диагональ
формула площади прямоугольника через диагонали и угол
формула площади прямоугольника через сторону и периметр
формула площади прямоугольника через сторону и радиус описанной окружности
формула площади прямоугольника через радиус описанной окружности и угол между диагоналями
примеры задач

Формула площади прямоугольника через стороны

S = a \cdot b

a, b — стороны прямоугольника (длина и ширина)

Формула площади прямоугольника через сторону и диагональ

S=a \cdot \sqrt{d^2 — a^2}

d — диагональ прямоугольника

a — сторона прямоугольника

Формула площади прямоугольника через диагонали и угол

S = \dfrac{1}{2} \cdot d^2 \cdot \sin(\alpha)

d — диагональ прямоугольника

α — угол между диагоналями

Формула площади прямоугольника через сторону и периметр

S = \dfrac{a \cdot P — 2a^2}{2}

a — сторона прямоугольника

P — периметр прямоугольника

Формула площади прямоугольника через сторону и радиус описанной окружности

S = a \cdot \sqrt{4R^2 — a^2}

R — радиус описанной окружности

a — сторона прямоугольника

Формула площади прямоугольника через радиус описанной окружности и угол между диагоналями

S = 2R^2 \cdot \sin{\alpha}

R — радиус описанной окружности

α — угол между диагоналями

Примеры задач на нахождение площади сектора круга

Задача 1

Найдите площадь прямоугольника диагональ которого равна 10 см, а угол между диагоналями равен 30°. 2$.

Диагонали разделяют прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести одну диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.

Диагонали не являются биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.

Рис. 4. Рисунок к утверждению

Что мы узнали?

Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также не стоит забывать, что если в задании разные единицы измерения сторон, то необходимо перевести их одну.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Dima Erlichenkov
10/10

Оценка статьи

4.4

Средняя оценка: 4.4

Всего получено оценок: 163.

А какая ваша оценка?

Какая формула площади прямоугольника и квадрата?

Менсурация — греческое слово, означающее «измерение». Измерение — это раздел математики, который включает в себя вычисление геометрических фигур, таких как квадраты, прямоугольники, конусы, цилиндры и т. д. С помощью измерения можно научиться вычислять площадь, параметр, площадь поверхности и т. д., которые являются основными почти всех вычислений в области математики. Теперь давайте начнем с самой основной формулы измерения, т.е. Площадь. Давайте сначала разберемся, что такое область.

Площадь

Площадь – это размер поверхности или объем пространства, занимаемый замкнутой областью. Он рассчитывается для 2D-фигур и выражается в таких единицах, как м ² , см ² и т. д. Единицей площади всегда является квадратная единица. Обозначается буквой А. На приведенной ниже диаграмме показаны примеры геометрических фигур вместе с их расчетной площадью:

Давайте теперь посмотрим на формулу для расчета площади прямоугольника

Какова формула площади квадрата и прямоугольника?

Прямоугольник представляет собой геометрическую фигуру с четырьмя сторонами, каждый угол которой равен 90°.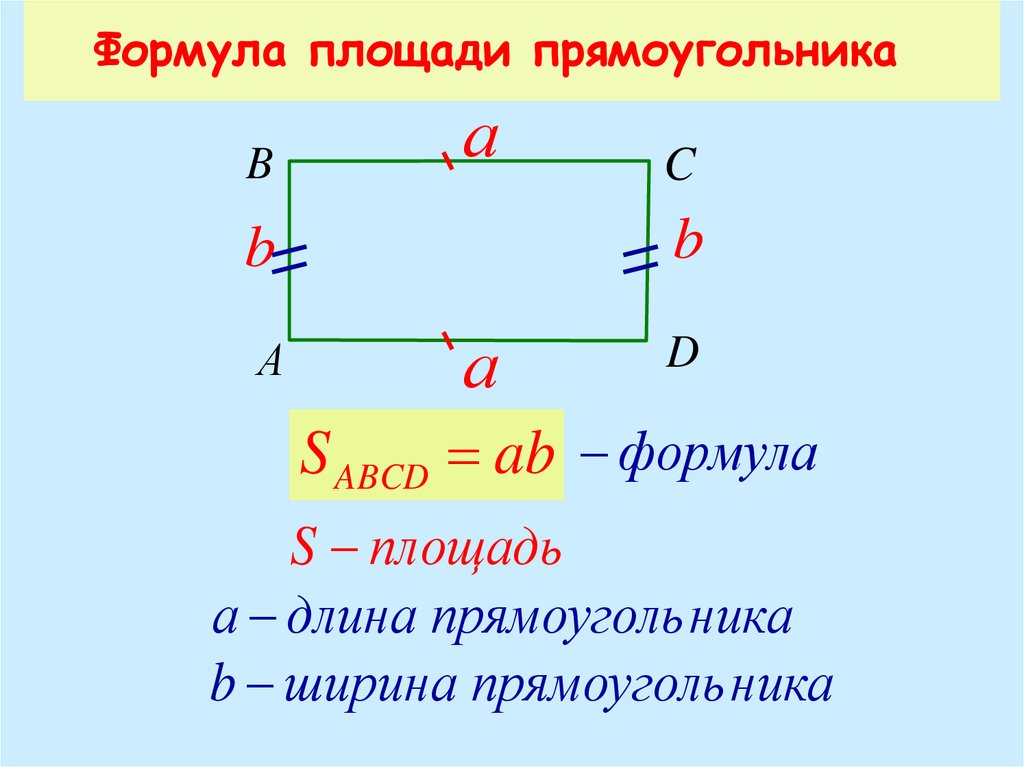 Из четырех сторон две стороны прямоугольника равны и параллельны, причем одна сторона длиннее другой. Прямоугольник выглядит так, как показано на рисунке ниже:

Площадь прямоугольника

На приведенном выше рисунке длинная сторона представляет собой длину, а более короткая сторона представляет собой ширину прямоугольника.

Формула

Формула для вычисления площади прямоугольника может быть получена с помощью следующих шагов:

Длина и ширина (Ширина) прямоугольника должны быть известны заранее.
Длина и ширина умножаются, и в результате получается искомая площадь.
Единицей площади является квадрат единицы его длины и ширины

Из приведенных выше шагов формула прямоугольника может быть записана следующим образом.

Площадь прямоугольника (A) = длина (L) × ширина (B), где L — длина прямоугольника, а B — ширина прямоугольника.

Примечание Если единицы длины и ширины не совпадают, их следует преобразовать в одну единицу. Например, Если длина в см, а ширина в м, то обе стороны следует изменить либо на м, либо на см.

Свойства прямоугольника

Противоположные стороны прямоугольника равны и параллельны.
Диагональ одинаковой длины.
Все углы равны 90°.
Диагонали прямоугольника делят друг друга пополам.

Квадрат

Квадрат — это геометрическая фигура, все четыре стороны которой имеют одинаковую длину. Каждая сторона образует угол 90°. Все четыре стороны квадрата равны и параллельны. Квадрат — это то же самое, что и прямоугольник, с той лишь разницей, что у квадрата все стороны равны. Квадрат выглядит так, как показано на рисунке ниже:

Площадь квадрата

Формула

Формула для вычисления площади квадрата может быть записана следующим образом:

Площадь квадрата (A) = Длина = Ширина = a × a = a ² где, а — сторона квадрата.

Свойства квадрата

Все стороны квадрата имеют одинаковую длину.
Углы каждой стороны равны, т.е. 90 градусов
Противоположные стороны квадрата параллельны.
Длины диагоналей равны.

Примеры задач

Вопрос 1: Найдите площадь прямоугольника, длина которого 5 см, а ширина 2 см.

Solution:

Given,
Length = 5cm
Breadth = 2cm
Formula:
A = Length × Breadth
A = 5cm × 2cm = 10cm ²

Question 2: Найдите площадь прямоугольника, длина и ширина которого равны 10 см и 0,5 м соответственно.

Решение:

, дано,
Длина = 10 см
ШАНА = 0,5 м
Давайте сначала изменить ширину в CM
1M = 100 см
Флария = 0,5 × 100 = 50c
. :
A = длина × ширина = 10 × 50 = 500 см ²

Вопрос 3: Найдите площадь квадрата со стороной 4 м.

Решение:

Дано, a = 4m
A = a ² = (4) ² = 16м ²

Вопрос 4: Найдите площадь квадратного участка со стороной 32см.

Решение:

Дано, a = 32 см
A = A ² = (32) ² = 1024 см ²

Площадь прямоугольника (выборки выборки)

^{0
Область прямоугольника (выборки выборки)
^{0
. область — это навык, который можно применять во многих реальных ситуациях. Вычисления площади выполняются для таких сценариев, как определение количества плитки, необходимой для покрытия дна бассейна, количества оберточной бумаги, необходимой для упаковки подарка, или площади вашего заднего двора. Подобные ситуации потребуют использования расчетов площади поверхности.
Площадь прямоугольника Примеры вопросов
При определении площади прямоугольника можно применить формулу $A=l\×w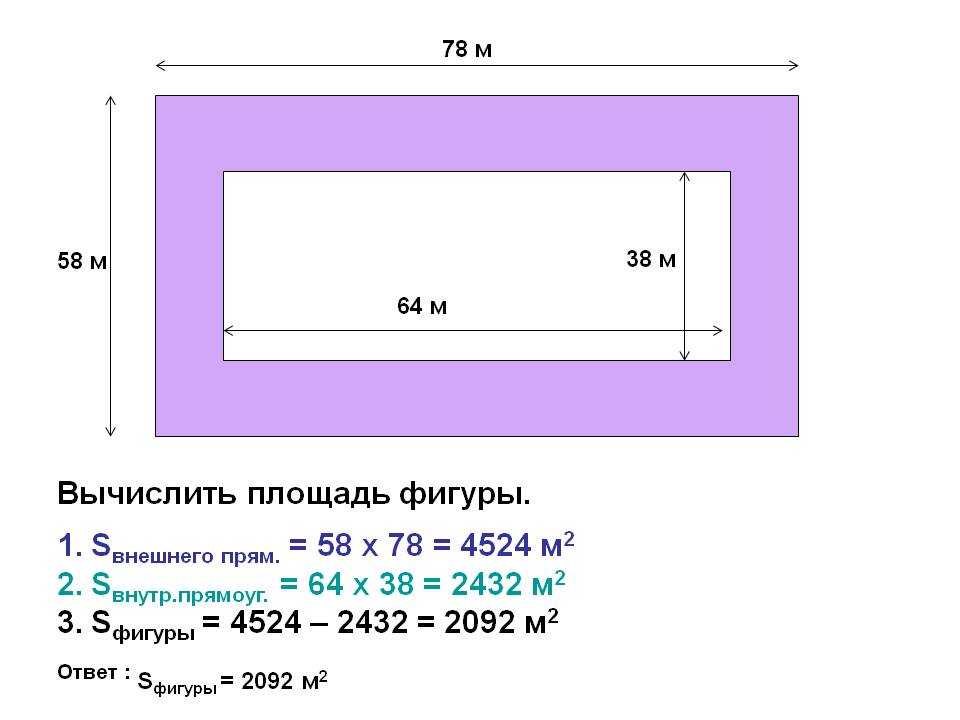$. A представляет площадь, l представляет длину, а w представляет ширину. Например, прямоугольник ниже имеет длину 32 метра и ширину 20 метров. Площадь прямоугольника можно вычислить путем умножения $l\times w$ или $32\times20$, что равно 6400. Единицы, связанные с площадью поверхности, всегда будут единицами в квадрате. Площадь является результатом умножения двух измерений, длины и ширины, которые можно представить как степень числа 2. В этом случае наш ответ будет 640 м ² .
Рассмотрим следующее:
Вы хотите посадить траву на своем новом заднем дворе, и в настоящее время у вас есть 645 квадратных футов дерна. Вы хотите определить, достаточно ли травы, чтобы покрыть весь двор, поэтому вам нужно сравнить площадь дерна с площадью вашего двора. Ваш двор имеет длину 25 футов и ширину 30 футов. У вас достаточно дерна, чтобы покрыть весь двор?
Это сценарий, в котором можно применить формулу площади прямоугольника. Длина двора 30 футов, ширина 20 футов.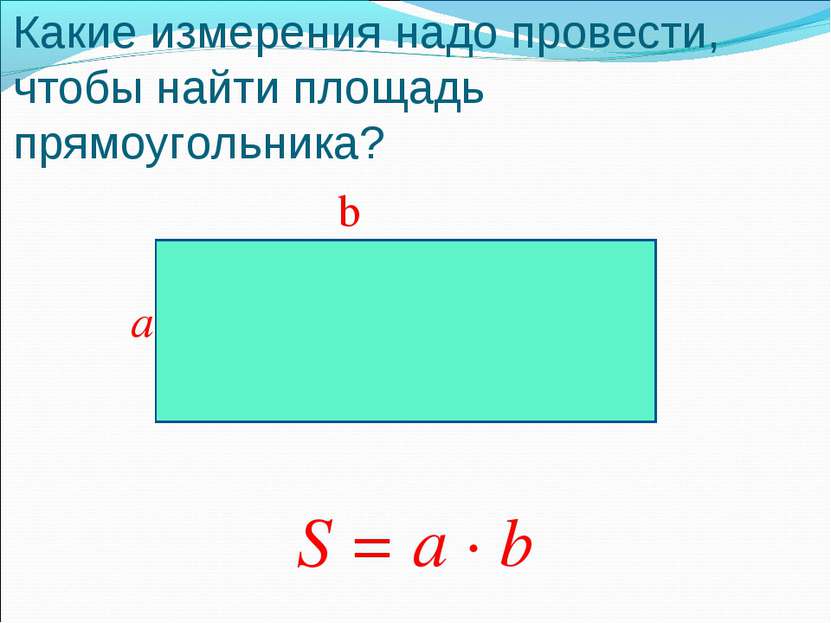 Формула утверждает, что $A=l\times w$, поэтому площадь двора равна $30\text{футов}\times25\text{футов}$, что составляет 750 квадратных футов. В этом случае 645 квадратных футов дерна недостаточно, чтобы покрыть весь двор. Потребуется еще 105 квадратных футов дерна.
Многие задачи на площади будут представлены в формате $A=l\times w$, где указаны длина и ширина и решается площадь. Тем не менее, также часто в задачах площади указывается площадь, но отсутствуют размеры. Например, площадь следующего прямоугольника равна 12 см ², а его длина равна 6 см. Какова ширина прямоугольника?
Формула площади может быть применена в подобных ситуациях, но формула должна быть изменена, чтобы найти 92=6\text{ см}\times w\), и чтобы найти w , нам нужно разделить обе части уравнения на 6. $w=2\text{ см}$, поэтому ширина прямоугольника 2 см.
Учтите следующее:
Вы хотите установить проволочный забор, окружающий ваш сад, чтобы отпугнуть оленей и кроликов.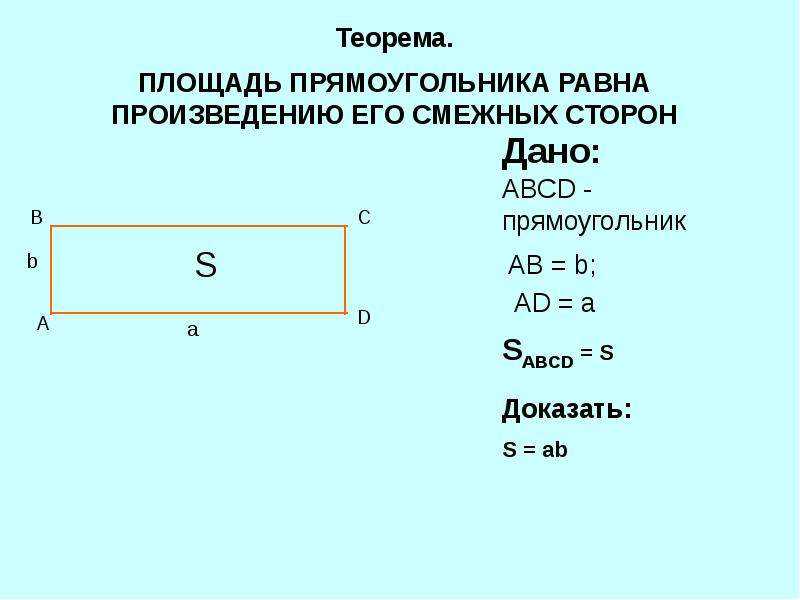 2=l14\text{ футов}\), и когда обе части уравнения делятся на 14, длина оказывается равной 15 футам. Отсюда мы можем просто сложить две длины и две ширины, чтобы найти общее количество необходимых ограждений: $14+14+15+15=58\text{футов ограждения}$. 92\).
Примеры вопросов по площади прямоугольника Вот несколько примеров вопросов по площади прямоугольника.
Вопрос №1:

Прямоугольник ниже имеет длину 4 дюйма и ширину 3 дюйма. Вычислите площадь поверхности по формуле площади.
15 в ²
11 в ²
14 в ²
12 в
09 2
0 Показать ответ0005 Ответ:
Площадь можно рассчитать по формуле $A=l\×w$, где A представляет площадь, l представляет длину, а w
представляет ширину. Формула $A=l\times w$ становится $A=4\text{in}\times3\text{in}$, что упрощается до 12 в ² .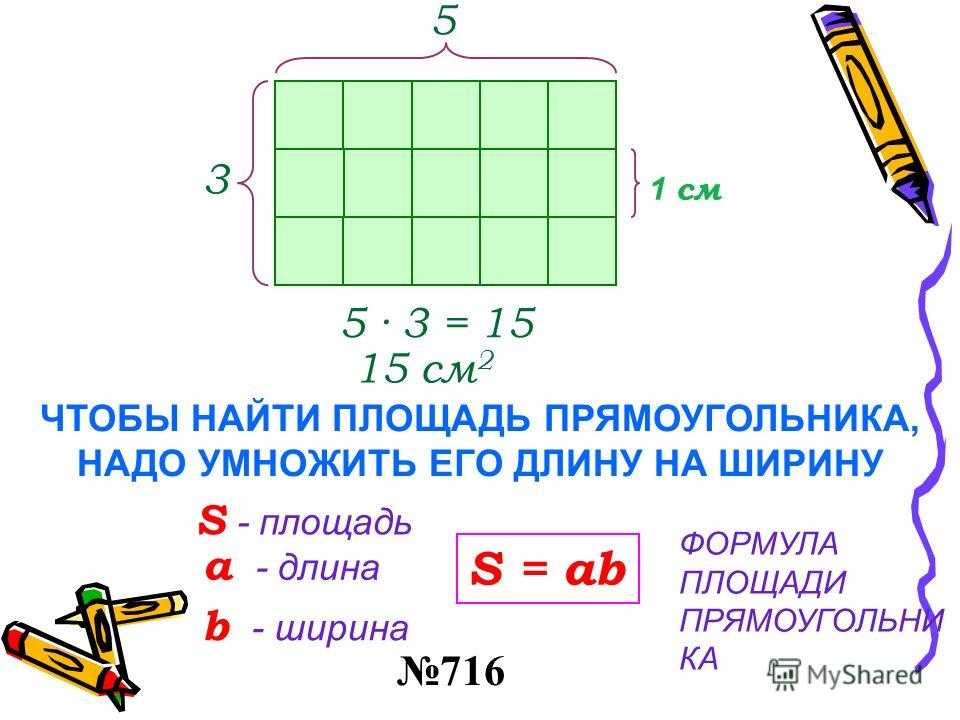
Скрыть ответ
Вопрос № 2:

Какой сценарий является примером площади поверхности?
Количество воды, содержащейся в большом баке
Вес объекта, измеренный в граммах
Расстояние вокруг беговой дорожки в метрах
Площадь плитки, покрывающей пол кухни
Показать ответ
Ответ:
Площадь поверхности может быть использована для описания ситуации, например, сколько плитки необходимо, чтобы полностью покрыть поверхность кухонного пола.
Скрыть ответ
Вопрос №3:

Сколькими способами можно построить прямоугольник, чтобы получить площадь поверхности 12 квадратных дюймов?
В одну сторону
В две стороны
Восемь сторон
В шесть сторон
Показать ответ
Ответ:
Следующие размеры дадут площадь поверхности 12 квадратных единиц (5 в \ text: 902} \times1\text{in}\)
$1\text{in}\times12\text{in}$
$2\text{in}\times6\text{in}$
$6\ текст {in}\times2\text{in}$
$3\text{in}\times4\text{in}$
$4\text{in}\times3\text{in}$
Скрыть Ответ
Вопрос № 4:

Кристен хочет вставить поролоновую прокладку в основание спального ящика своей собаки.
Ящик имеет длину 54 дюйма и ширину 36 дюймов. Какова должна быть площадь пенопластовой прокладки, чтобы без зазоров поместиться в ящик?
1 844 в ²
1,744 в ²
1 944 в ²
1,344 в ²
Show. вычисляется по формуле площади $A=l\times w$. Когда размеры подставлены в формулу, $A=l\times w$ становится $A=54\text{in}\times36\text{in}$, что упрощается до 1,944 в ² .
Скрыть ответ
Вопрос №5:

Эндрю хочет построить бассейн на заднем дворе. Его двор имеет ширину 15 футов, поэтому он решает спроектировать бассейн шириной 10 футов. Площадь бассейна составит 120 квадратных метров. Как долго будет бассейн?
11 футов
12 футов
13 футов
14 футов
Показать ответ
Ответ:
В этом сценарии формула \(A=l) может быть использована для решения \(A)times\ на недостающую длину стороны.}}