Формулы площади треугольника
Формулы площади треугольника
Подождите пару секунд пока подгрузятся формулы
Внимание! Десятичную дробь надо писать с точкой(.), а не с запятой!
Через основание и высоту
$$S= \frac{1}{2} ah $$
\(S\) — площадь треугольника\(a\) — основание
\(h\) — высота
\(a =\) \(h =\)
Через две стороны и угол
$$S= \frac{1}{2} ab sin \alpha $$
\(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\( \alpha \) — угол между сторонами \(a\) и \(b\)
\(a =\) \(b =\) \( \alpha =\)
Формула Герона
$$S= \sqrt{p(p-a)(p-b)(p-c)} $$
\(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(a =\) \(b =\) \(c =\)
Через радиус вписанной окружности
$$S= rp $$
\(S\) — площадь треугольника\(r\) — радиус вписанной окружности
\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(r =\) \(p =\)
Через радиус описанной окружности
\(S= \frac{abc}{4R} \)\(S\) — площадь треугольника
\(R\) — радиус описанной окружности
\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(a =\) \(b =\)
\(c =\) \(R =\)
Площадь прямоугольного треугольника
$$S= \frac{1}{2} ab $$
\(S\) — площадь треугольника \(a\) — сторона\(b\) — сторона
\(a =\) \(b =\)
Площадь прямоугольного треугольника
$$S= de $$
\(S\) — площадь треугольника\(d =\) \(e =\)
Формула Герона для прямоугольного треугольника
$$ S= (p-a)(p-b) $$
\(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(a =\) \(b =\) \(p =\)
Площадь равнобедренного треугольника
$$S= \frac{1}{2} a^2 sin \alpha$$
\(S\) — площадь треугольника\(a\) — сторона
\(\alpha\) — угол между боковыми сторонами
\(a =\) \( \alpha =\)
Площадь равнобедренного треугольника
\(a\) — сторона
\(b\) — сторона
\(\alpha\) — угол между боковыми сторонами и основанием
\(a =\) \(b =\) \( \alpha =\)
Площадь равнобедренного треугольника
$$S= \frac{b^2}{4tg \frac{ \alpha }{2}} $$
\(S\) — площадь треугольника\(b\) — сторона
\(\alpha\) — угол между боковыми сторонами и основанием
\(b =\) \(\alpha =\)
Формула Герона для равнобедренного треугольника
a = b =Площадь равностороннего треугольника
$$S= \frac{ \sqrt{3}a^2}{4} $$
\(S\) — площадь треугольника\(a\) — сторона
\(a =\)
Площадь равностороннего треугольника
$$S= \frac{3 \sqrt{3}R^2}{4}$$
\(S\) — площадь треугольника\(R\) — радиус описанной окружности
\(R =\)
Площадь равностороннего треугольника
$$S= 3 \sqrt{3}r^2 $$
\(S\) — площадь треугольника\(r\) — радиус вписанной окружности
\(r =\)
Площадь равностороннего треугольника
$$S= \frac{h^2}{\sqrt{3}}$$
\(S\) — площадь треугольника\(h\) — высота
\(h =\)
www.100formul.ru
Калькулятор расчета площади треугольного помещения
При расчете площадей помещений или других поверхностей, подлежащих отделке, порой приходится сталкиваться с многоугольными фигурами, которые неопытного человека могут поставить в тупик. Но на самом деле – нет ничего сложного, существует простой и точный способ провести необходимые вычисления.
Калькулятор расчета площади треугольного помещенияЛюбой многоугольник можно одной или несколькими линиями разбить на определенное количество треугольников, затем просчитать площади этих участков и просуммировать. А чтобы вычисления были произведены быстро и точно, примените предлагаемый калькулятор расчета площади треугольного помещения.
Несколько пояснений по работе с ним будут даны ниже.
Калькулятор расчета площади треугольного помещения
Перейти к расчётам
Несколько необходимых пояснений
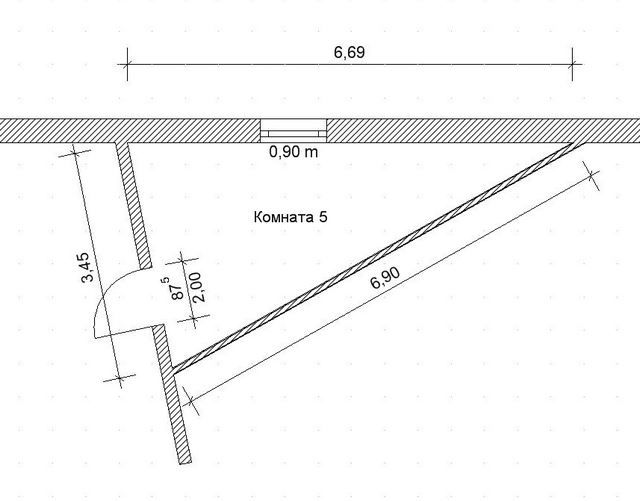
Треугольные помещения встречаются нечасто, но калькулятор может быть полезен и в иных случаях. Как уже говорилось, на треугольники несложно разбить любую многоугольную плоскую фигуру.
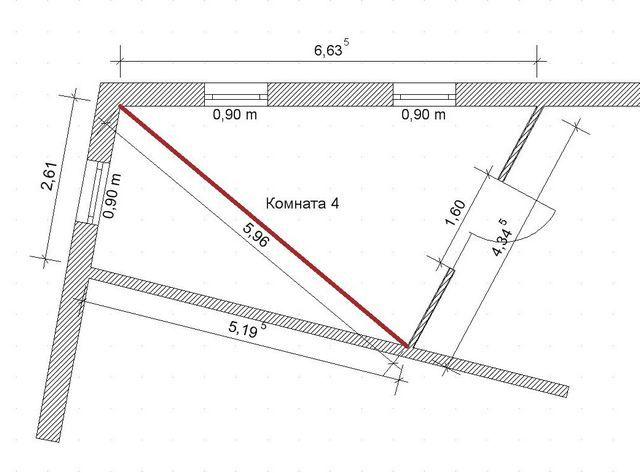Пример разбивки неправильного четырёхугольника на два треугольникаПлощадь треугольника чаще определяют произведением основания на высоты с последующим делением на два. Однако, в условиях стройки или ремонта пробить перпендикуляр, чтобы точно измерить высоту фигуры – не всегда бывает просто, если нет специальных инструментов. Даже небольшая ошибка в разметке способна привести к искажению конечного результата. Поэтому в данном случае применена формула Герона, позволяющая рассчитать площадь абсолютно любого треугольника по длинам трех его сторон, измерить которые – уже труда никакого не составит.
Значения запрашиваются в сантиметрах. Конечный результат – в квадратных метрах.
Если необходимо определит площадь прямоугольного или трапециевидного помещения, то есть у которого хотя бы одна пара сторон – параллельны друг другу, то для этого проще применить специальный калькулятор для четырехугольника. Он, кстати, учитывает возможное наличие выступов, колонн, ниш и других элементов, увеличивающих или уменьшающих общую площадь комнаты.
Существуют и более сложные случаи расчета площадей
Иногда приходится прибегать и к более сложным расчетам, когда некоторым стенам или элементам конструкции придана криволинейная форма. Как вычислить площадь комнаты при таких условиях – рассказывается в специальной публикации нашего портала.
Существуют и более сложные случаи расчета площадейПлощадь равнобедренного треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Проще всего найти площадь равнобедренного треугольника через высоту и основание. Высота делит такой треугольник пополам,
и используя формулу для нахождения площади прямоугольного треугольника, получаем, что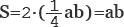 
, а в нашем случае 
Используя эту же формулу, можем найти площадь равнобедренного треугольника через стороны и основание. Для этого проведем в треугольнике высоту и воспользуемся теоремой Пифагора. Получим выражение 
. Отсюда 
, и соответственно 
, подставив полученное выражение вместо 
. Найти площадь равнобедренного треугольника, зная сторону и угол при вершине (между одинаковыми сторонами), можно используя аналогичную формулу для обычного треугольника, в котором известны две стороны: 
. Если известен угол при основании, то формула будет выглядеть по-другому – 
Зная основание и угол равнобедренного треугольника, нужно найти его высоту, тогда станет возможным рассчитать площадь. Из прямоугольного треугольника, который образует высота: 
. Тогда площадь будет равна: 
geleot.ru
Калькулятор расчета площади треугольного помещения
Как часто домашний мастер при производстве ремонта сталкивается с необходимостью вычисления площади того или иного помещения? Никаких сложностей не возникает, если комната имеет ровные стены и форму квадрата или прямоугольника. Но что делать, если она треугольная или же все ее стены имеют различную ширину? Тогда случае поможет калькулятор расчета площади треугольного помещения. Разберемся как он работает.
Комната может быть подобной формыЧитайте в статье
Калькулятор расчета площади треугольного помещения
Как работать с онлайн-калькулятором
На самом деле все достаточно просто. Начнем с комнаты треугольной формы. В соответствующие поля программы вносим длины всех стен по очереди. На этом, собственно, вся работа заканчивается. Остается лишь нажать на кнопку «Рассчитать», после чего появится результат, выраженный в квадратных метрах.
Нюансы вычислений в комнатах с разными стенами
Здесь задача немного усложняется. Алгоритм действий разбивается на два этапа. Для начала делим комнату на 2 треугольника. После этих действий высчитываем при помощи онлайн-калькулятора параметры каждого из них и складываем. Таким же образом поступаем и с многоугольными помещениями – любое из них легко можно разбить на треугольники.
Любой многоугольник можно разбить так, чтобы можно было произвести необходимые вычисленияКонечно можно выполнить все вычисления и самостоятельно, но не факт, что провести меридианы в помещении удастся идеально ровно. А любое расхождение – это погрешность, которая совершенно не нужна в расчетах.
Если все же решено производить подобную работу самостоятельно, предлагаем просмотреть полезный видеоролик:
ПОНРАВИЛАСЬ СТАТЬЯ? Поддержите нас и поделитесь с друзьями
housechief.ru