Объем цилиндра по диаметру и высоте: Расчет объема цилиндра по диаметру и высоте в мм (мм3, см3, м3, л)

формула через диаметр и высоту

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение объема цилиндра: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.

  • Формула вычисления объема цилиндра
    • Через площадь основания и высоту
    • Через радиус основания и высоту
    • Через диаметр основания и высоту
  • Примеры задач

Формула вычисления объема цилиндра

Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

V = S ⋅ H

Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R2. Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R2 ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14.

Через диаметр основания и высоту

Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:

V = π ⋅ (d/2)2 ⋅ H

Примеры задач

Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см2, а также, высота – 10 см.

Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см2 ⋅ 10 см = 785 см3.

Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.

Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см)2 ⋅ 6 см = 301,44 см3.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Калькулятор для цилиндра — intmag24.

ru Опубликовано от Admin — Оставить комментарий

Онлайн калькулятор для цилиндра позволяет по известным данным вычислить:

  • объем цилиндра,
  • площадь основания, площадь боковой поверхности и  площадь полной поверхности цилиндра,
  • элементы: радиус, диаметр и высоту.

 

Калькулятор для цилиндра: комментарий

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра).

Обозначения для цилиндра:
R – радиус, D – диаметр,
V – объем,
Sо – площадь основания, Sб – площадь боковой поверхности, S – площадь полной поверхности,
h – высота прямого кругового цилиндра (h2 и h3 — минимальная  и максимальная высота)
π – число Пи которое всегда примерно равно 3,14.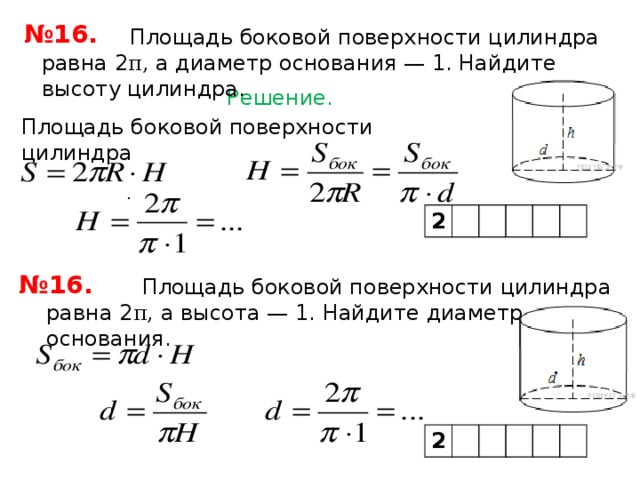

Прямой круговой цилиндр

Круговым называется цилиндр, если его направляющая является окружностью. Прямым называется цилиндр, если его образующая перпендикулярна основаниям.

Формулы для прямого кругового цилиндра:

Найти объем цилиндра, если известны:

  • радиус и высота цилиндра: V=πR2h
  • диаметр и высота цилиндра: V=πD2/4h
  • площадь и высота цилиндра: V=Sоh

Площадь(Sб) боковой поверхности прямого кругового цилиндра

Так как боковая поверхность представляет собой прямоугольник, то площадь боковой поверхности цилиндра определяется по формуле: Sб=2πR⋅h

Площадь(Sо) основания цилиндра

Основание цилиндра —круг, поэтому площадь одного основания находится по формуле площади круга: Sо=πR2.

Площадь(S)  полной поверхности прямого кругового цилиндра

Площадь полной поверхности цилиндра определяется по формуле: S=2πRh+2πR2=2πR(h+R)

Формулы нахождения радиуса и диаметра по:

  • высоте и объему: R=√(V/πh), D=2*√(V/πh)
  • площади боковой поверхности и высоте: R=Sб/2πh, D=2*Sб/2πh
  • площади основания и высоте: R=√(Sо/π), R=2*√(Sо/π)

Формулы нахождения высоты по:

  • радиусу и объему:
    h=V/πR2
  • площади боковой поверхности и радиусу: h=Sб/2πR
  • площади полной поверхности и радиусу: h=S/2πR-R

Скошенный цилиндр

Прямой круговой цилиндр со скошенным основанием (скошенный цилиндр) определяется радиусом основания R, минимальной высотой h2 и максимальной высотой h3.

Формулы для скошенного цилиндра:
  • Объем скошенного цилиндра: V=πR2(h2+h3)2
  • Площадь(Sб) боковой поверхности скошенного цилиндра: Sб=πR(h2+h3)
  • Площадь(Sо) оснований скошенного цилиндра: Sо=πR2+πR √(R2+((h2−h3)/2)2)
  • Площадь(S) полной поверхности скошенного цилиндра  
    S=Sб+Sо= πR(h2+h3)+ πR2+πR √ (R2+((h2−h3)/2)2)  = πR[(h2+h3)+ R+√ (R2+((h2−h3)/2)2) ]

 

Список всех онлайн-конвертеров на странице «Калькуляторы«.

Рубрика: Калькуляторы

Метки Математика, Геометрия

Объем цилиндров – объяснение и примеры

Объем цилиндра – это мера объема пространства, занимаемого цилиндром, или мера емкости цилиндра.

Эта статья покажет вам, как найти объем цилиндра, используя формулу объема цилиндра.

В геометрии цилиндр представляет собой трехмерную форму с двумя равными и параллельными окружностями, соединенными изогнутой поверхностью.

Расстояние между круглыми гранями цилиндра называется высота цилиндра . Верх и низ цилиндра представляют собой две конгруэнтные окружности, радиус или диаметр которых обозначаются как « r » и « d » соответственно.

Чтобы рассчитать объем цилиндра, вам нужен радиус или диаметр круглого основания или вершины и высота цилиндра.

Объем цилиндра равен произведению площади круглого основания на высоту цилиндра. Объем цилиндра измеряется в кубических единицах.

Расчет объема цилиндра полезен при проектировании цилиндрических объектов, таких как:

  • Цилиндрические резервуары для водного водного водного водного водяного. химические лаборатории

Формула объема цилиндра

Формула объема цилиндра дается как:

Объем цилиндра = πr 2 h кубических единиц

Где πr 2 = площадь круга;

π = 3,14;

r = радиус круглого основания и;

h = высота цилиндра.

Для пологого цилиндра объемная формула задается как:

Объем цилиндра = πh (R 1 2 — R 2 2 )

Где, r 1 =

. внешний радиус и r 2 = внутренний радиус цилиндра.

Разность внешнего и внутреннего радиусов образует толщину стенки цилиндра, т.е.

Толщина стенки цилиндра = r 1 – r 2

Решим несколько примеров задач на объем цилиндров.

Пример 1

Диаметр и высота цилиндра 28 см и 10 см соответственно. Каков объем цилиндра?

Решение

Дано;

Радиус равен половине диаметра.

Диаметр = 28 см ⇒ радиус = 28/2

= 14 см

Высота = 10 см

По формуле объема цилиндра;

Том = πr 2 H

= 3,14 x 14 x 14 x 10

= 6154,4 см 3

Со. Объем цилиндра 6154,4 3

Пример 2 3

Пример 2 444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444443930444393043 4003

Глубина воды в цилиндрическом резервуаре составляет 8 футов. Предположим, что радиус и высота резервуара равны 5 футам и 11,5 футам соответственно. Найдите объем воды, необходимый для заполнения бака до краев.

Раствор

Сначала рассчитайте объем цилиндрического резервуара

Объем = 3,14 x 5 x 5 x 11,5

= 902,75 куб. = 628 кубических футов.

Объем воды, необходимый для заполнения бака = 902,75 – 628 кубических футов

= 274,75 кубических футов.

Пример 3

Объем цилиндра 440 м 3 , радиус основания 2 м. Рассчитайте высоту бака.

Решение

Объем цилиндра = πr 2 H

440 M 3 = 3,14 x 2 x 2 x H

440 = 12,56H

, разделяя 12.56 на обоих сторонах, We Get

9

2

2

2

2

. h = 35

Следовательно, высота резервуара 35 метров.

Пример 4

Радиус и высота цилиндрического резервуара для воды равны 10 см и 14 см соответственно. Найдите объем бака в литрах.

Решение

Объем цилиндра = πr 2 H

= 3,14 x 10 x 10 x 14

= 4396 см 3

, 1 литр = 1000 кубический сантиметр (CM 3 )

5.

Следовательно, разделите 4396 на 1000, чтобы получить

Объем = 4,396 литра

Пример 5

Внешний радиус пластиковой трубы равен 240 мм, а внутренний радиус равен 200 мм. Если длина трубы 100 мм, найдите объем материала, из которого изготовлена ​​труба.

Решение

Труба является примером полого цилиндра, поэтому мы имеем

объем цилиндра = πh (R 1 2 — R 2 2 )

= 3,1468 2 2 ). 100 x (240 2 – 200 2 )

= 3,14 x 100 x 17600

= 5,5264 x 10 6 мм 3 мм

Пример 6

Цельный цилиндрический блок металла необходимо расплавить, чтобы сформировать кубы с ребром 20 мм.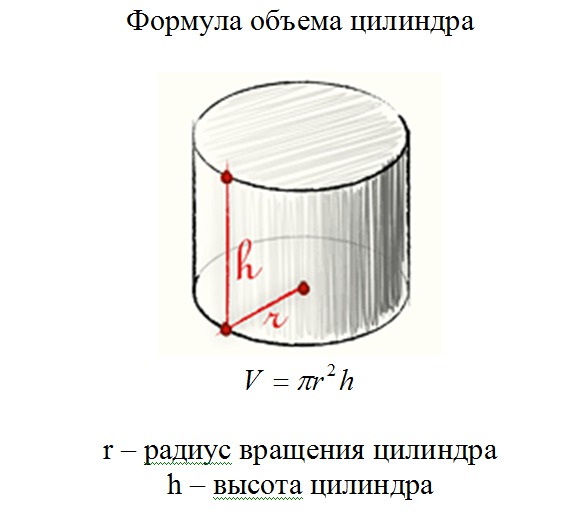 Предположим, что радиус и длина цилиндрического блока равны 100 мм и 49 мм.0 мм соответственно. Найдите количество кубиков, которые нужно составить.

Решение

Рассчитайте объем цилиндрического блока

Объем = 3,14 x 100 x 100 x 490

= 1,5386 x 10 7 мм 3

Объем куба = 20 x 20.

= 8000 мм 3

Количество кубов = объем цилиндрического блока/объем куба

= 1,5386 x 10 7 мм 3 / 8000 мм 39500051

= 1923 куба.

Пример 7

Найдите радиус цилиндра с той же высотой и объемом, что и у куба со стороной 4 фута. футов и,

объем куба = объем цилиндра

4 x 4 x 4 = 64 кубических фута

Но объем цилиндра = πr 2 ч

3,14 x r 2 x 4 = 64 кубических фута

12,56r 2 = 64

Разделите обе стороны на 12,56

r 2 = 5,1 фута.

r = 1,72

Следовательно, радиус цилиндра будет 1,72 фута.

Пример 8

Сплошная шестиугольная призма имеет длину основания 5 см и высоту 12 см. Найдите высоту цилиндра такого же объема, что и призма. Возьмем радиус цилиндра равным 5 см.

Раствор

Формула объема призмы дается как;

Объем призмы = (h)(n) (s 2 )/ [4 tan (180/n)]

где n = количество сторон

s = длина основания призмы

h = высота призмы

Объем = (12) (6) (5 2 )/ (4tan 180/6)

=1800/2,3094

=779,42 см 3

Объем цилиндра 2 ч

779,42 = 3,14 х 5 х 5 х ч

ч = 9,93 см.

Значит, высота цилиндра будет 9,93 см.

 

Объем цилиндра: определение, формула, примеры

Сталкиваетесь ли вы с трудностями при нахождении объема цилиндра, если его форма искажена? Задумывались ли вы над тем, как найти объем таких цилиндров? Это то, что вы узнаете через мгновение.

Объем цилиндра означает пространство внутри цилиндра, которое может вместить определенное количество материала. Проще говоря, способность цилиндра удерживать предмет — это его объем. Внутри пространства цилиндра вы можете удерживать любой из трех типов материи — твердое, жидкое или газообразное. Эту емкость можно наблюдать только в трехмерном цилиндре, т. е. вы не можете удержать ни жидкость, ни твердое тело, ни газ в двумерном цилиндре.

Совершенный трехмерный цилиндр имеет два конгруэнтных и параллельных одинаковых основания. Это известно как правильный круговой цилиндр. В прямом круговом цилиндре основания круглые, а каждый отрезок является частью боковой криволинейной поверхности, перпендикулярной основаниям. Вы могли видеть правильные круглые цилиндры в своей повседневной жизни. Формы банок, формы рулонов бумаги, прямое стекло и многое другое.

Однако, если форма стакана совершенно прямая, он будет называться правильным круглым цилиндром. Если форма нелинейна, то какой она будет?

Если две конгруэнтные и идентичные параллельные стороны каким-то образом станут непараллельными или деформируются, вы получите один из следующих цилиндров:

  1. Наклонный цилиндр — это цилиндр, стороны которого наклонены к основанию под углом, не равным равен прямому углу. Это будет форма искаженного стекла, о которой говорилось выше.
  2. Эллиптический цилиндр – это цилиндр, основания которого представляют собой эллипсы.
  3. Прямой круглый полый цилиндр – имеет форму правильного круглого цилиндра. Однако в конце нет замкнутых кругов.

Найти объем цилиндра проще, чем вы думали. Если вам все еще интересно, как найти объем цилиндра, все, что вам нужно, это ведро с водой, весы и пустая плоская поверхность, на которую можно поставить ведро.

Поставьте ванну на плоскую пустую поверхность и начните наполнять ее водой. Вы должны убедиться, что вода заполнена до краев. Как только ванна наполнится водой, поместите цилиндр, объем которого вам нужно найти, внутрь ванны. Вы увидите, как вода начнет выходить из ванны.

Соберите выпавшую воду в стакан. Убедитесь, что вода не падает, пока вы делаете преобразование. Поставьте стакан на весы и запишите вес воды. Не забудьте вычесть вес стакана. Вы должны иметь только вес воды.

Согласно закону Архимеда, вес воды, падающей из ванны, будет равен весу цилиндра. Следовательно, вес полученной воды будет равен весу цилиндра. Вам может быть интересно, как найти объем цилиндра?

Согласно физике, если вы находитесь в помещении с комнатной температурой, вес будет равен объему. Это означает, что 1 кг будет эквивалентен 1 литру и так далее. Следовательно, вы получите объем цилиндра из объема воды.

Но что, если вы живете в холодном или жарком регионе? Тогда вам придется использовать другой метод.

Формула для нахождения объема цилиндра

Вы можете найти объем цилиндра, используя формулу. Это универсально и может применяться независимо от вашего региона. Единицами объема являются кубические сантиметры, кубические дюймы или любые стандартные единицы с префиксом «кубический».

Объем цилиндра можно найти двумя способами. Вот они:

  1. Используя площадь и высоту
  2. Используя размеры
  • Нахождение объема цилиндров по площади и высоте есть не что иное, как произведение площади и высоты любой формы. Это правило справедливо для всех трехмерных фигур, известных в математике. Например, в кубоиде, если вы знаете площадь одной его стороны, а затем умножаете ее на высоту или ширину, то есть на оставшуюся сторону, вы получите объем.

В цилиндрах V = площадь x высота 

  • Нахождение площади с известными размерами – Универсальная формула для нахождения объема цилиндра: π r 2 ч, где значение π (пи) равно 3,14. или 22/7, r — радиус верха или низа цилиндра, а h — высота. Используя формулу, можно найти объемы прямых круговых цилиндров и косых цилиндров.

Однако для эллиптических цилиндров формула другая. Поскольку эллиптические цилиндры имеют разные радиусы, формула для нахождения их объемов имеет вид: V = π abh, где π = 22/7 или 3,14, a и b — радиусы основания эллиптического цилиндра, а h — высота .

Кроме того, формула также отличается для полых прямоугольных цилиндров. Объем полого прямоугольного цилиндра определяется формулой: V = π (R 2 – r 2 ) h, где R – внешний радиус круглого основания, r – внутренний радиус, а h – высота цилиндра.

Если вы ищете формулу площади поверхности цилиндра, то вот она: A = 2πr 2  + 2πrh, где r и h — радиус и высота цилиндра соответственно. Единицами площади поверхности будут квадратные единицы.

Шаги для расчета объема цилиндра

Следуя приведенным ниже методам, вы можете найти объем цилиндра.

Шаг 1: Определите тип цилиндра, данный вам в вопросе или в реальной жизни.

Шаг 2: Когда у вас есть тип цилиндра, вам нужно выяснить формулу, по которой можно найти объем цилиндра.

Шаг 3: Теперь у вас есть и формула. Проверьте, какие размеры вам нужны, чтобы найти объем. Убедитесь, что все размеры имеют одинаковые единицы измерения.

Шаг 4: Расставьте их по своим местам и рассчитайте объем.

Шаг 5: Сохраните единицы измерения после расчетного значения как «кубические единицы». Используйте соответствующую единицу измерения, такую ​​как метр, сантиметр или любую другую, вместо слова единица измерения.

Примеры для нахождения объема цилиндра

Пример 1. Цилиндр имеет радиус 50 см и высоту 100 см. Как найти объем цилиндра?

Решение: Мы знаем, что объем цилиндра находится по формуле – π r 2 h, где r — радиус цилиндра, а h — высота.

Таким образом, подставляя значения, получаем

Пример 2: Как найти объем цилиндра, один из радиусов которого равен 40 см, а другой — 60 см? Цилиндр имеет высоту 200 см.

Решение: Из приведенных данных видно, что цилиндр эллиптический, так как радиусы разные. Чтобы найти объем эллиптического цилиндра, используется формула V = π abh, где a и b — радиусы, а h — высота.

Следовательно, объем цилиндра = V = π abh

= π x 40 x 60 x 200 = 1507200 см 3 .

Пример 3: Как найти объем полого цилиндра изнутри и имеет внешний и внутренний радиусы единиц 6 и 8 соответственно? Высота этого полого цилиндра составляет 15 единиц.

Решение: Мы знаем, что формула объема полого цилиндра имеет вид V = π (R 2 – r 2 ) h.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *