Рассчитать емкость конденсатора онлайн: Расчёт ёмкости конденсатора онлайн / Калькулятор / Элек.ру

Расчет параметров конденсатора онлайн

Не знаю как Вам, а мне никогда не нравилось работать и вычислять ёмкости конденсаторов. Больше всего раздражало  наличие в исходных  данных, ёмкостей в разных номиналах, в пикофарадах, в нанофарадах, микрофарадах.  Их приходилось переводить в Фарады,  что влекло за собой глупейшие ошибки в расчетах.

Конденсатор — в принципе это любая конструкция, которая может сохранять накопленный электрический потенциал.  Если же эта конструкция, не только хранит электроэнергию, но и генерирует её, то это уже источник электропитания и никак  не конденсатор.

Конструкция конденсаторов может быть любой, но чаще всего в практике используется плоский конденсатор, состоящий из двух проводящих пластин, между которыми находится какой либо диэлектрик.  Это связано с тем, что расчет ёмкости такого конденсатора ведется по известной формуле и простотой его создания. Свернув такой плоский конденсатор в рулон, мы получаем, что при фактическом скромном размере  «рулона», там находится плоский конденсатор, длиной в десятки сантиметров и обладающий повышенной ёмкостью.

Емкости конденсаторов некоторых форм известны, и мы дальше их рассмотрим.

Но хотелось бы заметить, что на наш взгляд, потенциал  развития  конденсаторов до  конца не завершен. Ведь форма конструкции какого либо конденсатора может быть любая, материалы из которого сделаны обкладки или диэлектрический слой  тоже могут быть любыми в пределах таблицы Менделеева. Единственная сложность, это невозможность теоретически просчитать потенциальную ёмкость, новосозданного (другой конструкции) конденсатора. Это усложняет нахождение самой лучшей конструкции конденсатора.

Есть хорошая книга по рассмотрению электрической ёмкости различных фигур. Для любопытных рекомендую поискать на просторах Интернета: Расчет электрической ёмкости в авторстве Ю.Я.Иоселль 1981 года

Данный бот рассчитывает параметры типовых форм конденсаторов. Отличие от других калькуляторов, присутствующих в интернете, это возможность задавать параметры, которые Вам известны, для того что бы рассчитать остальные.

И последнее нововведение, которое вы можете использовать. Вам не обязательно придется переводить заданные данные в  метры, фарады и т.д. Достаточно обозначить размерность данных. 

Например, если ёмкость известна и равно 100 пикофарад, то боту можно так и написать c=100пикофарад или с=100пФ, бот сам  переведет в Фарады.

Результат, тоже будет выдан оптимально визуальному восприятию пользователя. 

Это стало возможно с созданием бота Система единиц измерения онлайн

Плоский конденсатор. Параметры

Полученные характеристики плоского конденсатора

Самая простая и самая распространенная конструкция конденсатора это два плоских проводника разделенных тонким слоем диэлектрика ( то есть материала не проводящего электрический ток).

 

Ёмкость такого сооружения определяется следующей формулой.

 

где ε0 = 8,85.10-12 Ф/м — абсолютная диэлектрическая проницаемость

Если же конденсатор состоит не из пары пластин, а каого то n-ого количества плоских пластин то ёмкость такого «слоёного» конденсатора составит

Еще интереснее выглядит формуа такого «слоёного» конденсатора,  если в слоях находятся разные диэлектрики , разной толщины d

 

S- площадь одной из обкладок конденсатора ( предполагаем что другая обкладка имеет такую же площадь)

d- расстояние между обкладками

С- ёмкость конденсатора

Рассмотрим примеры

Задача: Ёмкость плоского конденсатора 350 нанофарад, расстояние между обкладками 1 миллиметр, и заполнено воздухом. Определить какова площадь обкладок?

Сообщаем боту что нам известно: C=350нФ, d=1мм. Так как у воздуха диэлектрическая проницаемость 1.00059 то e=1.00059. Поле площадь очистим, так именно его мы будем определять

Получаем  вот такой ответ

Полученные характеристики плоского конденсатора

d = 1 милиметр  e = 1.00059  C = 350 нанофарад  S = 39.524703024086 м2

 

Ответ, площадь обкладок конденсатора при таких значениях должна составлять почти 40 квадратных метров.

Цилиндрический  КОНДЕНСАТОР

     

Полученные характеристики цилиндрического конденсатора

Цилиндрический конденсатор представляет в простейшем случае две трубки разного диаметра вложенных друг в друга. разделенных диэлетриком

 

Иногда может получится так, что ёмкость цилиндрического конденсатора станет отрицательной величиной. Ничего страшного, это лишь говорит о том что Вы перепутали радиусы внешней и внутренней оболочки местами.

 

• Расчет понижающего конденсатора >>

Онлайн калькулятор расчета запасаемой энергии в конденсаторе

Конструктивно конденсатор представляет собой емкостной элемент, состоящий из двух параллельно расположенных пластин, пространство между которыми заполнено диэлектриком.

Устройство конденсатора

Принцип работы конденсатора заключается в способности накапливать определенную величину заряда на пластинах и отдавать их обратно в сеть при прохождении через него переменного тока. Для цепи постоянного тока конденсатор представляет собой разрыв, но пластины все равно способны накапливать заряд. Основным параметром конденсатора является емкость, выражающаяся в Фарадах и способность накапливать заряд, выражаемая величиной энергии в Джоулях.

Если емкость конденсатора указывается на корпусе элемента и является его паспортным значением, то количество запасаемой энергии можно определить путем вычислений. Наиболее простым способом вычисления является использования онлайн калькулятора.

Для этого выполните такую последовательность действий:

• Внесите в первую графу калькулятора значение напряжения на конденсаторе в Вольтах;
• Укажите во втором поле величину емкости элемента в микрофарадах;
• Внесите значения сопротивления конденсатора и нажмите кнопку «Рассчитать».

В результате онлайн калькулятор расчета запасаемой энергии в конденсаторе выдаст значение заряда и времени, расходуемого на полный заряд емкостного элемента, подключенного к цепи.

Расчет величины заряда, накапливаемого в конденсаторе, и времени, необходимого для накопления этого заряда производится по таким формулам:

Где,

• W – это количество запасаемой энергии в конденсаторе;
• U – величина напряжения, приложенного к конденсатору;
• C – емкость конденсатора.

Для определения времени, затрачиваемого на накопление этого количества запасаемой энергии, в калькуляторе используется формула: T_зар = R*C

Где

• T_зар  — период времени, необходимый для накопления заряда, зависящий от параметров элемента;
• R – величина омического сопротивления конденсатора;
• C – емкость конденсатора.

 

Онлайн калькулятор расчета последовательного соединения конденсаторов

Физически, каждый из конденсаторов является разрывом в цепи, который накапливает и передает заряд за счет подачи на него переменного напряжения. Последовательное соединение конденсаторов подразумевает под собой подключение конца одного емкостного элемента к началу второго. Поэтому при последовательном включении через все конденсаторы протекает один ток, который зависит от их емкости и частоты напряжения в сети. В электротехнике такой тип подключения элементов нашел широкое применение в радиоэлектронике современных компьютеров, радиостанций и прочих устройств.

Рис. 1. Последовательное соединение конденсаторов

 

Как видите на рисунке 1, в нормальном режиме работы системы через все конденсаторы происходит передача электроэнергии, но в случае перегорания какого-либо емкостного элемента или сразу нескольких прекращается электроснабжение всех деталей. Для замены такого элемента в цепи необходимо установить другой конденсатор или заменить его на несколько. При отсутствии элемента нужной емкости вам пригодиться такой способ для перерасчета.

Формула для подсчета суммарной емкости последовательно соединенных конденсаторов выглядит таким образом:

Где, С₀ — общая емкость последовательно соединенных конденсаторов

С₁ — емкость первого конденсатора;

С₂ — емкость второго конденсатора;

С_n — емкость n-ого конденсатора в цепи.

Как видите, процесс расчета потребует от вас длительных и кропотливых операций, поэтому гораздо проще воспользоваться онлайн калькулятором для вычисления суммарной емкости последовательно соединенных конденсаторов.

Онлайн калькулятор расчета параллельного соединения конденсаторов

В устройствах радиоэлектроники конденсаторы представляют собой один из важнейших элементов, способный накапливать и отдавать электрический заряд. В сравнении с другими элементами, конденсатор обладает такими параметрами как емкость и сопротивление. Сопротивление конденсатора обусловлено изолирующим промежутком, который может выйти со строя из-за скачков напряжения или других аварийных процессов в сети. При необходимости заменить какой-либо конденсатор, многие радиолюбители сталкиваются с трудностью достать модель нужной емкости.

В таком случае на помощь придет правило сложения, позволяющее заменить одно устройство несколькими меньшей емкости, чтобы в суме их хватило для компенсации вышедшего со строя конденсатора. В этом месте многие не могут определить, каким способом вычисляется суммарная мощность параллельно соединенных конденсаторов. Следует отметить, что физически для схемы конденсатор представляет собой разрыв.

Рис. 1. Параллельное соединение конденсаторов

Посмотрите на рисунок 1, это принципиальная схема параллельного подключения конденсаторов. Как видите, в этом случае одноименные выводы емкостного элемента подводятся к соответствующей точке электрической цепи. Поэтому и емкость между плоскостями двух  и более конденсаторов, соединенных между собой параллельно складывается в одно целое. Исходя из этого, суммарная емкость для параллельно включенных конденсаторов будет вычисляться по формуле:

С₀ = С₁ + С₂ + … + С_n

Где,

• С₀ — общая емкость параллельно соединенных конденсаторов
• С₁ — емкость первого конденсатора;
• С₂ — емкость второго конденсатора.

В данном примере рассматривается ситуация, когда параллельно соединяются только два емкостных элемента, поэтому их результирующая емкость будет равна арифметической сумме емкостей обоих конденсаторов. На практике можно применять и большее число, если вам необходимо получить определенную емкость.

Чтобы рассчитать результирующую емкость при параллельном соединении 2 и более конденсаторов вы можете воспользоваться нашим онлайн калькулятором ниже.

Программа для определения емкости конденсатора по цифровой маркировке

Данная программа позволяет оперативно определить емкость конденсатора по цифровой маркировке. Определение емкости конденсатора выполняется в соответствии со стандартами IEC по таблице 1. Сам принцип определения емкости конденсатора показан на рис.1.

Таблица 1

Рис.1 – Определение емкости конденсатора

Рассмотрим на примере определение емкости конденсатора по цифровой маркировке с помощью данной программы. Выберем конденсатор с цифровой маркировкой 104, для данного конденсатора в соответствии с таблицей 1 и представленным методом определения емкости (см.рис.1), емкость составит: 104 = 10 х 104 = 100000 pF = 100 nF = 0,1 µF, для цифровой маркировки 330, емкость составит: 330 = 33 pF = 0,033 nF = 0,000033 µF. Как мы видим, программа правильно определяет емкость конденсатора по цифровой маркировке.

Если же Вам нужно определить емкость конденсатора по цветовой маркировке, воспользуйтесь программой «Конденсатор v1.2».

конденсатор по цифровой маркировке, определить емкость конденсатора по цифровой маркировке, определить емкость по цифровой маркировке, программа определения емкости по цифровой маркировке

Поделиться в социальных сетях

Благодарность:

Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding».

Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.

Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.

Заряд и разряд конденсатора через сопротивление

Полученные характеристики ЗАРЯДА конденсатора через сопротивление

 

Заряд конденсатора емкостью от источника тока через наружное сопротивление происходит в соответствии с формулой

 

 

 

при этом мгновенный зарядный ток:

 

 

где — рассматриваемый момент времени в секундах от момента начала заряда; — напряжение на обкладках конденсатора момент времени t в Вольтах; — напряжение источника, от которого производится заряд конденсатора в Вольтах — емкость конденсатора в Фарадах — сопротивление последовательной цепи в Омах — постоянная времени в секундах ().

 

Разряд конденсатора емкостью , заряженного до разности потенциалов через сопротивление представляющее внешнее сопротивление разрядной цепи или внутреннее сопротивление утечки самого конденсатора происходит в соответствии с формулой

 

 

Мгновенная величина разрядного тока

 

 

где — напряжение между обкладками конденсатора через секунд после начала разряда,— ток в цепи (внешней или внутренней) конденсатора существующей через секунд после начала разряда.

 

Полученные характеристики РАЗРЯДА конденсатора через сопротивление

 

Процессы заряда и разряда конденсаторов рассматриваются обычно в зависимости от постоянной времени цепи . Постоянная времени практически указывает, через какой промежуток времени (в секундах) напряжение разряжаемого конденсатора уменьшается в раз,

от рассматриваемого напряжения. При заряде конденсатора постоянная времени указывает время (в секундах), в течение которого напряжение на обкладках повышается на 63% от разницы между имевшимся напряжением и напряжением источника тока заряда.

 

В связи с тем что заряд и разряд до полных значений конечных напряжений длятся неопределенно долгий срок, часто удобнее считать режим заряда законченным при доведении напряжения на обкладках до 99% от заряжающего напряжения (или до 1% от первоначальной величины напряжения при разряде).

 

Синтаксис

Для пользователей XMPP клиентов, используется команда

fiz ключи

где ключи это известные параметры, параметра=значение, разделенные точкой с запятой

Обязателен ключ key=razryad при расчете разаряда конденсатора

и zaryad  при расчете заряда

Так как при других параметрах ключах будут рассчитываться совершенно другие формулы. Например баллистического движения или давления над уровнем моря.

 

Заметьте, чем данный калькулятор  отличается от других:

Во первых: данные можно вводить не переводя из наноФарад в Фарады, а килоОмы в Омы. Если уж заданы параметры   в единицах измерения то так и пишите.  Если не напишите то считается  что данные заданы  в основным единицах СИ ( то есть метр, Фарад, Ом)

Во вторых: Расчет ведётся по тем  параметрым которые можно рассчитать зная исходные.Это очень удобно, когда нужно рассчитать любой из параметров в формуле, когда известны все остальные.  Другие известные калькуляторы могут рассчитывать только по определенному алгоритму  и только в одну сторону.

 

Примеры использования бота

Определим время заряда конденсатора ёмкостью 1микроФарад, до 5 Вольт, если сопротивление цепи 1 килоОм.

Напряжение внешнего источника питания 12 Вольт, а на обкладках конденсатора напряжение, в момент подключения источника питания, составляло 1 Вольт.

 

Что бы сразу хотелось бы заметить. Как видно из задачи у нас  есть остаточное напряжение на конденсаторе в размере 1 Вольт, которое надо учитывать в расчетах времени заряда.

Данные, которые мы будем вводить следующие:

U0=12-1 =11В

Ut=5-1=4В 

R=1кОм

С=1мкФ

 

пишем запрос fiz U0=11В;Ut=4В;R=1кОм;C=1мкФ;key=zaryad

и получаем ответ

U0 = 11 Вольт

Ut = 4 Вольт

R = 1 килоОм

C = 1 микрофарад

T = 1 милисекунда

tt = 0.4519851237 милисекунда

 

То есть решение = 451.98 мкс

 

Теперь давайте проверим наши расчеты. Если бы конденсатор был бы в момент подключения источника питания полностью разряжен

То при условии зарядки его до 1 Вольта наш запрос был бы таким

fiz U0=12В;Ut=1В;R=1кОм;C=1мкФ;key=zaryad

 

и время заряда было бы tt = 87.011377 микросекунда

 

а при зарядки до 5 Вольт был бы таким

 

fiz U0=12В;Ut=5В;R=1кОм;C=1мкФ;key=zaryad

 

и время заряда было бы tt = 538.9965007 микросекунда

 

То время заряда конденсатора  с 1В до 5 Вольт составило бы 538.9965007 микросекунда минус  87.011377 микросекунда = 451.98 мкс

 

Что несомненно говорит о правильности наших расчетов по изначальным условиям.

 

 

• Из звезды в треугольник. Эквивалентная схема. >>

Заряд и разряд конденсатора через сопротивление | 2014-06-23 10:12:35 | Варламов Дмитрий | Электротехника онлайн |

5 3 51

Расчет параметров заряда и разряда конденсатора через сопротивление онлайн. Определение всех необходимых параметров | заряд, конденсатор, разряд, время, онлайн

Расчёт блока питания с гасящим конденсатором + онлайн-калькулятор — radiohlam.ru

Осторожно, текст под спойлером перегружен физикой!

Итак, процессы в этой схеме будут достаточно нелинейны, поэтому при рассчётах придётся делать различные упрощения и допущения.

Для начала давайте будем считать, что ёмкость конденсатора C₂ достаточна для полного сглаживания пульсаций напряжения после моста, то есть напряжение на конденсаторе C₂ = const. Далее попробуем нарисовать пару графиков, — напряжение на входе моста (U_M) и ток через конденсатор C₁ (I_C1), опираясь на график сетевого напряжения U_С(t). Будем считать, что сетевое напряжение у нас изменяется по синусоидальному закону и имеет амплитуду Uca (вообще-то рисовать мы будем косинусоиду, нам так будет удобнее, но это по сути одно и то же, только косинусоида сдвинута относительно синусоиды на π/2).

Рассуждаем следующим образом: в каждый момент времени полное напряжение и полный ток в этой цепи можно описать следующими уравнениями:

U_C=U_C1+U_М (1), i_C=i_C1+i_М (2)

В момент времени t₀ уравнение напряжения примет вид: Uca=U_C1+U_М. Поскольку Uca — это максимальное значение сетевого напряжения, то U_C1 и U_М также в этот момент должны иметь максимальные значения (здесь в логике есть небольшой провал, максимум суммы — это не всегда сумма максимумов, функции могут быть сдвинуты по фазе, но… в общем, мы потом всё экспериментально проверим).

Максимальное значение U_М равно Uвых, поскольку если бы напряжение на мосту поднималось выше, то и конденсатор C₂ заряжался бы до большего напряжения (мост бы открылся и к конденсатору C₂ потёк бы зарядный ток, увеличивая напряжение на нём).

Токи через конденсатор и мост в момент t₀ равны нулю. Про мост я выше уже написал (если бы через него тек ток, то конденсатор C₂ заряжался бы дальше), а через C₁ ток не течёт, поскольку ток через конденсатор — это первая производная от напряжения, которая в точках экстремума обращается в ноль (значит когда напряжение на конденсаторе максимально — ток равен нулю).

Далее сетевое напряжение (U_C) начинает уменьшаться. При этом напряжение на C₁ не меняется (тока-то через мост нет, заряд на C₁ не меняется), следовательно вместе с падением U_C уменьшается напряжение на входе моста.

В момент, когда сетевое напряжение упадёт до значения Uca-2Uвых (момент времени t₁) — напряжение на входе моста достигнет значения -Uвых (находим с помощью формулы 1), диоды моста откроются и в первичной цепи (через мост и конденсатор C₁) потечёт ток. При этом напряжение на входе моста перестанет меняться (помните, мы договорились, что ёмкость C₂ достаточно большая для того, чтобы полностью сгладить пульсации).

Обратите внимание, что напряжение на входе моста в этот момент равно -Uм, так что ток потечёт в обратную сторону от того направления, в котором он тёк до момента времени t₀. Этот ток, поскольку он течёт в обратную сторону, начнёт перезаряжать конденсатор C₁.

К моменту времени t₃ напряжение в сети достигнет максимума, только с противоположной относительно момента t₀ полярностью. Соответственно, для этого момента экстремума сетевого напряжения будут справедливы все те же рассуждения касательно напряжений и токов, которые мы использовали для момента t₀. То есть, к этому моменту конденсатор C₁ полностью перезарядится (напряжение на нём достигнет максимального значения отрицательной полярности), а ток через C₁ и мост упадёт до нуля.

Далее, по мере роста сетевого напряжения, напряжение на конденсаторе C₁ будет оставаться неизменным, а напряжение на входе моста будет расти.

В момент времени t₄, когда сетевое напряжение вырастет до значения -(Uca-2Uвых), напряжение на входе моста достигнет значения Uвых, диоды моста откроются и в первичной цепи (через мост и конденсатор C₁) снова потечёт ток. Этот ток снова будет перезаряжать конденсатор C₁, но уже напряжением положительной полярности.

В момент t₆ напряжение на конденсаторе C₁ достигнет максимального значения положительной полярности, а ток через C₁ и мост упадёт до нуля.

Далее весь цикл повторится с самого начала.

Теперь давайте вспомним закон сохранения заряда. В соответствии с этим законом за один полный цикл через конденсатор C₁, мост и нагрузку должно протекать одинаковое количество заряда. Поскольку ток нагрузки у нас постоянный, то количество заряда, протекающего через нагрузку за один цикл, можно найти по формуле Q=Iн*tцикла=Iн/fc, где fc — частота питающего сетевого напряжения. Количество заряда, протекающего через конденсатор C₁, будет равно площади под графиком тока (заштрихованная площадь графика I_C1(t)). Остаётся только найти эту площадь, приравнять её к заряду, протекающему за один цикл через нагрузку, и выразить из полученного выражения необходимую ёмкость конденсатора C₁ в зависимости от тока нагрузки.

Подробные математические расчёты можно найти под вторым спойлером.

[свернуть]

Калькулятор конденсаторов

| Код конденсатора

Код конденсатора

Каждый конденсатор обычно имеет два числа, характеризующих его. Это его емкость и номинальное напряжение . Последний говорит нам о максимальном напряжении, при котором элемент будет работать должным образом. Емкость часто записывается напрямую, поэтому когда вы видите конденсатор с 220 мкФ 25 В , это просто означает, что он имеет емкость 220 мкФ и безопасно работает с напряжениями до 25 В .

Однако, когда емкость ниже 100 мкФ , мы обычно можем найти трехзначный код конденсатора, который определяет значение. Правило простое: Первая и вторая цифры говорят нам о емкости в пФ (пикофарад), а третья — множитель (степень 10) — для числа n , емкость умножается на 10ⁿ . Это просто еще один способ использовать научную нотацию для описания больших чисел.Последняя цифра обычно находится в диапазоне 0-6.

Если имеется одно- или двузначное число, оно просто определяет значение в пФ.

Давайте посмотрим на пример. У нас конденсатор код 104 :

• Первые две цифры говорят о емкости в пФ, что составляет 10 пФ
• Цифра 3ʳᵈ является множителем — 10⁴ или 10,000
• В результате получается 10 пФ * 10⁴ = 10⁵ пФ , или 100 нФ, , или 0.1 мкФ

Мы также можем спросить обратное: Какой код конденсатора для известной емкости? Давайте попробуем с конденсатором с C = 1,24 мкФ :

• Нам нужны две цифры для первых двух цифр кода, поэтому пора округлить значение до двух значащих цифр — 1,24 мкФ → 1,2 мкФ . Таким образом, код будет начинаться с 12 ·
• Чтобы найти последнюю цифру, мы должны использовать соответствующие единицы емкости, пФ — 1.2 мкФ = 1200000 пФ = 12 * 10⁵ пФ
• Из этой формы мы можем сразу определить, что цифра 3ʳᵈ — это 5
• Следовательно, код конденсатора для емкости 1,24 мкФ: 125

К счастью, этот калькулятор конденсаторов работает как в качестве кода емкости , так и в качестве преобразователя емкости в код ! Просто выберите подходящее поле для ввода данных, и результат появится в мгновение ока!

.

Калькулятор конденсаторов

Как работает этот калькулятор конденсаторов?

Это полезный инструмент, который вычисляет общую емкость группы конденсаторов, подключенных последовательно или параллельно. В калькуляторе конденсаторов предусмотрено две вкладки: одна для последовательного расчета, а другая — для параллельного расчета. Все, что вам нужно сделать, это выбрать правильную вкладку, ввести необходимые данные, которые представляют собой значения конденсаторов, разделенные точкой с запятой, после чего инструмент выполнит свою работу.

Последовательная цепь

Это электрическая цепь, в которой ток проходит через все компоненты в этой цепи, потому что компоненты расположены один за другим. Формула для общей емкости группы последовательно соединенных конденсаторов равна сумме отдельных сопротивлений конденсатора:

C всего = 1 / (1 / C1 + 1 / C2 + 1 / C3 … + 1 / Cn)

, где C total — общая емкость, а C — емкость параллельных конденсаторов.

Возьмем для примера схему с 3 последовательно включенными конденсаторами.Последовательные конденсаторы: 15; 7; 10; Суммарная емкость указанной группы конденсаторов в последовательной цепи составляет: 3,23 фарад (Ф)

Параллельная цепь

Это электрическая цепь, в которой компоненты цепи соединены между двумя точками. К каждой точке подсоединяется один из двух концов каждого компонента. Компоненты могут быть простыми элементами ветвей, которые имеют последовательно соединенные элементы.

Формула для общей емкости группы параллельных конденсаторов:

C всего = C1 + C2 + C3… + Cn

, где C total — общая емкость, а C — емкость последовательных конденсаторов.

Пример: схема с 5 параллельными конденсаторами. Параллельные конденсаторы: 4; 5; 6; 8; 9; Суммарная емкость указанной группы конденсаторов, включенных в параллельную цепь: 32,00 фарад (Ф)

Что такое конденсатор?

Это в основном устройство, которое используется для накопления электрического заряда, энергии электростатически в поле. Он состоит как минимум из двух проводников или нескольких пластин, разделенных диэлектриком или изолятором.Впервые он был известен как конденсатор.

26 марта 2015 г.

Калькулятор значения / кода конденсатора

Этот калькулятор значения конденсатора вычисляет значение емкости керамического конденсатора после ввода кода конденсатора в поле ввода ниже.

---

Калькулятор кодов конденсатора

Этот калькулятор кодов конденсатора вычисляет код керамического конденсатора после ввода значения емкости конденсатора в поле ввода ниже.

---

Как работает калькулятор номинала конденсатора / кода?

Поскольку керамические конденсаторы имеют меньшую площадь поверхности из-за их крошечного размера, их значение не записывается в конденсаторе, вместо этого на них записывается закодированный код.Используя этот калькулятор номинала конденсатора, мы можем рассчитать значение этого конденсатора или наоборот. Для электролитических конденсаторов на них просто написаны значения емкости.

Кодировка керамических конденсаторов

Кодировка керамических конденсаторов состоит из 1–3 цифр.

Если код конденсатора состоит только из 1 или 2 цифр, это просто значение их емкости в пикофарадах (пФ). Например, если керамический конденсатор имеет код «5», а другой — «47», их соответствующие значения емкости составляют 5 пФ и 47 пФ.

Для трехзначного кода конденсатора первые две цифры представляют собой значение емкости в пФ, а третья цифра — коэффициент умножения первых двух цифр для расчета окончательного значения емкости конденсатора.

3 ^{-е число} находится в диапазоне от 0 до 6. Оно не может превышать 6.

Если 3 ^число равно 0, это означает коэффициент умножения 1.

Если 3 ^число равно 1, это означает коэффициент умножения 10.

Если 3 ^ряд цифр 2, это означает множитель 100.

Если 3 ^ряд цифра 3, это означает множитель 1000.

Если 3 ^ряд цифр 4, это означает множитель 10000.

Если 3 ^ряд цифр 5, это означает множитель 100000.

Если 3 ^ряд цифра 6, это означает множитель 1000000.

Чтобы понять, как работает умножитель, рассмотрим пример конденсатора с кодом «104».

Поскольку первые две цифры равны 10, а цифра 3 ^{, ряд} — 4, то коэффициент умножения равен 10000, общее значение емкости в пФ будет следующим:

10 * 10000 = 100000 пФ

Аналогичным образом, если код конденсатора равен 152, цифра 3 ^ряд равна 2, поэтому коэффициент умножения равен 100. Значение емкости будет рассчитано следующим образом:

15 * 100 = 1500 пФ

Итак, вот как калькулятор емкости / кода конденсатора вычисляет емкость керамического конденсатора из кода конденсатора, или наоборот.

.

Калькулятор разряда суперконденсатора

Подробнее об этом расчете 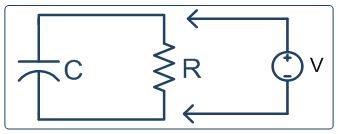Vcapmax — это максимальное значение V CC , до которого заряжается конденсатор. Vcapmin — это минимальное рабочее напряжение, которое вы можете выдержать до того, как ваша схема или компонент, поддерживаемые конденсатором, перестанут работать. Imax — это максимальный ток, при котором ваша цепь разряжает конденсатор.Это может быть постоянный ток или начальный линейный ток при Vcapmax. Значения Imax и Vcap используются для расчета эквивалентного сопротивления цепи, которое используется в уравнение для расчета времени резервного копирования. Рисунок 1. Из базовой электроники формула для определения напряжения на конденсаторе в любой момент времени (для Схема разряда на рисунке 1) составляет: V (t) = E (e -t / RC ) Преобразование этой формулы для времени дает нам: t = — log (V / E) (RC) Где : В — конечное напряжение в вольтах (В) E — начальное напряжение в вольтах (В) R — резистивная нагрузка в омах (Ом) C — емкость конденсатора в фарадах 1F = 1000 000 мкФ = 1000 000 000 нФ = 10000000000000pF t — время в секундах

Подробнее о суперконденсаторах Суперконденсатор, суперконденсатор, псевдоконденсатор, электрохимический двухслойный конденсатор (EDLC) или ультраконденсатор, представляет собой электрохимический конденсатор с относительно высокой плотностью энергии, обычно порядка тысяч раз больше, чем у электролитического конденсатора.Например, электролитический конденсатор типичного размера D-ячейки может иметь емкость в диапазоне десятков миллифарад. Электрический двухслойный конденсатор такого же размера может достигать нескольких фарад, что на два порядка больше. Суперконденсаторы обычно дают более низкое рабочее напряжение в диапазоне 2,5 — 20 В. По состоянию на 2010 год более крупные двухслойные конденсаторы имеют емкость до 5000 фарад. [1] Также в 2010 году самая высокая доступная плотность энергии суперконденсатора на 30 Втч / кг [2] ниже, чем у быстрозаряжаемых литий-титанатных батарей.EDLC имеют множество коммерческих применений, особенно в устройствах «сглаживания энергии» и устройств с мгновенной нагрузкой. Они используются в качестве накопителей энергии в транспортных средствах, а также для небольших приложений, таких как домашние солнечные энергетические системы, где чрезвычайно быстрая зарядка является важной функцией. Суперконденсаторы уже много лет широко используются в качестве резервного источника питания для схем часов реального времени и памяти в микроконтроллерах. Больше информации в Википедии здесь.

.